 |
Формы аналитического описания сигналов
|
|
|
|
Сигналы могут быть представлены во временной, операторной или частотной области, связь между которыми определяется с помощью преобразований Фурье и Лапласа (см. рис.2).
Преобразование Лапласа:
L:  L-1:
L-1:  (8)
(8)
Преобразования Фурье:
F:  F-1:
F-1:  (9)
(9)
L:

L-1:
F-1: p=jw

F: jw=p
Рис.2 Области представления сигналов
При этом могут быть использованы различные формы представления сигналов с виде функций, векторов, матриц, геометрическое и т.д.
При описании случайных процессов во временной области используется, так называемая, корреляционная теория случайных процессов, а при описании в частотной области - спектральная теория случайных процессов.
С учетом четности функций  и
и  и в соответствии с формулами Эйлера:
и в соответствии с формулами Эйлера:
 (10)
(10)
можно записать выражения для корреляционной функции Rx (t) и энергетического спектра (спектральной плотности) случайного процесса Sx (w), которые связанны преобразованием Фурье или формулами Винера - Хинчина
 ; (11)
; (11)
 . (12)
. (12)
Геометрическое представление сигналов и их характеристик
Любые n - чисел можно представить в виде точки (вектора) в n -мерном пространстве, удаленной от начала координат на расстоянии D,
где  . ( 13)
. ( 13)
Сигнал длительностью Tс и шириной спектра Fс, в соответствии с теоремой Котельникова определяется N отсчетами, где N = 2Fc Tc.
|
|
|
Этот сигнал может быть представлен точкой в n - мерном пространстве или вектором, соединяющим эту точку с началом координат [5].
Длина этого вектора (норма) равна:
 ; (14)
; (14)
где xi = x (n Dt) - значение сигнала в момент времени t = n. Dt.
Допустим: X - передаваемое сообщение, а Y - принимаемое. При этом они могут быть представлены векторами (рис.3).
X2,Y2

x2 X
d
y2 Y
g
X1, Y1
0 a 1 a 2 x1 y1
Рис.3. Геометрическое представление сигналов
Определим связи между геометрическим и физическим представлением сигналов. Для угла между векторами X и Y можно записать
cos g = cos (a1- a2) = cos a1 cos a2 + sin a1 sin a2 =
=  ( 15)
( 15)
Для N - отсчетов:
cos g  (16)
(16)
Найдем модуль формального вектора. Для этого рассмотрим кванто-ванный сигнал (рис. 4).
 |
Рис. 4. График сигнала
Рис.4. График сигнала
Средняя мощность сигнала
 .
.
Энергия сигнала
 .
.
Энергия кванта
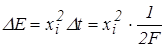 .
.
Энергию квантованного сигнала можно определить по формуле
 .
.
При этом модуль сигнала равен
 .
.
Взаимная корреляционная функция равна
 .
.
При этом
 .
.
Это нормированная корреляционная функция
Если g = 90о, то rxy (t) = 0 - сигналы ортогональны, т.е. независимы;
Если g = 0, то rxy (t) = 1 - передаваемый сигнал равен принятому;
Вектор d - характеризует (помеху) ошибку. Определим дисперсию ошибки:

По вектору ошибки определяют, допустима ли ее величина.
Список литературы
1. Hayes, M. H. Statistical Digital Signal Processing and Modeling. New York: John Wiley & Sons, 1996.
|
|
|
2. Баскаков С.И. Радиотехнические цепи и сигналы: Учеб. для вузов по спец. "Радиотехника". - М.: Высш. шк., 2000.
3. Голд Б., Рэйдер Ч. Цифровая обработка сигналов / Пер. с англ., под ред.А.М. Трахтмана. - М., "Сов. радио", 1973, 368 с.
4. Гринченко А.Г. Теория информации и кодирование: Учебн. пособие. - Харьков: ХПУ, 2000.
5. Карташев В.Г. Основы теории дискретных сигналов и цифровых фильтров. - М.: Высш. шк., 1982.
6. Колесник В.Д., Полтырев Г.Ш. Курс теории информации. -М.: Наука, 1982.
7. Куприянов М.С., Матюшкин Б.Д. - Цифровая обработка сигналов: процессоры, алгоритмы, средства проектирования. - СПб.: Политехника, 1999.
8. Марпл С.Л. Цифровой спектральный анализ. М.: Мир, 1990.
9. Рудаков П. И, Сафонов В.И. Обработка сигналов и изображений Matlab 5. x. Диалог-МИФИ. 2000.
10. Сергиенко А.Б. Цифровая обработка сигналов. - СПб.: Питер, 2002.
|
|
|
12 |


