 |
Однократное замещение в канонических
|
|
|
|
Министерство образования и науки Российской Федерации
Федеральное агентство по образованию
Государственное образовательное учреждение высшего профессионального образования
«Хабаровская государственная академия экономики и права»
Кафедра математики и математических методов в экономике
Математическое программирование
Методические указания к практическим занятиям
для студентов первого курса дневного отделения всех специальностей
Хабаровск 2005
Х12
Математическое программирование: методические указания к практическим занятиям для студентов первого курса дневного отделения всех специальностей / сост. Т. Н. Беспрозванная, Л. А. Дойхен, Е. О. Старкова, С. В. Тонконог. – Хабаровск: РИЦ ХГАЭП, 2005. – 44 с.
В методических указаниях приведены решения типовых задач курса «Линейное программирование», сформулированы алгоритмы основных методов решения, а также осуществлен подбор практических заданий для самостоятельной работы.
В методической разработке предусмотрены задания на составление математических моделей задач линейного программирования, на решение задач линейного программирования основными методами (графический, симплексный и метод искусственного базиса), на составление двойственных задач и последующего их решения, решение транспортных задач как закрытого, так и открытого типов.
Материал соответствует государственным образовательным стандартам по математике для студентов экономических специальностей.
Рецензент к.ф-м.н., доцент кафедры прикладной математики ДВГУПС
Е.Н. Ломакина
Утверждено издательско-библиотечным советом академии в качестве методических указаний
|
|
|
Беспрозванная Татьяна Николаевна
Дойхен Людмила Архиповна
Старкова Елена Олеговна
Тонконог Светлана Владимировна
МАТЕМАТИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
Методические указания к практическим занятиям для студентов первого курса дневного отделения всех специальностей
Редактор Г.С. Одинцова
Подписано в печать 2005г. Формат 60 x 84 / 16. Бумага писчая.
Печать офсетная. Усл.п.л. 2,55. Уч.-изд.л. 1,83. Тираж 550 экз.
Заказ №
__________________________________________________________________________
680042, Хабаровск, ул. Тихоокеанская, 134, ХГАЭП, РИЦ
© Хабаровская государственная академия экономики и права, 2005
ВВЕДЕНИЕ
Проблема оптимизации встречается в различных областях человеческой деятельности, в том числе и в экономике. Поэтому студентам экономических специальностей необходимо освоить методы решения задач линейного программирования.
При огромном разнообразии задач оптимизации только математика может дать общие методы их решения.
В методических указаниях подобраны примеры по всем разделам курса «Линейное программирование»: составление математической модели задач; решение задач линейного программирования графическим и симплексным методами, методом искусственного базиса; решение двойственных задач; транспортные задачи. Подробно разобрано решение типовых задач, что позволит студентам освоить данный курс.
Рекомендуемая литература
1. Дойхен Л. А. Математическое программирование: учеб. пособ. – Хабаровск: РИЦ ХГАЭП, 2001.
2. Кузнецов Ю. А., Кузубов В. И., Волощенко А. Б. Математическое программирование. – М.: Высшая школа, 1980.
3. Красс М. С., Чупрынов Б. П. Математика для экономистов. – СПб.: Питер, 2004.
4. Сборник задач по высшей математике для экономистов: учеб. пособ./ под ред. В. И. Ермакова. – М.: ИНФРА-М, 2002.
5. Тиунчик М. Ф. Руководство к решению задач по линейной алгебре и аналитической геометрии: учеб. пособ. Ч. 1. – Хабаровск: ХГАЭП, 2001.
|
|
|
СОСТАВЛЕНИЕ МОДЕЛИ ЗАДАЧИ ЛИНЕЙНОГО
ПРОГРАММИРОВАНИЯ
Для изготовления четырех видов продукции (А, Б, В, Г) используются три вида сырья  .
.
Ресурсы сырья, нормы его расхода на единицу продукции и получаемая прибыль от единицы продукции заданы в следующей таблице.
| Сырье | Нормы расхода | Ресурсы | |||
| А | Б | В | Г | ||

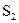

| 7 500 2 800 5 000 | ||||
| Прибыль |
Определить оптимальный план выпуска продукции при условии максимизации прибыли.
Составим математическую модель задачи.
Обозначим через  выпуск продукции А,
выпуск продукции А,  – продукции Б,
– продукции Б,  – продукции В и
– продукции В и  – продукции Г. Следовательно,
– продукции Г. Следовательно,  – план выпуска продукции.
– план выпуска продукции.
Сырья  потребуется в количестве
потребуется в количестве
 .
.
Это количество не должно превышать ресурсы сырья  , т. е.
, т. е.
 .
.
Аналогично по другим видам сырья получим ограничения
 ,
,
 .
.
Подсчитаем прибыль  .
.
Таким образом, мы получили математическую модель, поставленной задачи. Среди решений системы ограничений

необходимо найти такое, при котором целевая функция

достигает максимума.
Составить математические модели следующих задач:
Задача 1. Откорм животных выгоден тогда, когда каждое животное будет получать в дневном рационе не менее 6 единиц питательного вещества А, не менее 12 единиц вещества В и не менее 4 единиц вещества С. Для кормления используются два вида кормов. В таблице указано, сколько единиц каждого питательного вещества содержит 1 кг каждого вида корма.
| Питательные вещества | Корм 1 | Корм 2 |
| А В С |
Цена корма первого вида 5 рублей за 1 кг, второго – 7 рублей. Какое количество корма каждого вида необходимо расходовать ежедневно, чтобы затраты на рацион были минимальными?
Задача 2. При производстве двух видов продукции используются три вида сырья. Необходимо произвести не более 20 единиц продукции первого вида и не более 30 единиц продукции второго вида. Составить план выпуска продукции, обеспечивающий максимальную прибыль. Исходные данные приведены в таблице.
| Запасы сырья | Расход сырья на единицу продукции | |
| 1 вид | 2 вид | |
| Прибыль |
|
|
|
Задача 3. Для выпуска определенного вида продукции могут применяться два технологических способа с различным соотношением ручного и механизированного труда. Ресурсы труда составляют 240 чел.-ч, машинного времени – 120 ч. Их затраты на выпуск единицы продукции первым способом составляют 5 чел.-ч и 2 часа машинного времени. На выпуск единицы продукции вторым способом затрачивается 8 часов рабочего времени и 3 часа машинного времени. Определить такое соотношение технологических способов, которое обеспечит производство максимального количества продукции.
Задача 4. Предприятие может выпускать продукцию трех видов: А, Б, В. Уровень выпуска лимитируется ограниченностью ресурсов – сырья, материалов и оборудования. Затраты на единицу изделия и объем ресурсов указаны в таблице.
| Виды ресурсов | Объем ресурсов | Нормы затрат ресурсов на единицу продукции | ||
| А | Б | В | ||
| Сырье, кг Материалы, кг Оборудование, 1 гр Оборудование, 2 гр | ||||
| Прибыль от единицы продукции |
Определить уровень выпуска продукции, обеспечивающий максимальную прибыль, при условии, что продукции типа В должно быть выпущено не менее 20 изделий.
Задача 5. Консервный комбинат закупает яблоки у двух фермеров. Для производства продукции ему необходимо 100 т яблок первого сорта, 60 т яблок второго сорта и 10 т – третьего сорта. Яблоки закупаются несортированные, но известно, что у первого фермера 70% яблок первого сорта и 30% – второго, у второго фермера 60% яблок первого сорта, 30% – второго и 10% – третьего. Затраты комбината на покупку и перевозку 1 т составляют 8 тыс. руб. для первого поставщика и 6 тыс. руб. для второго. Требуется осуществить закупку и перевозку яблок так, чтобы затраты были минимальными.
Задача 6. Со станции отправляются формируемые здесь пассажирские и скорые поезда. Они отличаются по количеству вагонов разных типов. Количество вагонов каждого типа ограничено. Требуется найти такое соотношение количества пассажирских и скорых поездов, чтобы общее число мест в них было максимальным. Исходные данные по комплектации поездов даны в таблице.
|
|
|
| Типы вагонов | |||||
| багажные | почтовые | плацкартные | купейные | св | |
| Количество вагонов в скором | - | ||||
| Количество вагонов в пассажирском | |||||
| Количество мест в вагоне | - | - | |||
| Количество вагонов на станции |
Задача 7. Грузовая автобаза, обслуживающая пять объектов строительства, развозит песок с трех карьеров суммарной производительностью 700 т песка в сутки (соответственно 250, 300, 150 т). В таблице указано расстояние от карьеров до потребителей (км).
| Карьеры (поставщики) | Объекты строительства (потребители) | ||||
| 1-й карьер 2-й карьер 3-й карьер |
Суточные потребности на объектах соответственно равны 140, 160, 100, 120, 180 т. Составить план перевозок песка, обеспечивающий минимум объема перевозок в тонно-километрах.
Задача 8. Для пошива 120 комплектов изделий на швейной фабрике необходимо иметь заготовки материала в 2,2 м; 1,8 м; 0,7 м. Каждый рулон материала содержит 20 метров. Найти такие способы раскроя материала, чтобы количество использованных рулонов было минимальным (при сохранении комплектности).
Задача 9. Необходимо изготовить 80 комплектов заготовок трех видов длиной в 3 м, 2,4 м и 1,8 м из стержней длиной 7,8 м. Найти способы раскроя и определить, какие из способов раскроя следует выбрать, чтобы число используемых стержней было минимальным.
Задача 10. Для изготовления столов и шкафов употребляют два вида древесины. Расход древесины каждого вида на каждое изделие задан в таблице (в куб. м).
| Изделие | Древесина | Доход от изделия (в руб.) | |
| 1 вид | 2 вид | ||
| Стол Шкаф | 0,15 0,3 | 0,2 0,1 | 2 200 2 500 |
| Количество древесины |
Найти план выпуска изделий, при котором будет получена наибольшая прибыль.
Задача 11. Фирма выпускает два вида мороженого: сливочное и шоколадное. Для изготовления мороженого используются два исходных продукта: молоко и наполнители, расходы которых на 1 кг мороженого и суточные запасы исходных продуктов даны в таблице.
| Исходный продукт | Расход исходных продуктов на 1 кг мороженого | Запас, кг | |
| сливочное | шоколадное | ||
| Молоко | 0,8 | 0,5 | |
| Наполнитель | 0,4 | 0,8 |
Изучение рынка сбыта показало, что суточный спрос на сливочное мороженое превышает спрос на шоколадное не более чем на 100 кг. Кроме того, установлено, что спрос на шоколадное мороженое не превышает 350 кг в сутки. Отпускная цена 1 кг сливочного мороженого 16 ден. ед., шоколадного – 14 ден. ед.
|
|
|
Определить количество мороженого каждого вида, которое должна производить фирма, чтобы доход от реализации продукции был максимальным.
Задача 12. В суточный рацион цыплят включают два продукта питания, П1 и П2, причем продукта П1 должно войти в дневной рацион не более 200 ед. Стоимость 1 ед. продукта П1 составляет 2 ден. ед., продукта П2 – 4 ден. Ед. Содержание питательных веществ в 1 ед. продукта, минимальные нормы потребления указаны в таблице.
| Питательное вещество | Минимальная норма потребления, ед. / день | Содержание питательных веществ в 1 ед. продукта | |
| П1 | П2 | ||
| А | 0,2 | 0,2 | |
| В | 0,4 | 0,2 |
Определить оптимальный рацион питания, стоимость которого будет наименьшей.
Задача 13. «Металлургический завод» из металлов А1, А2, А3 может выпускать сплавы В1, В2, В3. В течение планируемого периода завод должен освоить не менее 640 т металла А1 и 800 т металла А2, при этом металла А3 может быть израсходовано не более 860 т.
Определить минимальные затраты; данные о нормах расхода и себестоимость даны в таблице.
| Вид металла | Технологическая норма расхода металла на условную единицу сплава | Наличие запаса металла у завода | ||
| В1 | В2 | В3 | ||
| А1 | 1,0 | 4,3 | 2,6 | |
| А2 | 5,0 | 1,5 | 3,0 | |
| А3 | 3,0 | 3,9 | 4,3 | |
| Себестоимость 1 т сплава, ден. ед. | - |
Задача 14. Обработка деталей вида А и В может производиться на трех станках. Причем каждая деталь при ее изготовлении должна последовательно обрабатываться на каждом из станков. Прибыль от реализации детали вида А – 100 ден. ед., детали вида В – 160 ден. ед. Исходные данные приведены в таблице.
| Станок | Норма времени на обработку одной детали, ч | Время работы станка, ч | |
| А | В | ||
| 0,2 | 0,1 | ||
| 0,2 | 0,5 | ||
| 0,1 | 0,2 |
Определить производственную программу, максимизирующую прибыль при условии: спрос на деталь вида А не менее 300 шт., на деталь вида В – не более 200 шт.
Задача 15. Ткань трех артикулов производится на ткацких станках двух типов с различной производительностью. Для изготовления тканей используются пряжа и красители. В таблице указаны мощности станков в тысячах станко-часах, ресурсы пряжи и красителей в 1000 кг, производительности станков в метрах за час, нормы расхода пряжи и краски в кг на 1000 м и цена 1 м ткани.
| Вид ресурса | Объем ресурсов | Норма расхода | ||
| Станки 1-го типа | ||||
| Станки 2-го типа | ||||
| Пряжа | ||||
| Красители | ||||
| Цена, ден. ед. | - |
Определить оптимальный ассортимент, максимизирующий объем товарной продукции предприятия.
МЕТОД ЖОРДАНА – ГАУССА.
ОДНОКРАТНОЕ ЗАМЕЩЕНИЕ В КАНОНИЧЕСКИХ
СИСТЕМАХ
Решение системылинейных алгебраических уравнений приводится в таблице Гаусса согласно алгоритму метода последовательных исключений:
1) каждая последовательная итерация начинается с выбора разрешающего элемента, отличного от нуля, в предыдущей таблице (удобно в качестве разрешающего элемента выбирать элемент, равный 1);
2) элементы разрешающей строки делим на разрешающий элемент;
3) элементы разрешающего столбца, не принадлежащие разрешающей строке, заполняем нулями;
4) элементы остальных строк пересчитываем по «правилу прямоугольника»:

| 
| |

| ||

| 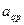
|
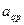 – разрешающий элемент.
– разрешающий элемент.
Тогда элемент  вычисляется по формуле
вычисляется по формуле
 .
.
Алгоритм применяется до тех пор, пока в каждой строке не получим базисные переменные.
Пример 1. Решить систему методом Жордана – Гаусса. Если система имеет множество решений, найти хотя бы одно базисное и указать, будет ли оно опорным.

Решение:
| Б | 
| 
| 
|  
| 
|
| -1 | -2 | -2 | |||

|  2
-1
-4 2
-1
-4
| -9 -36 | -4 -17 | -8 -32 | |


| -11 | -5
 4
-1 4
-1
| -10 | ||


| -11 | -10 |
Систему привели к системе с базисом:

Базисное решение  не является опорным.
не является опорным.
Пример 2. Дана каноническая система:

где  – базисные неизвестные, свободные члены неотрицательны. Если свободные неизвестные
– базисные неизвестные, свободные члены неотрицательны. Если свободные неизвестные  прировнять к нулю, то получим базисное неотрицательное решение, которое называется опорным.
прировнять к нулю, то получим базисное неотрицательное решение, которое называется опорным.
Итак,  – опорное решение.
– опорное решение.
Для нахождения других опорных решений выполняем операцию однократного замещения, при этом:
1) разрешающий столбец выбираем так, чтобы в нем оказался хотя бы один положительный элемент;
2) разрешающую строку выбираем по наименьшему Ө, который равен отношению свободных членов к положительным элементам разрешающего столбца.
| Б | 
| 
| 
| 
| 
| 
| Ө |

|
 3 3
| -3 -2 | 2/1=2 1/3 - | ||||

| -3 1/3 | -10/3 1/3 -2 | 5/3 1/3 |
 – опорное решение.
– опорное решение.
Можно найти и другие опорные решения, например, в качестве разрешающего столбца можно выбрать столбец соответствующий  .
.
Решить системы методом Жордана – Гаусса. Если система имеет множество решений, найти базисное.
1.  2.
2. 
3.  4.
4. 
5. 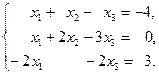 6.
6. 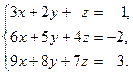
7.  8.
8. 
Найти все опорные решения следующих систем.
9.  10.
10. 
11.  12.
12. 
13.  14.
14. 
15.  16.
16. 
ГРАФИЧЕСКИЙ МЕТОД
Графически решаются задачи в стандартной форме, содержащие не более двух переменных; задачи общего вида, в системе ограничений которых не более двух свободных неизвестных.
Рассмотрим примеры.
Пример 1. Решить графически задачу линейного программирования.


Строим область решений системы ограничений. Для этого последовательно определяем области решений каждого неравенства.
Чтобы найти область решений первого неравенства, строим граничную прямую  , которая делит плоскость на две полуплоскости, а затем, испытывая какую-либо точку (проще О(0;0)), определяем полуплоскость, точки которой удовлетворяют неравенству. Точка О(0;0) не удовлетворяет неравенству
, которая делит плоскость на две полуплоскости, а затем, испытывая какую-либо точку (проще О(0;0)), определяем полуплоскость, точки которой удовлетворяют неравенству. Точка О(0;0) не удовлетворяет неравенству  , следовательно, область решений неравенства не включает начала координат. Отмечаем область стрелками.
, следовательно, область решений неравенства не включает начала координат. Отмечаем область стрелками.
Решаем аналогично остальные неравенства, находим общую область решений, удовлетворяющую всем неравенствам.

Областью решений системы неравенств является многоугольник АВСДЕМ. Так как решения удовлетворяют условиям  , область решений называется допустимой областью решений задачи.
, область решений называется допустимой областью решений задачи.
В этой же системе координат строим целевой вектор  , перпендикулярный к линиям уровня
, перпендикулярный к линиям уровня  . Строим перпендикулярно вектору линию уровня и, перемещая ее параллельно самой себе в направлении вектора
. Строим перпендикулярно вектору линию уровня и, перемещая ее параллельно самой себе в направлении вектора  , определим крайнюю точку области, в которой Z примет наибольшее значение.
, определим крайнюю точку области, в которой Z примет наибольшее значение.
В решаемой задаче максимальное значение Z будет достигнуто в точке Е. Определяем координаты этой точки:
 Е(6; 2),
Е(6; 2),

 .
.
Пример 2. Решить графически:


Приводим систему к системе с базисом:
| Б | 
| 
| 
| 
| 
|
 1 1
| -1 | ||||

| -2 |
 2 2
| |||

| -1 |

Перейдем от канонической системы к стандартной, отбрасывая в уравнениях базисные переменные.

Исключаем базисные переменные из выражения для функции Z

 .
.
Решаем графически задачу:
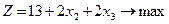


Максимальное значение функции Z достигается в точке А(4;0):
 .
.
Найдем оптимальное значение  :
:
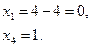
Ответ:  .
.
Решить графически следующие задачи линейного программирования:
1.  2.
2. 


3.  4.
4. 
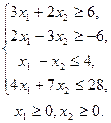

5.  6.
6. 


7.  8.
8. 


9.  10.
10. 
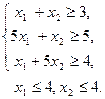

11.  12.
12. 

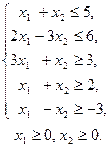
13. 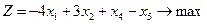 14.
14. 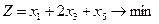

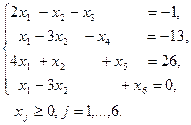
15. Изготовление продукции двух видов требует использования сырья трех видов. Запасы сырья, норма расхода и прибыль от реализации единицы продукции приведены в таблице:
| Вид сырья | Запас сырья | Норма расхода | |

| 
| ||

| |||
| Доход от реализации одного изделия |
Составить план производства, обеспечивающий наибольшую прибыль.
16. Человек должен потреблять в сутки некоторое количество питательных веществ. Их содержание в разных видах пищи приведено в таблице:
| Питательные вещества | Норма | Виды пищи | |
| А | Б | ||
| Жиры Белки Углеводы | |||
| Стоимость 1 усл. ед. вида пищи |
Составить диету наименьшей стоимости при условии, что организм должен получить минимальную суточную норму питательных веществ. пт. е. ять к нулю, то ные ободные члены не отрицат
СИМПЛЕКСНЫЙ МЕТОД
Если система ограничений основной задачи каноническая, то задачу линейного программирования можно решить симплексным методом.
Пример 1. Решим задачу симплекс-методом:

Преобразуем стандартную задачу в основную, добавляя к левым частям ограничений балансовые переменные. Целевая функция при этом не изменится.

Получим каноническую задачу. Неизвестные  – базисные,
– базисные,  – свободные. Можно записать исходное опорное решение:
– свободные. Можно записать исходное опорное решение:  .
.
Составим симплексную таблицу:
| Cj базиса | Базис | C1=1 | C2=6 | C3=0 | C4=0 | C5=0 | θ | |

| 
| 
| 
| 
| 
| |||



| -2 |
-2
 1 1
| - | |||||
 = =
| -1 | -6 | ||||||



|  3
-3
-2 3
-3
-2
| -1 | 2/3 - - | |||||
 = =
| -13 | |||||||



| 2/3 16/3 | 1/3 2/3 | -1/3 1/3 | |||||
 = =
| 98/3 | 13/3 | 5/3 |
Cj – коэффициенты целевой функции. При х1 коэффициент C1=1, при х2 – C2=6, неизвестные х3, х4, х5 отсутствуют в целевой функции, следовательно их коэффициенты равны нулю. В первом столбце таблицы записываются коэффициенты целевой функции, соответствующие базисным неизвестным второго столбца таблицы.
Алгоритм симплекс-метода
1. Записываем данную задачу в исходную симплекс-таблицу.
2. Если все элементы оценочной строки симплексной таблицы неотрицательны, то исходный план является оптимальным.
3. Если в оценочной строке содержится отрицательный элемент, над которым в таблице нет положительных элементов, то целевая функция не ограничена сверху и задача не имеет решения.
4. Если над каждым отрицательным элементом оценочной строки в соответствующем столбце есть хотя бы один положительный элемент, то можно перейти к лучшему плану.
С этой целью:
а) выбираем в исходной таблице разрешающий столбец. Это столбец, соответствующий наименьшей отрицательной оценке. Пусть это столбец, соответствующий переменной  ;
;
б) выбираем разрешающую (q-тую) строку из условия

в) элемент 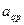 – разрешающий;
– разрешающий;
г) элементы разрешающей строки делим на разрешающий элемент;
д) элементы остальных строк вычисляем по правилу «прямоугольника»;
е) элементы оценочной строки также вычисляются по правилу нахождения оценок. Эту формулу можно использовать в качестве контроля вычислений.
Правило нахождения оценок
Оценка для хj равна сумме произведений элементов данного столбца на соответствующие элементы первого столбца (Сj-базисные) минус Сj данного столбца (коэффициент над хj).
Например, в первой части таблицы оценка при х2 равна:
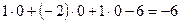 ,
,
в третьей части таблицы оценка при х3 равна:
 .
.
Значение целевой функции при данном базисе подсчитывается по правилу нахождения оценок. Так, в третьей части таблицы
 .
.
При решении задачи на максимум опорный план будет оптимальным, если все оценки будут неотрицательными. Исходный опорный план 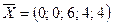 не будет оптимальным, т.к. оценки при х1 и х2 – отрицательные.
не будет оптимальным, т.к. оценки при х1 и х2 – отрицательные.
По наименьшей отрицательной оценке выбираем разрешающий столбец (столбец х2). Можно перейти к лучшему опорному плану методом однократного замещения, если в этом столбце есть хотя бы один положительный элемент. В нашем примере это условие выполняется. Теперь необходимо выбрать разрешающую строку.
Разрешающую строку определяем по наименьшему θ, равному отношению свободных членов ( ) к соответствующим положительным элементам разрешающего столбца. В разрешающем столбце х2 два положительных элемента. Находим отношения:
) к соответствующим положительным элементам разрешающего столбца. В разрешающем столбце х2 два положительных элемента. Находим отношения:

Наименьшим отношением является отношение  , следовательно,
, следовательно, 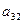 =1 – разрешающий элемент. Неизвестное х2 входит в базис вместо х5. Т.о. посредством преобразования однократного замещения мы перешли к лучшему опорному плану
=1 – разрешающий элемент. Неизвестное х2 входит в базис вместо х5. Т.о. посредством преобразования однократного замещения мы перешли к лучшему опорному плану  , при котором
, при котором  . Но этот план также не является оптимальным, т.к. при х3 оценка отрицательная. В третьей части таблицы получен оптимальный план (нет отрицательных оценок):
. Но этот план также не является оптимальным, т.к. при х3 оценка отрицательная. В третьей части таблицы получен оптимальный план (нет отрицательных оценок): 
Замечание 1. Оценки и значение целевой функции, начиная со второй части таблицы, следует для контроля считать и по правилу нахождения оценок, и по правилу прямоугольника.
Замечание 2. Если в столбце с отрицательной оценкой нет положительных элементов, то задача оптимального решения не имеет, а целевая функция на множестве допустимых решений неограниченна ( ).
).
Замечание 3. Если требуется найти минимум функции
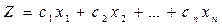 ,
,
то можно перейти к задаче максимизации функции
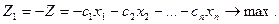
Замечание 4. Приз
|
|
|


