 |
Метод искусственного базиса
|
|
|
|
(М-задача)
Метод искусственного базиса применяется при решении задач линейного программирования, системы ограничений которых не являются каноническими.
Рассмотрим задачу в общем виде:
(1)
(2)
Пусть система (1) не является системой с базисом. Прибавим к левой части каждого уравнения системы (1) переменную уi ≥ 0, которую назовем искусственной. Система примет вид:
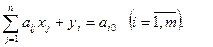(3)
(3) – система с базисом.
Составим новую целевую функцию:
(4)
Задача нахождения максимума функции (4) при ограничениях (3) называется М-задачей.
Замечание 1. Если исходная задача решается на минимум, то целевая функция М-задачи составляется так:
В обоих случаях М может принимать сколь угодно большое положительное значение.
Замечание 2. Искусственные неизвестные следует вводить только в те ограничения, которые не содержат базисных неизвестных.
Связь между решениями исходной и М-задачей устанавливается следующими теоремами.
Теорема 1. Если в оптимальном плане 
М-задачи все искусственные переменные равны нулю, то соответствующее решение 
исходной задачи также является оптимальным.
Теорема 2. Если в оптимальном плане М-задачи хотя бы одна из искусственных переменных отлична от нуля, то исходная задача решения не имеет.
Алгоритм метода искусственного базиса имеет свои особенности:
1) симплексная таблица имеет две оценочные строки: М-строку и Z-строку. Оценка в М-задаче имеет вид: а + bМ, где М > 0 сколь угодно большое число. Следовательно, знак оценки определяется знаком коэффициента b. Число а записываем в Z-строку (первую строку оценки), а коэффициент b – в М-строку (вторую строку);
2) разрешающий столбец выбирается по оценкам М-строки;
|
|
|
3) если все искусственные переменные вышли из базиса, задача решается дальше обычным симплекс-методом;
4) если М-задача решена, но искусственные переменные не вышли из базиса, то исходная задача решения не имеет.
Пример 1.
Преобразуем систему ограничений к системе уравнений:
Второе и третье ограничения не содержат базисных неизвестных, поэтому мы добавляем искусственные переменные именно в эти уравнения:
Целевая функция М-задачи:
Составляем симплексную таблицу:
| Сj | Б | -1 | θ | |||||
| 
| 
| 
| 
| 
| |||
|
|
 5
| -1 | 5/2 1/5 | ||||
 
| -5 | -2 | ||||||
| -7 | -8 | -5 | -5 | ||||
|
|
| 23/5 27/5 1/5 | -1/5 1/5 3/5 | -3/5 -7/5 4/5 |  2/5
3/5
-1/5
| 23/2 27/3 - | ||
|
| -1 | |||||||
|
| -27/5 | -1/5 | 7/5 | -3/5 | ||||
|
| -1/3 1/3 2/3 | 1/5 -7/5 1/3 | ||||||
|
| 4/3 | 8/3 |
Оптимальный план: 
Замечание. Как только искусственные переменные выходят из базиса, элементы М-строки обращаются в ноль, и в дальнейшем М-строка из рассмотрения исключается.
Пример 2.
Вводим балансовые переменные:
Система не каноническая.
Составляем М-задачу:
Решаем М-задачу симплексным методом:
| Сj | Б |
| θ | ||||
|
|
|
|
| ||||
|
|
|  1
| -1 | ||||
|
| -2 | -3 | |||||
|
| -6 | -3 | -2 | ||||
|
|
| -1 | -3 | -1 | |||
|
| -1 | ||||||
|
| -3 |
М-задача решена (нет отрицательных оценок в М-строке), но в этом решении искусственная неизвестная y осталась в базисе, следовательно, исходная задача не имеет оптимального решения, так как область допустимых решений этой задачи пустая.
Решить следующие задачи:
1. 
3. 
5. 
7. 
|
|
|
9.
11. 
2. 
4. 
6. 
8. 
10. 
12. 
13. 
15. 
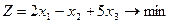
14. 
16. 
ДВОЙСТВЕННОСТЬ
Пример 1. Рассмотрим задачу об оптимальном плане выпуска продукции: для изготовления 4 видов продукции используется 2 вида сырья. Запасы сырья и его расход на изготовление единицы каждого вида продукции даны в таблице:
| Виды сырья | Запасы | Виды продукции | |||
| I | II | III | IV | ||
| А Б | - | ||||
| Доход |
Определить оптимальный план выпуска продукции из условия максимизации прибыли.
Математическая формулировка (модель) задачи:
Максимизировать функцию
при ограничениях
Предположим, что некоторая организация желает приобрести сырье, которым располагает предприятие. Надо оценить каждую единицу, используемых ресурсов. Будем такую оценку условно называть ценой.
Обозначим соответственно, через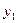 
и 
цену единицы сырья А и Б.
Производство продукции вида I приносит предприятию доход 12 денежных единиц. При этом расходуется 4 единицы сырья А и 0 единиц сырья Б. Выручка от продажи сырья, расходуемого на единицу продукции I по ценам 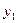и , составит
.
Эта величина должна быть не меньше тех доходов, которые предприятие получит от реализации продукции вида I, следовательно,
.
Аналогичные рассуждения в отношении единицы продукции вида II, III, IV приводят к следующим неравенствам:
Общая стоимость всех запасов сырья, приобретаемого организацией, составит 
.
Покупатель будет стремиться купить сырье как можно дешевле, т.е. минимизировать функцию 
.
Получим задачу:
Получили задачу, двойственную данной. Следовательно, для стандартной задачи нужно выполнить следующие действия, для того чтобы получить ей двойственную:
1) число неизвестных в двойственной задаче равно числу ограничений в исходной;
2) неравенства в системе ограничений двойственной задачи будут противоположного смысла, чем неравенства в системе ограничений исходной задачи; сохраняется неотрицательность переменных;
3) свободные члены ограничений исходной задачи становятся коэффициентами целевой функции двойственной задачи, а коэффициенты целевой функции исходной задачи превращаются в свободные члены двойственной задачи;
|
|
|
4) в исходной задаче целевая функция минимизируется, а в двойственной – максимизируется.
По решению одной из задач можно сразу определить решение другой.
Решим исходную задачу симплекс-методом:
| Сj | Б | θ | |||||||
|
|
|
|
|
|
| 
| |||
|
|  4
| - | |||||||
| =
| -12 | -5 | -4 | -1 | |||||
|
| 3/4 |  1/4
| 1/4 | 1/4 | |||||
| =
| -1 | ||||||||
|
| 23/36 4/9 | -1/12 4/3 | 1/4 | -1/36 1/9 | |||||
| =
| 40/9 | 10/3 | 1/9 | ||||||
|
|
|
.
Следовательно, для двойственной задачи
.
Неизвестные в двойственной задаче равны соответствующим оптимальным оценкам базисных переменных исходной задачи плюс коэффициент, стоящий в таблице над соответствующей базисной переменной (Сj), т.е. 
.
Проверим:
.
При 
, 
.
Пример 2. В двойственной задаче к основной переменные могут иметь любой знак. Составим двойственную задачу к основной:
Двойственная задача имеет следующий вид:
Решим двойственную задачу графически
 |
Координаты точки А дают значения неизвестных и , при которых функция принимает минимальное значение.
Найдем координаты этой точки:
По решению двойственной задачи найдем решение исходной по второй теореме двойственности (теореме равновесия).
Подставим координаты точки 
в систему ограничений двойственной задачи:
Получим:
Первое неравенство выполняется как строгое неравенство, следовательно, соответствующая переменная 
исходной задачи равна 0. Последние два неравенства обращаются в равенства, следовательно, соответствующие им переменные > 0.
Решая систему:
получим ответ для исходной задачи: 
.
В следующих примерах составить двойственную задачу к данной. Одну из задач решить и найти оптимальное решение другой задачи (по основной теореме двойственности; по теореме равновесия).
1.
3. 
5. 
|
|
|
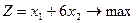
2.
4. 
6. 
7. 
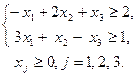
9. 
11. 
13. 
15. 
8.
10. 
12.
14.
16. 
ТРАНСПОРТНАЯ ЗАДАЧА
Классическая транспортная задача – задача о наиболее экономном плане перевозок однородного продукта или взаимозаменяемых продуктов из пунктов отправления в пункты назначения.
На m станциях отправления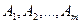 
сосредоточенно соответственно 
единиц некоторого однородного груза. Этот груз следует перевезти в n пунктов назначения 
, причем в каждый из них надлежит завезти соответственно 
единиц этого груза.
Известны транспортные издержки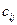 
, связанные с перевозкой единицы груза из пункта 
.
Требуется составить такой план перевозок, при котором сумма транспортных издержек окажется минимальной.
Рассмотрим закрытую модель, т. е. будем рассматривать задачи в которых суммарные запасы грузов у поставщиков равны суммарным потребностям потребителей:
.
Составим математическую модель задачи.
Ограничения по ресурсам:
Ограничения по потребителям:
Условия неотрицательности:
Целевая функция:
Транспортную задачу решают методом потенциалов, но применить его можно только в том случае, когда найден какой-то план задачи. Существует несколько методов нахождения исходного допустимого решения (плана): метод «северо-западного» угла, метод минимального тарифа.
Метод «северо-западного» угла
Не учитывая стоимости перевозки единицы груза, начинаем заполнение таблицы с удовлетворения потребностей первого потребителя 
за счет запаса поставщика 
. Затем удовлетворяем потребности потребителя 
, и так далее, пока все потребители не будут удовлетворены, а поставщики разгружены.
Метод минимального тарифа
Выбираем клетку с наименьшим тарифом 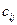; записываем в клетку максимально возможную поставку.
При этом могут встретиться три случая:
В первом случае потребности 
удовлетворятся полностью запасами поставщика 
. Столбец исключаем из рассмотрения.
Во втором исключаем строку 
, записав в клетку 
.
В третьем принимаем 
. Затем записываем ноль в следующую по строке или столбцу клетку и исключаем и пункт 
.
На каждом шаге таблица сокращается, и в итоге получим допустимый план задачи.
Замечание 1. В транспортной таблице занятые клетки соответствуют базисным неизвестным, а пустые клетки свободным неизвестным. Число базисных неизвестных в системе ограничений транспортной задачи равно m+n-1, где m – число поставщиков, n – число потребителей.
|
|
|
