Аэродинамика (механика газа)

 

Аэродинамикой называется раздел механики жидкости и газа, изучающий закономерности покоя и движения газов.

В области строительства аэродинамические расчёты связаны главным образом с воздухом, на который в основном и будем ориентироваться в данной книге.

Многие гидравлические принципы сохраняются и для газов, так как последние часто считают условно несжимаемыми, как и жидкости. Поэтому в аэродинамике много ссылок на гидравлику.

Положения аэродинамики используются для расчёта систем вентиляции и газоснабжения зданий, при определении ветровых нагрузок на строительные конструкции, в расчётах продуваемости жилых микрорайонов, для оценки воздухопроницаемости стен и оконных проёмов зданий.

 

Физические свойства газов

 

Определения плотности r, удельного веса g, вязкости динамической m и кинематической n, приведённые для жидкости в гидравлике (см. с. 8-9), остаются в силе и для газа.

 

Плотность

 

Плотность газа r (кг/м ³) в зависимости от давления и температуры можно рассчитать по формуле Менделеева и Клапейрóна

(55)

где p_ст — статическое давление в газе, Па (аналогично гидростатическому — см. с. 10); R_г — газовая постоянная, Дж /(кг · K); T — абсолютная температура газа в градусах Кéльвина (К), вычисляемая через температуру t ° в градусах Цельсия (° C) по формуле

T = t °+273°. (56)

Например, плотность воздуха при t ° = +20 ° C, нормальном атмосферном давлении p_ст = p_атм = 101325 Па и соответствующей газовой постоянной R_г = 287 Дж/ (кг · K) будет по формуле (55)

r = 101325 / (287 (20 + 273)) = 1,2 кг/м ³.

В расчётах воздухообмена в зданиях плотность воздуха определяют упрощённо при условии постоянства давления (изобарный процесс): p_ст = p_атм = 101325 Па. При этом плотность воздуха r считают зависящей только от его температуры Т. В дальнейшем, будем иметь в виду только такую простейшую зависимость.

 

Удельный вес

 

Удельный вес газа g (Н/м ³) находится по формуле:

g = r g. (57)

 

Вязкость

 

Динамическая вязкость воздуха m (Па·с) может быть определена по экспериментальной формуле Р.Э. Мúлликена

m = 1,745·10^-5 + 5,03·10^-8 t °. (58)

где t ° — температура, ° C. Например, при t ° = +20 °C вычисляем динамическую m = 1,85·10^-5 Па · с и кинематическую вязкость n = m / r = = 1,85·10^-5 / 1,2 = 1,54·10^-5 м ² /с.

Обратим внимание, что с увеличением температуры вязкость газа увеличивается (и, наоборот, с уменьшением — уменьшается), в отличие от жидкостей, которые при нагревании становятся менее вязкими (см. с. 9).

 

Статика газа

 

Статика газа — это раздел аэродинамики (механики газа), изучающий законы равновесия покоящегося газа и распределения в нём давления.

 

Статическое давление

 

Статическое давление p_ст (Па), действующее в покоящемся газе, складывается из внешнего давления на газ p ₀ на некотором горизонтальном уровне (например, замеренное барометром атмосферное давление) и давления собственного веса газа (весового давления) (рис. 23):

p_ст = p ₀ + g h = p ₀ + r g h, (59)

где h — высота слоя газа над точкой, в которой определяется статическое давление. Приведённое уравнение аналогично основному уравнению гидростатики (см. с. 10). Оно показывает, что давление в газе, как и в жидкости, с изменением высоты меняется по линейной зависимости.

 

Приборы для измерения давления

 

Для измерения давления в газе могут применяться следующие приборы:

— барометры (измеряют атмосферное давление);

— манометры (измеряют избыточное давление);

— вакуумметры (измеряют вакуум — см. с. 12).

Давление в газе в системе СИ измеряется в паскалях (Па = Н/м ²), которые связаны с миллиметрами водяного столба и кгс/см ² так:

1 Па = 0,1 мм вод.ст. = 10^-5 кгс/см ².

В атмосферном воздухе статическое давление p_ст равно атмосферному p_атм на уровне, где оно измеряется барометром. Для других уровней делают поправку r g h c плюсом или минусом. Например, в атмосфере при t ° = +20 ° C давление при подъёме на каждые восемь метров уменьшается примерно на 100 Па — это можно проверить по формуле (59) для p_ст.

При измерении p_ст в резервуарах (рис. 24) различают два случая:

1. Когда внутри давление больше атмосферного (p_ст › p_ман), то используются барометр и манометр и тогда

p_ст = p_атм + p_ман,

где p_ман — давление манометрическое (избыточное).

2. Когда внутри давление меньше атмосферного (p_ст ‹ p_атм), то используются барометр и вакуумметр и тогда

p_ст = p_атм + p_в,

где p_в — давление вакуумметрическое (см. с. 12).

 

Эпюры давления

 

Для расчёта на прочность замкнутых конструкций, ограждающих газ (трубопроводов, баллонов, резервуаров, газгольдеров и т.д.), на их поверхностях строят эпюры давления:

— избыточного p_ман = p_ст – p_атм (рис. 25,а);

— вакуумметрического p_в = p_атм – p_ст (рис. 25,б).

Эпюры давления на рис. 25 построены с пренебрежением изменения давления по высоте резервуара, поэтому на вертикальных стенках они прямоугольные, а не треугольные как для жидкости (см. рис. 5). Такой приём допускается для газа при небольших высотах из-за малости его удельного веса. Эпюры давления служат исходными данными для расчёта конструкций на прочность методами сопромата и строительной механики.

Приведённое статическое давление

 

Статическое давление p_ст не выражает условия равновесия (покоя) газа. Например, газ покоится, но по высоте z в разных его точках величина p_ст разная, так как z является переменной. В гидравлике применяют понятие гидростатического напора H (см. с. 15), который для всех точек покоящейся жидкости одинаков. Однако для газа напор не удобно вводить из-за переменной плотности r, зависящей от температуры. Поэтому в газе для энергетического сравнения его точек удобно использовать понятие приведённого статического давления (рис. 26):

p_пр.ст = r g z + p_ст, (60)

где r g z — давление положения точки газа, отстоящей на высоту z от нулевой горизонтальной плоскости отсчёта 0-0; r — плотность газа, соответствующая температуре в рассматриваемой точке. То есть p_пр.ст приводит давления газа в различных точках к одному уровню 0-0.

 

Условие равновесия газа можно сформулировать так: если приведённые статические давления p_пр.ст в различных его точках одинаковы, то газ покоится.

Это легко доказывается, например, по рис. 26 и формулам (60) и (59) для двух точек газа А и В. Значения p_пр.ст для точек А и В равны, значит газ находится в состоянии покоя, без движения.

Динамика газа

 

Динамика газа — это раздел аэродинамики (механики газа), изучающий закономерности движущихся газов (потоков газов). Будем рассматривать, главным образом, воздух.

На практике движение воздуха подобно движению несжимаемой жидкости (как в гидравлике). Разница состоит лишь в физических свойствах (плотности r, вязкости n) и в использовании для газа величин давления вместо напора.

 

Словарь аэродинамических терминов

 

Аэродинамическую терминологию приведём в сопоставлении с гидравлической.

Аналогия напорным и безнапорным потокам жидкости существует и в газах.

Поток газа в трубопроводе, закрытом канале или воздуховоде заполняет сечение полностью, соприкасаясь со стенками, поэтому он аналогичен напорному. Такие потоки, например, наблюдаются в системах вентиляции, а также в газопроводах.

Аналогию с безнапорными потоками можно проследить в так называемых свободных струях. Например, в струях тёплого воздуха — воздушных завесах, устраиваемых зимой при входе в общественные здания.

В аэродинамике определения площади живого сечения w, м ², расхода потока Q, м ³ /с, скорости потока V, м/с, можно использовать гидравлические (см. гидродинамику, с. 16), заменив слово «жидкость» на «газ». Величины скоростей в сетях вентиляции и отопления зданий обычно лежат в пределах 0,5—1,5 м/с.

Для трубопроводов, каналов и воздуховодов круглого сечения расчётным геометрическим параметром является внутренний диаметр d. Если сечение некруглое, то его приводят к условно круглому с эквивалентным диаметром d_э по формуле

d_э = 4 w / c, (61)

причём c — полный периметр сечения (как для напорной трубы).

Например, для воздуховода прямоугольного сечения со сторонами a и b эквивалентный диаметр находится так:

d_э = 4 w / c = 2 a b / (a + b).

Уравнение неразрывности потока

 

Уравнение неразрывности потока газа, отражающее физический закон сохранения массы, выглядит так:

V ₁ w ₁ = V ₂ w ₂, (62)

то есть точно так же, что и для жидкости (см. с. 18), и с тем же следствием: при уменьшении площади живого сечения скорость потока увеличивается, и наоборот.

 

Приведённое полное давление

 

В любой точке движущегося газа действует полное давление

p_п = p_ст + p_д, (63)

где p_ст — статическое давление (см. с. 42); p_д = r V ²/2—динамическое давление, отражающее кинетическую энергию потока газа (аналогично скоростному напору в жидкости h_V = V ² / (2 g) — см. с. 19).

Однако величина полного давления p_п не охватывает полную энергию точки движущегося газа, так как в ней не содержится давление положения точки r g z. Поэтому в качестве энергетической характеристики любой точки потока газа введём понятие приведённого полного давления (рис. 27):

p_пр.п = r g z + p_ст + r V ²/2, (64)

где первые два члена r g z + p_ст представляют собой потенциальную часть энергии, а последний r V ² / 2 — кинетическую.

 

Уравнение Бернулли для газа

 

Рассмотрим поток газа, проходящий по трубопроводу переменного сечения (рис. 28). В первом сечении приведённое полное давление равно p_{пр.п 1}. При прохождении по трубе часть p_{пр.п 1} необратимо потеряется из-за проявления сил внутреннего трения газа и во втором сечении энергетическая характеристика уменьшится до p_{пр.п 2} на величину потерь давления D p_пот.

Уравнение Бeрнýлли для газа в простейшем виде записывается так:

p_{пр.п 1} = p_{пр.п 2}+ D p_пот, (65)

то есть оно аналогично уравнению Бeрнýлли для жидкости (21) на с. 20, но записано в давлениях, а не напорах.

Уравнение Бeрнýлли в традиционной записи получим, если в последнем равенстве раскроем значения приведённых полных давлений p_{пр.п 1} и p_{пр.п 2} по (64):

(66)

Энергетический смысл уравнения Бeрнýлли для газа заключается в том, что оно отражает закон сохранения энергии, а геометрический не рассматривается, так как величины в нём выражаются в единицах давления (Па), а не напора (м).

 

Разность давлений и потери давления

 

Движение газа происходит только при наличии разности приведённых полных давлений D p_пр = p_{пр.п 1} – p_{пр.п 2} от бóльшего давления p_{пр.п 1} к меньшему p_{пр.п 2}. Например, так работает естественная вентиляция для удаления воздуха из помещений зданий.

Потери давления D p_пот отражают потерю полной энергии потока при движении газа. Например, чем длиннее воздуховод, меньше его проходное сечение, шероховатее его стенки, тем больше будут потери давления D p_пот в системе вентиляции, что может ухудшить удаление несвежего воздуха из помещений.

При установившемся движении газа разность давлений численно равна потерям давления: D p_пр = D p_пот .

Таким образом, «разность давлений» является причиной движения газа, а «потери давления» — следствием. Измеряются они в одних и тех же единицах СИ — паскалях (Па).

 

Режимы движения газа

 

При проведении аэродинамического расчёта в первую очередь нужно выяснять, какой режим движения будет наблюдаться у данного потока газа.

Режимы движения газовых потоков делятся на два типа (так же, как в жидкостях):

1) ламинарный, спокойный, при малых скоростях;

2) турбулентный, вихреобразный, при больших скоростях.

Для выяснения типа режима нужно рассчитать число Рéйнольдса Re и сравнить его с критическим числом Re _кр для газа.

Число Рéйнольдса для газа Re вычисляют по формуле:

Re = V d_э /n, (67)

где d_э — эквивалентный диаметр трубопровода, воздуховода или канала (см. с. 46); d_э = d, если трубопровод круглого сечения.

Критическое число Рейнольдса для газа Re _кр» 2000.

Если Re ‹ Re _кр, то режим ламинарный.

Если Re › Re _кр, то режим турбулентный.

На практике в подавляющем большинстве случаев наблюдается режим турбулентный: в вентиляционных каналах (воздуховодах), газопроводах, паропроводах, при ветре.

Аэродинамика инженерных сетей

 

Инженерные сети вентиляции и отопления зданий рассчитывают по законам аэродинамики. При этом используют уравнение Бернулли для газа (см. с. 48), в котором фигурируют давления, а не напоры. Даже водяное отопление рассчитывают именно по давлениям, так как в нём имеет место изменение температуры жидкости и, соответственно, её плотности, поэтому применять величины напоров неудобно. Аэродинамический расчёт этих сетей сводится к определению действующей разности давлений D p_пр (вызывающей в них движение), потерь давления в них D p_пот, скоростей, расходов и геометрических размеров проходных сечений.

Расчёт ведётся по уравнению Бернулли так. Надо подобрать такие размеры трубопроводов, каналов и их проходных сечений (которые создают сопротивления потоку), чтобы скорости потоков были допустимыми, расходы удовлетворяли нормам и разность давлений D p_пр была равна потерям давления в сети D p_пот, причём для запаса надёжности потери искусственно увеличивают на 10 %. Поэтому для расчёта инженерных сетей уравнение Бернулли применяют в такой записи:

D p_пр = 1,1 D p_пот, (68)

и сеть окончательно должна удовлетворять этому равенству.

Вычисление разности давлений D p_пр будет рассмотрено ниже на примерах расчётов топки с дымовой трубой и водяного отопления с естественной циркуляцией.

Потери давления D p_пот в трубопроводе, воздуховоде или газопроводе можно найти по формуле Вéйсбаха для газа:

(69)

где z — коэффициент гидравлического сопротивления, тот же, что и для жидкости (см. с. 26), только в случае некруглого сечения надо использовать величину эквивалентного диаметра d_э вместо d.

Общие потери давления D p_пот складываются из суммы линейных D p_l и местных D p_м потерь:

(70)

Для вычисления D p_l и D p_м применяется формула Вéйсбаха для газа (69), в которой вместо z подставляют соответственно z_l или z_м (см. с. 26-28), а вместо d — d_э.

Например, при определении D p_l коэффициент линейного гидравлического сопротивления (величина безразмерная)

z_l = l l / d_э, (71)

где l — длина прямолинейного участка сети.

Коэффициент гидравлического трения l при турбулентном режиме (практически всегда в газовых потоках) определяется по формуле (32) с. 27 в виде

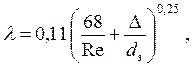(72)

где D — шероховатость стенок трубопровода или канала, мм. Например, вентиляционные короба из листовой стали имеют D = 0,1 мм, а воздуховоды в кирпичной стене D = 4 мм.

Значения коэффициента местных гидравлических сопротивлений z_м принимают по справочным данным для конкретных участков деформации потока (вход и выход из трубы, поворот, тройник и т.д.).

 

Расчёт систем с естественной тягой

 

Работа печных труб и вентиляционных систем зданий, удаляющих дым и несвежий воздух из помещений, основана на естественной тяге D p_е — разности приведённых полных давлений внутри и снаружи, Па.

Естественная тяга D p_е (Па) находится по формуле

D p_е = g h (r_н – r_в), (73)

где h — высота печной (дымовой) трубы или вентиляционной шахты; r_н — плотность наружного (холодного) воздуха; r_в — плотность внутреннего (тёплого) воздуха по формуле (55).

Рассмотрим пример расчёта топки (рис. 29). При горении топлива в топке тяга дымовой трубы способствует удалению горячих газов. Тяга возникает из-за разности температур: горячего воздуха внутри топки t_в ° и холодного — снаружи t_н °. Разные температуры соответствуют разным плотностям воздуха r_в и r_н. Из-за малых скоростей V в таких системах динамическое давление p_д = r V ²/2 не учитывается. Тогда, подставляя в уравнение Бернулли для газа (65) приведённые полные давления для точек А и В (см. рис. 29), придём к формуле естественной тяги (73) и определим D p_е.

 

Следующим шагом расчёта является нахождение общих потерь давления D p_пот (см. с. 50) и сравнение их с величиной тяги D p_е. Если достигнуто равенство (68), то расчёт закончен, система будет работать нормально — удалять дым. Если равенство (68) не соблюдается, то нужно конструктивными мероприятиями изменить или тягу, или потери. Например, тягу можно увеличить двумя способами:

— сделать выше трубу;

— увеличить разницу температур (что не всегда возможно).

Потери давления будут меньше, если будет:

— больше проходное сечение трубы;

— короче путь прохождения удаляемых газов;

— меньше поворотов и других местных сопротивлений;

— меньше шероховатость стенок каналов.

Системы естественной вентиляции в зданиях по удалению несвежего воздуха из помещений работают и рассчитываются точно по таким же принципам.

 

Расчёт систем с естественной циркуляцией

 

На рис. 30 схематично изображена система водяного отопления — это типичная система с естественной циркуляцией. Стрелками показан круговорот воды. За счёт чего же она «крутится»?

 

При нагревании воды в водогрейном котле она становится горячей и приобретает плотность r_г, отличную от плотности холодной воды r_х. Для расчёта таких систем упрощённо принимают, что температура и плотность резко изменяются только в центре нагревания (котле) и центре охлаждения (отопительном приборе — радиаторе). Возникает естественное давление D p_е — так принято называть разность приведённых полных давлений в котле и радиаторе, Па. Оно и приводит в движение воду в таких системах, гоняя её по замкнутому кругу, — это называется естественной циркуляцией.

Формула для естественного давления D p_е выводится, как и в предыдущем примере, с помощью уравнения Бернулли для газа:

D p_е = g h (r_х – r_г), (74)

где h — расстояние по высоте между центром нагревания и охлаждения (см. рис. 30).

После вычисления D p_е рассчитывают общие потери давления D p_пот при движении воды по трубопроводам циркуляционного кольца от точки В к А (см. рис. 30) с использованием формулы (69).

Если соблюдается равенство (68) — расчёт закончен, система будет работать нормально — обогревать помещение. Если равенство не соблюдается, то надо корректировать или естественное давление D p_е, или потери D p_пот. Как этого добиться — подумайте сами (см. с. 52).

Архитектурно-строительная аэродинамика

 

При возведении зданий строители сталкиваются с воздействием ветра — с так называемыми ветровыми нагрузками. Потоки воздуха обтекают здания, сооружения, строительные механизмы (краны и т.д.) и стремятся опрокинуть их. При ветре на поверхности домов возникают зоны повышенного и пониженного давления, что может привести к продавливанию ограждающей конструкции или к её отрыву. При сильных ветрах срывает крышу или её отдельные элементы. Перепад давлений с разных сторон дома приводит к сквознякам в помещениях через окна, балконные двери и даже через стены. Рассмотрим аэродинамическую суть этих явлений.

При обтекании здания воздушным потоком линии тока огибают его коробку, причём за зданием в подветренной зоне образуется вихрь и область пониженного давления (рис. 31). В передней же наветренной части давление воздуха, наоборот, повышается.

Ветровое давление вычисляется по формуле

(75)

где k_в — коэффициент изменения ветрового давления по высоте; C_аэр — аэродинамический коэффициент (безразмерный); p_д = r V ² / 2 — — динамическое давление, Па; r» 1,22 кг/м ³ — плотность воздуха, обычно принимаемая в строительных расчётах; V — скорость ветра, м/с.

 

 

Коэффициент k_в с увеличением высоты от поверхности земли возрастает обычно с 0,4 до 1,5 (ветер с высотой усиливается). В первом приближении его можно принимать k_в» 1.

Аэродинамический коэффициент C_аэр в общем случае является функцией формы обтекаемого тела и числа Рéйнольдса. Он характеризует условия обтекания здания в зависимости от его конфигурации в плане и разрезе и ориентации по отношению к господствующему направлению ветров. В строительных расчётах его принимают в виде констант.

Аэродинамический коэффициент C_аэр имеет численные значения между 1 и 0 (по абсолютной величине). Например, для наветренной (фронтальной) стены дома C_аэр = +0,8, а с противоположной (подветренной) стороны коэффициент C_аэр = –0,6 (рис. 32). Знак «минус» указывает, что давление ветра направлено от стены, ветер стремится оторвать конструкцию от здания. Знак «плюс» — давление направлено к стене.

Для выяснения картины распределения ветрового давления p_ветр по поверхности здания строят эпюры давления (см. рис. 32). Их ординаты вычисляют по формуле ветрового давления (75). Значения динамического давления p_д принимают в готовом виде по нормативной литературе для рассматриваемого географического района строительства или же вычисляют по скорости ветра V из наблюдений метеорологов, если район малоизучен. Реальные эпюры ветрового давления p_ветр имеют криволинейное очертание, однако в строительных расчётах применяют упрощённо прямоугольные эпюры (см. рис. 32).

 

 

 

 

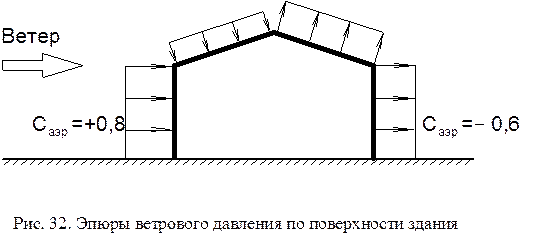
Фильтрация газа

 

Фильтрация газа, то есть его движение через пористые среды, в области строительства имеет особое значение для ограждающих конструкций зданий: стен, покрытий.

Зимой холодный воздух проникает в помещения через поры и микротрещины стен, через щели окон, балконных дверей — происходит так называемая инфильтрация воздуха, порождающая сквозняки и понижение температуры. Поэтому проницаемость ограждающих конструкций зданий ограничивается строительными нормами.

Для расчёта скорости фильтрации газа используется закон Дарсú в виде:

(76)

где k ₀ — проницаемость пористой среды, м ²; m — динамическая вязкость газа, Па·с; D p_пр — разность приведённых полных давлений, вызывающая движение газа, Па; l — длина пути фильтрации, м.

Закон Дарсú в этой записи для газа применяется во всех областях техники, например, при расчёте притока природного газа к буровым скважинам на газовых месторождениях. Он позволяет рассчитывать фильтрацию газа только в ламинарном режиме.

Однако в строительстве для расчётов фильтрации воздуха через ограждающие конструкции зданий этот закон применяют в другом виде (для ламинарного и турбулентного режима движения газа)

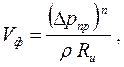(77)

где r — плотность воздуха, кг/м ³; R_u — сопротивление воздухопроницаемости строительного материала, м ²· ч · Па/кг (принимается по строительным нормам для соответствующей толщины материала d); n = 1 — для стен и покрытий (ламинарный режим фильтрации); n = = 2 / 3 — для окон и балконных дверей (турбулентный режим).

Следует помнить, что перед расчётом по формуле (77) все исходные величины надо перевести в единицы СИ!

Таким образом, закон Дарсú (76) и (77) позволяет вычислять объёмный расход газа (воздуха) Q = V_ф w, проходящего через конструкцию толщиной l (или d) с площадью поперечного сечения w. Для пересчёта Q в весовой расход его умножают на удельный вес газа g.

⇐ Предыдущая12345Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: