Потери в скачках уплотнения

Рассмотрим более подробно энергетические преобразо­вания в скачках. Предполагая энергетически изолированное течение, заключаем, что полная энергия потока при пере­ходе через скачок не меняется. Это значит, что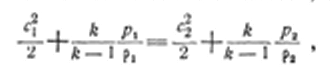

или, пользуясь параметрами полного торможения,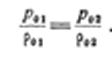

Условие можно заменить эквивалентным условием постоянства энтальпии торможения при переходе через скачок:

или при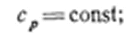

Имея в виду эти условия, рассмотрим процесс скачка в диаграмме is. Зная давление торможения до скачка p_tl и энтальпию торможения /_#, найдем в диаграм­ме is точку О,, характеризующую состояние иэоэнтропи- чески заторможенного газа до скачка. По известной ско­рости потока до скачка с, или давлению р_х находим точку D, которая определяет состояние движущегося газа перед скачком. В скачке статическое давление потока уве­личивается до р,. Если известен угол отклонения потока I и, следовательно, (3, то состояние газа за скачком опреде­лено, так как по формуле можно найти приращение энтропии &s*. Заметим, что ли­ния, соединяющая точки D и F._t на рис. 4-11, не характе­ризует изменения состояния газа в скачке, так как в диаграмме из неквазистатнческие процессы могут быть представ­лены тольео начальной и конечной точками процесса.

Если поток за скачком кэоэнтропически затормозить, то состояние латного торможения характеризуется точкой 0„ в которой легко находится значение. Если предоставить теперь потоку возможность нзоэнтролически расшириться до давления перед скачком, то его состояние будет опре­делено точкой Е. Скорость газа при этом может быть вычислена по уравнению энергии:

25. Постр-ие проц-са в диагр-е i-s диагр-е. Скачки уплотн-я в реал-ом газе

рассмотрим процесс скачка в диаграмме is. Зная давление торможения до скачка р01 и энтальпию торможения, найдем в диаграмме is точку характеризующую состояние изоэнтропически заторможенного газа до скачка. По известной скорости потока до скачка г или давлению, находим точку, которая определяет состояние движущегося газа перед скачком. В скачке статическое давление потока увеличивается. Если известен угол отклонения потока и давление, то состояние газа за скачком определенно.

Если поток за скачком изоэнтропически затормозить, то сост-е полного торможения харак-ся точкой, в кот-й легко находится значение p. Если предоставить теперь потоку возм-сть изоэнтропически расшириться до давления перед скачком, то его состояние будет определено точкой Е2. Скорость газа при этом может быть вычислена по урав. энергии: 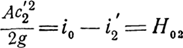(ккал/кг)

где H02 — изоэнтропический перепад энтальпий за скачком. Величину H02 можно рассматривать как сумму Hо2=Н0к + Hon

где Н0к — кинетическая энергия потока за скачком:

Н0п — изменение потенциальной энергии потока в скачке.

При обтекании тела сверхзвуковым потоком перед телом возникает ударная волна (скачок уплотнения); при переходе через эту волну энтропия газа растет, а скорость уменьшается.

Таким образом, в сверхзвуковом потоке идеальной жидкости появляется особый вид сопротивления — волновое сопротивление, зависящее от потерь в скачках, а следовательно, от формы и интенсивности скачков. Как мы видели, форма скачка и его интенсивность зависят от формы тела и скорости обтекания. Учитывая, что при уменьшении угла отклонения потери в скачке уменьшаются, можно заключить, что остроконечные тела в сверхзвуковом потоке должны обладать меньшим сопротивлением, чем тела, имеющие скругленную форму.

Изменение потерь в скачках в завис-ти от их инт-сти можно проследить в тепловой диаграмме построение „ударной поляры*.

Для расчета скачков оказывается весьма удобным пользоваться специальными диаграммами. Такие диаграммы позволяют легко определить характеристики скачка по двум заданным параметрам.

Пересечение скачков

Cлучай пересечения двух косых скачков показан на рис.1. Косые скачки возникают в результате поворота двух противоположных стенок канала на разные углы ơ1 и ơ2. Направления потока в зонах II и III будут неодинаковыми, в зоне III отклонение будет больше на угол ơ ₂ — ơ ₁. Параметры течения за косыми скачками АВ и А₁В легко могут быть определены по известным параметрам до скачков ƛ₁ р₁, T₁ и углам ơ1 и ơ2, если эти углы меньше соответствующего максимального значения ơ_m для данного вектора скорости ƛ₁.

Параметры потока в области IV можно найти, исходя из граничных условий для линии тока, проходящей через точку В. Примем, что направления скоростей и давления во всех точках области IV будут одинаковыми. Отсюда определяется угол между вектором скорости в зоне IV и вектором ƛ₁. Действительно, если результативное отклонение потока в зоне IV обозначить ơ ₄ то из рассмотрения легко установить, что отклонение потока при пересечении скачка BC1 равно ơ1 + ơ2, а при пересечении ВС оно равно ơ2 – ơ4. Задаваясь различными значениями давления в зоне IV (p4) или по диаграммам косых скачков, находим углы наклона скачков ВС и BC1 и углы отклонения потока ơ1 + ơ4 и ơ2 - ơ4. Значение р4, при котором величины ơ4 определенные по параметрам зон II и III, будут одинаковыми,

можно найти, построив зависимости ơ ABC1 и ơABC от р4. Точка пересечения этих кривых даст искомое значение ơ4. Зная величину ơ4, находим углы косых скачков βBC1 и βBC.

Изменение состояния газа вдоль двух линий тока, пересекающих зоны // и III, в тепловой диаграмме показано. Суммарное приращение энтропии для этих линий тока будет одинаковым только в тех случаях, когда ơ1 = ơ2. Если интенсивность скачков АВ и А1В различна, то приращение энтропии вдоль рассматриваемых линий тока будет различным (точки 4 и 4' на рис. 1,б).

При этом, если во всех точках зоны IV давления одинаковы, скорости, температуры и плотности за скачками ВС 1 и ВС будут различными. Вдоль линии тока, проходящей через точку В, образуется тангенциальный разрыв скоростей, в результате чего в вязком газе возникает вихрь.

Устойчивое существование системы двух пересекающих косых скачков возможно не при всех условиях. Если углы вторых скачков βBC и βBC1 будут больше соответствующих значений βm, характер течения меняется. Вблизи нейтральной линии тока, проходящей через точку В, образуется криволин-й скачок. С-ма пересек-хся прямолин-х косых скачков переходит в мостообразный скачок. Потери энергии в потоке при этом увелич-ся.

27. Ступенчатое торможение Потока

Ступенчатое торможение потока можно получить, применяя различные системы косых скачков. Если при заданных пределах изменений статического давления увеличивать число косых скачков путем увеличения последовательных поворотов стенки, то торможение потока будет более плавным, а суммарные относительные потери будут уменьшаться.

Обычно за последним косым скачком располагают прямой скачок, на котором происходит переход к дозвуковой скорости.

Коэффициент суммарных потерь в системе двух скачков, очевидно, будет равен:

При больших сверхзвуковых скоростях для перехода к дозвуковым скоростям целесообразно применять более сложные системы скачков, состоящие из нескольких косых и одного завершающего прямого скачка. С ростом числа косых скачков потери энергии будут уменьшаться. Для каждой скорости потока v₁ при заданном числе косых скачков существует оптимальная схема расположения скачков, которую можно найти последовательным расчетом.

 

Отражение скачков

Отражение от твердой стенки

Расчет отраженного скачка не встречает затруднений. Зная параметры [_невозмущенного течения А,, р_г и угол отклонения 8, с помощью диаграммы скачков легко определяем параметры потока за первичным скачком: Я₂, р_г и (З_а. При том же значении 8 находим состояние газа за отраженным скачком: Я_а, p_s и (5₃. Изложенным выше способом находим потери энергии в первичном и отраженном скачках. Следует иметь в виду, что такое отражение косого скачка возможно не всегда. Если "уго'л отклонения 8 больше максимального значения для скорости А₂, то картина отражения меняется. Допустим, что в диаграмме ударных поляр (рис. 4-25,а) отрезок OD изображает скорость потока до скачка А,. Если угол отклонения стенки 8<8_ш2, то гипоциссоида, отвечающая скорости за скачком Я_а (отрезок 02), пересекает линию вектора (точки 3 и 4).

б) Отражение от свободной границы струи

Такое отражение рассмотрено на рис. 4-26. Во всех точках на границе FBE давление одинаково и равно давлению внешней среды р_а. В струе это же давление имеет место только до скачка АВ. При переходе через скачок АВ давление изменяется от р_х = р_а до p_t > р_а. Следовательно, точке В свойственны одновременно два давления: р_а со стороны среды и р_г со стороны струи. Такая точка является очагом возмущения сверхзвукового течения, создающим стационарную волну разрежения. При обтекании точки В давление потока должно упасть от р₂ до р_а, что и приводит при сверхзвуковых скоростях к образованию волны BCD.

 

29. Взаимодействие скачка и волны разрежения

При обтекании тел конечных размеров сверхзвуковым потоком совершенного газа интенсивность скачков на раз­личных расстояниях от тела будет различной. Благодаря взаимодействию с волнами разрежения по мере удаления от тела интенсивность скачков уменьшается и на бесконеч­ном удалении становится бесконечно малой.

Рассмотрим в качестве примера обтекание заостренной пластинки (рис. 4-27). На переднем остром (5<8_т) носике пластинки возникает плоский косой скачок АВ. При об­текании точки D образуется стационарная волна разреже­ния, причем характеристика, на которой начинается от­клонение потока, расположена под углом

a_m2 = arcsin^,

где М₂ — скорость за скачком.

волной разрежения М₃ определяется по отношению — Ро 2

где р₀₂ — давление торможения за косым скачком.

Отражение скачка приводит к деформации границы струи, которая в точке В отклоняется на угол 8₂>V9to отклонение вызывается расширением струи. Таким образом, при отражении от свободной границы струи, вдоль, которой давление сохраняется постоянным или падает, скачок уплот­нения преобразуется в волну разрежения. Если давление вдоль границы возрастает, то в зависимости от интенсив­ности изменения давления отражение может быть погашено или оно происходит с сохранением знака (как и от твер­дой стенки)

30. Конические скачки уплотнения

В предыдущих параграфах настоящей главы были рас­смотрены скачки уплотнения в плоском течении. При об­текании осесимметричных тел поверхности разрыва имеют осесимметричную форму. Рассмотрим особенности осесим­метричного скачка на примере обтекания кругового конуса. Перед конусом образуется конический скачок, вершина которого совпадает с вершиной конуса, если угол раствора конуса меньше максимального значения для данной скорости набегающего потока.

Основные соотношения при переходе через поверхность конического скачка, как легко видеть, будут теми же, что и для плоского скачка. При одинаковых углах раствора клина и конуса скачок на конусе будет иметь меньший угол наклона, чем на клине, так как конус вызывает меньшие стеснения потока, чем клин бесконечного размаха того же угла раствора. При переходе через конический скачок линии тока, так же как и в случае плоского скачка, претерпевают излом. Однако так как скачок на конусе слабее, чем на клине, непосредственно за скачком линии тока будут наклонены к вектору скорости невозмущенного потока под углом, меньшим угла раствора конуса у₀. Расчеты показывают, что в возмущенной области линии тока не являются прямыми как при обтекании клина, а кривыми, причем кри­визна их различна и зависит от расстояния от поверхности конуса. Кривизна линий тока, ближайших к поверхности конуса, весьма мала.

31. Скачки конденсации (тепловые скачки)

Основная идея теории В. А. Андреева и С. 3. Беленького — исследование прямых и косых скачков конденсации как тепловых скачков. Эта теория развита ими применительно к воздуху с небольшим содержанием водяных паров. Изменение массы газа в процессе конденсации считается пренебрежимо малым. Та же теория была применена М. Е. Дейчем [15] для влажного пара. В обоих случаях считается, что при прохож-и через скачок полная энтальпия меняется. В урав-и энергии вместо плотности паровой фазы вводится плотность влажного пара. В результате этих допущений были получены простые зависимости между параметрами пара перед скачком и за ним.

Следует особо подчеркнуть, что сейчас анализируются свойства только теплового скачка, а не процессов горения или конденсации в целом. Для анализа задачи в целом необходимы дополнительные сведения о процессе.

Рассмотрим скачок конденсации в предположении 1) пар перед скачком переохлажден и не содержит капелек жидкости 2) насыщенный пар и мелкие капельки жидкости за скачком находятся в тепловом равновесии 3) скорости капелек жидкости за скачком равны скорости пара.

Общее между тепловым скачком и скачком конденсации состоит Б том, что в обоих случаях к потоку подводится теплота. Однако в тепловом скачке эта теплота подводится извне, и поэтому энтальпия торможения после скачка возрастает. В скачке конденсации теплота выделяется при конденсации части текущего пара и поэтому полная энергия потока до и после скачка остается постоянной. Кроме того, различие состоит в том, что после скачка давление и температура связаны условием фазового равновесия. Поэтому количество выделившейся при конденсации теплоты не может быть установлено произвольно, а связано с интенсивностью скачка.

Следует различать конденсационные скачки в одно-, двух- и многокомпонентных средах. В последнем случае в потоке неконденсирующегося газа (или смеси газов) присутствуют пары конденсирующейся среды. Например, пары воды в сверхзвуковом потоке воздуха при определенных условиях спонтанно конденсируются к потоку воздуха подводится скрытая теплота парообразования и его полная энергия (энтальпия торможения) возрастает. Такие скачки иногда называют тепловым и Ч Скачки конденсации в однокомпонентной среде не выз-ют изменения энтальпии торможения.

32. Температура торможения в вязкой жидкости

При рассмотрении движения реальной (вязкой) жидко­сти необходимо учитывать диссипацию (рассеяние) энер­гии, вызываемую внутренним трением и теплопроводностью, т. е. термодинамической необратимостью процесса.

Движение вязкой жидкости описывается системой урав­нений сохранения: расхода, количества движения и энергии. Уравнение неразрывности , как уже указывалось, справедливо и для вязкой жидкости. Уравнения количе­ства движения в форме Эйлера должны быть до­полнены членами, учитывающими влияние вязкости.

При рассмотрении движения вязкой жидкости с нерав­номерным распределением скоростей в потоке условие эквивалентности теплоты трения и работы трения не вы­полняется. В таком потоке только часть работы трения превращается в теплоту, а другая часть вызывает чисто механический эффект: перестройку поля скоростей, в про­цессе которой происходит перераспределение кинетической энергии между частицами жидкости. Отсюда вытекает, что различные частицы приобретают разное количество теплоты трения и имеют разный запас полной энергии.

Следовательно, условие i₀ = const в общем случае не яв­ляется интегралом уравнения энергии для всей массы жидкости, так как в потоке образуется местное перерас­пределение энергии.

33. Условия газодинамического подобия

34. Одномерное теч-е газа при нал. трения. Осн. Урав-я

Основными уравнениями установившегося адиабатиче­ского движения вязкого газа являются уже известные нам уравнения неразрывности, количества движения и энергии.

Уравнение импульсов одномерного установившегося по­тока без энергетического обмена с внешней средой при наличии трения можно записать в таком виде:

cdc+^df + dX_T р = 0,

где dX _tp— единичный импульс сил трения.

из­менение параметров течения в трубке переменного сечения происходит под воздействием двух факторов: деформации потока (изменение сечения трубки) и сил трения. Уравне­ния показывают, что влияние трения всегда является одно­сторонним. Так, например, при дозвуковых скоростях (А< 1) в суживающейся трубке (dF < 0) трение способствует ускорению течения (dl^> 0 и dp<^ 0). При сверхзвуковых скоростях в такой же трубке (dF < 0) трение приводит к замедленному падению скорости и соответственно к более медленному возрастанию давления по сравнению с идеаль­ным процессом без потерь.

Сопоставляя влияние изменения сечения трубки (дефор­мации трубки тока) и влияние трения, можно заключить, что в дозвуковом и сверхзвуковом потоках трение приво­дит с качественной стороны к такому же изменению ско­рости течения, как и уменьшение сечения трубки.

Следовательно, воздействие сил трения в потоке можно заменить эквивалентной деформацией струи — уменьшением ее сечения в направлении движения.

Правомочность такой замены вытекает из следующих рассужде­ний. Движение газа в трубе без энергетического обмена, но при на­личии сил трения является необратимым адиабатическим процессом. Такой процесс, как нам уже известно, сопровождается ростом энтро­пии

35. Движение газа в цилиндрической трубе

Критическая скорость течения может возникнуть только в выходном сечении цилиндрической трубы. Действительно, согласно уравнению при λ<1 и dλ> 0 поток в трубе ускоряется, а при λ>1 и dλ <0 он замедляется. Случай λ = 1 в промежуточном сечении трубы противоречит уравнению и физически нереален.

Макс-ое значение приведенной длины трубы вы­р-ся формулой

 

 

Кривые иллюстрируют невозможность пере­хода в цилиндрической трубе из одной области скоростей в другую. В такой трубе, как было показано выше, при определенной скорости на входе λ ₁ и соответствующей длине на выходе достигается критическая скорость.

Таким образом, уравнение показывает, что для цилиндрической трубы заданных размеров L и D при скорости на вы­ходе из трубы λ ₂ = 1 и для определенных значений k и С безразмерная скорость на входе в трубу λ _х, а вместе с тем и приведенный расход газа q₁ имеют строго опре­деленные значения.

При дозвуковой скорости на входе в цилиндр-ую трубу длиной L, харак-ую коэф-том сопротив­ления С, при установ-ся движении может пройти мак-ное количество газа, если λ ₂ = 1.

Абсолютный расход газа через трубу предельной длины будет =:

Т. образом, для увел-ия абсол-го расхода газа через цилиндр-ую трубу опред-ных размеров необходимо увел-ть давление полного торможения на входе в трубу или — при постоянном значении р₀ — умень­шать t торможения Т₀. При этом в выходном сечении трубы будет по-прежнему критическая скорость, абсолютное значение которой уменьшается по мере сниже­ния t торможения. Однако расход будет уве­л-ся за счет увел-ния плотности

⇐ Предыдущая123456Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: