 |
Общие методические указания
|
|
|
|
Контрольная работа выполняется в отдельной тетради, страницы которой должны иметь нумерацию и поля. Задачи решаются в том порядке, в каком они приведены в задании.
Перед решением задачи записываются ее условия и исходные данные для требуемого варианта. Решения задач должны быть снабжены краткими пояснениями. В случае необходимости нужно делать ссылки на литературу. Чертежи и схемы должны быть выполнены аккуратно, с помощью линейки и циркуля. В конце работы приводится список использованной литературы, подпись студента, дата окончания.
Работа, выполненная небрежно, отсылается студенту для переоформления. Работа, выполненная не полностью или не по требуемому варианту, не зачитывается.
Работа высылается в институт для рецензирования. После получения прорецензированной работы студент должен исправить отмеченные рецензентом ошибки и выполнить его указания. Если работа не зачтена, то ее необходимо переделать в той же тетради в соответствии с замечаниями рецензента. Работа над ошибками приводится после текста основного задания, после чего работа вновь высылается на проверку. Без предъявления зачтенной контрольной работы студент не допускается к сдаче экзамена по курсу.
Приведенные задачи охватывают основной теоретический материал курса ЦСК и СЭ ч. 2.
К задачам 1, 2.
[2, с. 74-80; 1, с. 275-278]
Для того чтобы произвести расчет числа каналов в обходном направлении, необходимо вначале определить параметры избыточной нагрузки: математическое ожидание (интенсивность) нагрузки при расчетах по п. а) и математическое ожидание и дисперсию, если расчет проводится по п. б).
Проводим расчет по п. а). При этом рассматривается каждый пучок каналов в прямом направлении Vi, i =1,2,...,5, на который поступает пуассоновский поток нагрузки. Считаем пучок полнодоступным. Тогда расчет матожидания избыточной нагрузки ведем по формуле
|
|
|
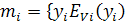 , (1)
, (1)
где  -вероятность отказов в полнодоступном пучке при поступлении пуассоновского потока и экспоненциальном законе распределения времени обслуживания (первая формула Эрланга).
-вероятность отказов в полнодоступном пучке при поступлении пуассоновского потока и экспоненциальном законе распределения времени обслуживания (первая формула Эрланга).
Для i - го пучка каналов имеем
 =
=  (2)
(2)
где  - интенсивность поступающей на пучок нагрузки;
- интенсивность поступающей на пучок нагрузки;
Vi - число каналов в пучке.
По формуле (2), пользуясь программой для МК, провести расчеты избыточных нагрузок от всех пяти первичных пучков каналов.
Для случая а) считаем, что избыточные потоки от пяти первичных пучков являются пуассоновскими.
Определяем интенсивность потока на обходное направление:
M= 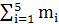 (3)
(3)
Теперь получаем схему для расчета обходного направления. Обходное направление - это полнодоступный пучок, на который поступает пуассоновский поток интенсивностью М (рис. 3). Зная норматив вероятности отказов на обходном направлении (1%), методом подбора, пользуясь формулой (2) или данными [16], [15, с.28-33], можно найти величину Vобх.
Однако избыточные потоки, как показывают измерения на реальных сетях, не являются пуассоновскими, для которых характерен равномерный характер поступления вызовов и дисперсия нагрузки равна математическому ожиданию 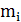 =
= 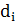 . Для избыточного потока характерно неравенство
. Для избыточного потока характерно неравенство 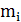 <
< 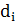 , т.е. он характеризуется наличием малых отрезков времени, на которых имеются большие скопления вызовов, и больших отрезков времени, когда вызовы отсутствуют. Поэтому расчеты Vобх по формуле (2) будут неточными, а это приведет к тому, что сеть не будет обеспечивать заданную норму потерь.
, т.е. он характеризуется наличием малых отрезков времени, на которых имеются большие скопления вызовов, и больших отрезков времени, когда вызовы отсутствуют. Поэтому расчеты Vобх по формуле (2) будут неточными, а это приведет к тому, что сеть не будет обеспечивать заданную норму потерь.
Робх=0,01
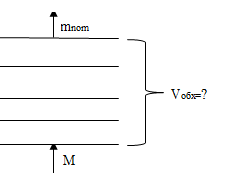
Рис. 3.
По этой причине расчет лучше вести методом эквивалентной замены, предложенным Вилкинсоном. Для каждого избыточного потока вычисляется математическое ожидание нагрузки mi по формуле (1), что сделано в расчетах п. а) задания. Помимо этого, нужно определить величины дисперсии избыточных нагрузок от всех прямых пучков:
|
|
|
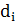 =
= 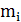 (1-
(1- 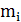 +
+ 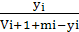 ) (4)
) (4)
Для объединенного избыточного потока, поступающего на обходное направление, имеем:
M= 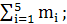 D=
D= 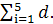 (5)
(5)

Рис. 4.
Для учета колеблемости поступающего потока при расчете числа каналов в обходном направлении Vобх следует использовать метод "эквивалентной замены" Вилкинсона. Производим эквивалентную замену пяти первичных полнодоступных пучков (см. рис. 1), на каждый из которых поступает нагрузка интенсивностью yi -, одним полнодоступным пучком емкостью S (рис.4). Рассматриваем всю эту схему как один полнодоступный пучок емкостью Vобх + S, на вход которого поступает эквивалентная нагрузка yэ. Значения yэ и S можно определить методом подбора по формулам (1) и (4), если у заменить на yэ,а  на
на  , т.е. рассматриваем нижнюю часть схемы рис. 4 как полнодоступный пучок в S каналов, на который поступает пуассоновский поток интенсивностью yэ, что создает избыточную нагрузку с интенсивностью М и дисперсией D.
, т.е. рассматриваем нижнюю часть схемы рис. 4 как полнодоступный пучок в S каналов, на который поступает пуассоновский поток интенсивностью yэ, что создает избыточную нагрузку с интенсивностью М и дисперсией D.
Однако проводить расчеты по этим формулам очень сложно и лучше пользоваться простыми, хотя и приближенными формулами:
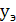 = D + 3
= D + 3  (
( – 1); (6)
– 1); (6)
S = 
 – M – 1. (7)
– M – 1. (7)
Число каналов S может быть дробным. Далее рассматриваем пучок (Vобх + S) каналов (рис. 4). Из (6) и (7) найдены S и 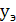
Потери в эквивалентной схеме рис. 4 можно рассчитать по формуле:
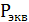 =
=  ,
,
где Ps - потери в пучке в S каналов, которые можно найти как отношение интенсивности потерянной и пропущенной нагрузки:
 =
= 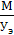
Нормативное значение потерь в обходном направлении Робх. н, известно и равно 0,01.
Отсюда можно определить Рэкв по формуле:
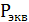 =
= 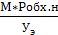 . (8)
. (8)
Рассматривая (S + Vобх) как общий полнодоступный пучок, можно применить для его расчета формулу Эрланга:
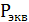 =
=  * (
* ( ). (9)
). (9)
Из (9) методом подбора или используя [161, [14, с- 28-33], можно найти величину (Vобх + S). Зная число каналов в эквивалентном пучке, нетрудно найти Vобх.
К задачам 3, 4
Материал к задачам 3 и 4, посвященный изучению метода рельефов динамического управления потоками вызовов, изложен в основной литературе [2, с.121-126] и дополнительной [6, с. 172-174; 9; 4, с. 56-59]. Схемы децентрализованной и централизованной систем управления потоками можно найти в [4, с. 35-39].
|
|
|
По заданию требуется построить рельеф только для одного i -го УК. Построенным i -рельефом можно пользоваться только при установлении соединения от любого другого УК j к узлу i.
Фиксируется соседний с УКi. узел j. Стрелка, исходящая от узла j к узлу i и показывающая вес этого направления, должна иметь высоту 1, что имеет тот физический смысл, что при установлении соединения от УКj до УКi используется путь в один транзитный участок. Если рассмотреть расстояние от узлов, соседних узлу j, то, очевидно, путь установления соединения от этих узлов по направлению к узлу j будет иметь длину на один транзитный блок больше, т.е. 2, и т.д. Присвоение рельефа на графе сети можно проводить, пользуясь следующим простым алгоритмом.
1. Рассмотрим произвольный УКr. Управляющее устройство рассматривает веса исходящих стрелок и выбирает стрелку с минимальной высотой. Эта высота считается высотой узла 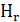 :
: 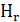 =
= 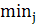 {
{ 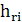 }, где
}, где 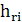 -высота ребра
-высота ребра 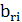 . Физический смысл этого действия заключается в том, что на узле отмечается кратчайший путь в числе транзитных участков.
. Физический смысл этого действия заключается в том, что на узле отмечается кратчайший путь в числе транзитных участков.
2. Высота 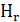 , рассылается соседям. ЭУМ соседнего узла
, рассылается соседям. ЭУМ соседнего узла 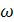 , приняв
, приняв 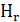 отмечает направление, ведущее от
отмечает направление, ведущее от 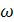 к r, высотой (
к r, высотой ( + 1), придерживаясь того правила, что если путь от соседнего УКr, дo УКi составляет некоторое число транзитных участков, то от УКω этот путь будет на 1 участок длиннее.
+ 1), придерживаясь того правила, что если путь от соседнего УКr, дo УКi составляет некоторое число транзитных участков, то от УКω этот путь будет на 1 участок длиннее.
Придерживаясь такого алгоритма, можно сформировать рельеф всей сети, при этом алгоритм является децентрализованным, каждая ЭУМ работает независимо от ЭУМ других УК. Однако между узлами передается информация об их весах. Пример рельефа для УК показан для графа сети на рис. 4. Для практического использования на сетях связи алгоритм несколько видоизменен. Когда ЭУМ УК ведет просмотр направлений с целью вычисления своей высоты, она учитывает, для какого узла вычисляется высота, и исключает из рассмотрения направление, ведущее к этому узлу. Это позволяет избежать образования петель. Например, если Н3 посылается к УК2,то из рассмотрения исключается высота h32 и в результате Н =3. Новый вес ребра b23 приведен в кружочке. Это позволяет исключить из рассмотрения путь 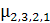 .
.
|
|
|
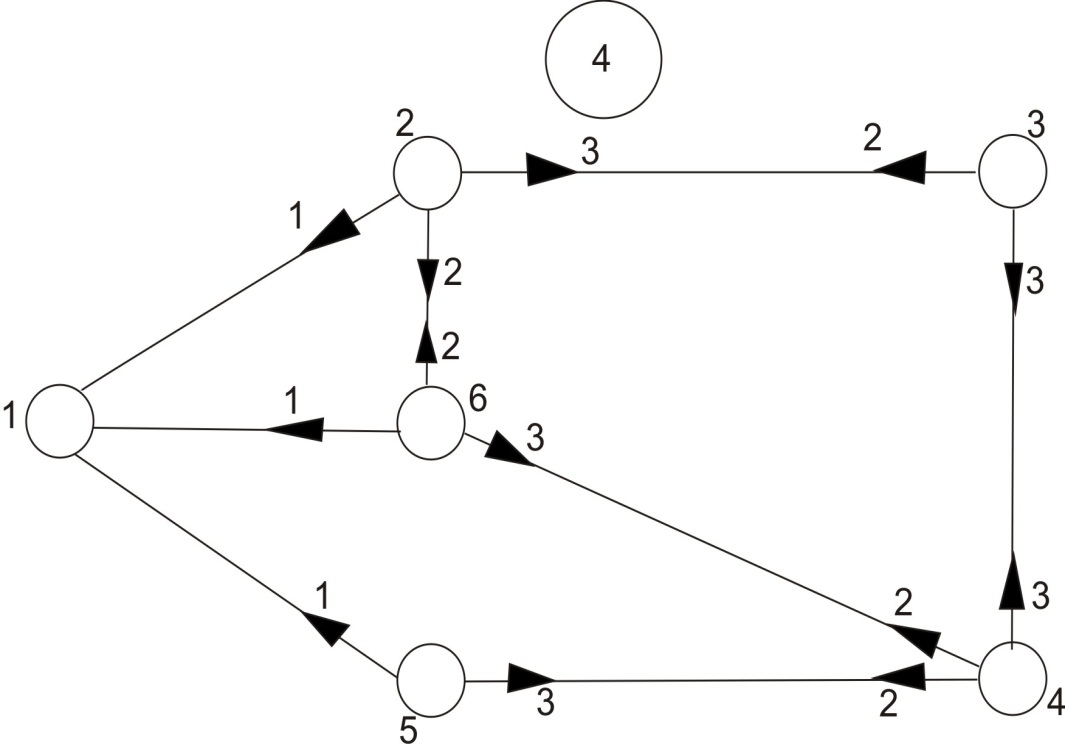
Рис. 5.
Алгоритм метода рельефа обладает свойством исправлять неправильные веса, которые могут возникнуть в том случае, если в сети вышло из строя ребро или им нельзя пользоваться в результате возникшей перегрузки. Управляющее свойство узла, на котором это произошло, сообщает всем своим соседям новый вес, если, конечно, вышло из строя направление с минимальным весом.
Таким образом, рельеф соседних узлов меняется в соответствии с заданным выше алгоритмом. Если высота УК в результате выхода из строя ребра не меняется, изменения рельефа на соседних УК не происходит.
В задании требуется составить матрицу маршрутов для УКj. Лучше всего привести матрицу рельефов и на ней пояснить построение матрицы маршрутов. Пусть матрицу маршрутов требуется построить для УК4 сети, (рис.5). Ниже приведены соответствующие столбцы матрицы рельефа R4 и маршрутов М4. Веса в матрице рельефов обозначают число транзитных участков в кратчайшем пути от УК4 до УК1, если устанавливать соединение по направлению  .
.
Числа в матрице маршрутов задают порядок выбора направлений [4, с. 35-39].
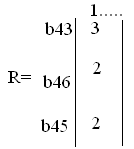
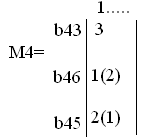
Заметим, что направление 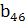 и
и  с точки зрения выбранного критерия равноценны, поэтому в скобках в М4 указан другой возможный вариант порядка выбора.
с точки зрения выбранного критерия равноценны, поэтому в скобках в М4 указан другой возможный вариант порядка выбора.
Если вышло из строя какое-либо ребро сети, то необходимо провести изменение рельефа (лучше всего это сделать на новом чертеже графа сети), затем сформировать для этого случая заданный столбец матриц рельефа и маршрута.
К задаче 5
Материал к задаче 5, посвященной изучению метода распределения потоков нагрузки на ГТС при проектировании новой станции, изложен в литературе [17]. В соответствии с методом Раппа предполагается, что включение на сети новой АТС не окажет влияния на общий исходящий поток нагрузки существующих АТС. Нагрузка на новую станцию создается за счет пропорционального снижения нагрузки с существующих направлений и передачи ее на направление к новой АТС.
Пусть матрица потоков нагрузки до включения новой АТС размерностью n*n имеет вид:
 (10)
(10)
В выражении (10) исходящие и входящие потоки нагрузки на АТС определяются суммированием соответствующих строк и столбцов матрицы, общая нагрузка на сети равна сумме элементов матрицы (10):
M= 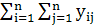
Допустим, что новая (n+1) АТС имеет исходящую нагрузку 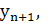 равную входящей, а внутристанционную -
равную входящей, а внутристанционную -  . Для организации столбца (n+1) входящей нагрузки на
. Для организации столбца (n+1) входящей нагрузки на 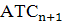 необходимо снять с существующих направлений нагрузку
необходимо снять с существующих направлений нагрузку 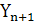 -
-  .
.
Рассчитаем коэффициент снятия нагрузки
X= 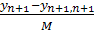 (11)
(11)
который показывает, какую часть нагрузки необходимо снять с каждого Эрланга существующих направлений и передать на новую АТС. Тогда столбец (n+1) для новой АТС запишется следующим образом:
|
|
|
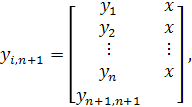 (12)
(12)
а строка для (n+1) АТС:
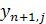 =[
=[ 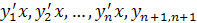 ] (13)
] (13)
Новая матрица распределения нагрузки будет иметь вид:
(14)
Общий поток нагрузки на сети увеличился на величину  , а общие исходящие и входящие потоки нагрузки существующих АТС остались неизменными.
, а общие исходящие и входящие потоки нагрузки существующих АТС остались неизменными.
Методические указания
и контрольные задания
по дисциплине
СЕТИ СВЯЗИ
для студентов заочников 5 курса
(специальность 21070016)
|
|
|


