 |
Дифференциальные уравнения второго порядка
|
|
|
|
Линейные однородные уравнения второго порядка с постоянными коэффициентами
Общий вид такого уравнения: 
где p и q -действительные числа. Корни его характеристического уравнения 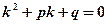 могут быть:
могут быть:
1) действительными и различными: 
2) действительными и равными: 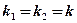
3) комплексными: 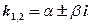
Им соответствуют следующие общие решения уравнения:
1) 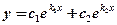 ;
;
2)  ;
;
3)  .
.
Пример 3.
Найти частное решение линейного однородного уравнения второго порядка с постоянными коэффициентами, удовлетворяющее начальным условиям:

Решение:
а) Характеристическое уравнение 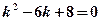 имеет два различных вещественных корня
имеет два различных вещественных корня  , поэтому общее решение этого дифференциального уравнения записывается в виде
, поэтому общее решение этого дифференциального уравнения записывается в виде  , где
, где  произвольные постоянные.
произвольные постоянные.
Отсюда 
Основываясь на начальных условиях, получаем 
Решая систему уравнений  получаем
получаем  =1;
=1; 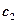 =0.
=0.
Частное решение данного уравнения, удовлетворяющего заданным начальным условиям, приобретает вид 
б) Характеристическое уравнение  имеет два равных корня
имеет два равных корня 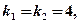 поэтому общее решение соответствующего дифференциального уравнения будет иметь вид
поэтому общее решение соответствующего дифференциального уравнения будет иметь вид  Дифференцируя, получим
Дифференцируя, получим  .
.
Учитывая начальные условия, получаем систему для определения  Откуда
Откуда 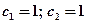 , поэтому частное решение имеет вид:
, поэтому частное решение имеет вид: 
в) Характеристическое уравнение 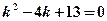 не имеет действительных корней. Его корни:
не имеет действительных корней. Его корни: 
Поэтому общее решение данного уравнения имеет вид: 
Дифференцируя, получим:

Подставляя в выражения для  начальные условия, получим систему уравнений:
начальные условия, получим систему уравнений: 
решая которую, найдем  .
.
Тогда частное решение данного уравнения будет иметь вид: 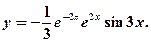
Линейные неоднородные уравнения второго порядка с постоянными коэффициентами
Общий вид такого уравнения: 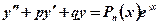 (*)
(*)
В правой части:  многочлен степени
многочлен степени  .
.
|
|
|
Общее решение уравнения (*)может быть представлено в виде

где  - общее решение соответствующего линейного однородного уравнения,
- общее решение соответствующего линейного однородного уравнения,
 - какое- либо частное решение неоднородного уравнения (*).
- какое- либо частное решение неоднородного уравнения (*).
Для отыскания  пользуются следующим правилом:
пользуются следующим правилом:
1) если число  не является корнем характеристического уравнения, то
не является корнем характеристического уравнения, то  где
где  - многочлен степени с неопределенными коэффициентами;
- многочлен степени с неопределенными коэффициентами;
2) если число  совпадает с одним из корней характеристического уравнения, то
совпадает с одним из корней характеристического уравнения, то
 ;
;
3) если число  совпадает с обоими корнями характеристического уравнения, то
совпадает с обоими корнями характеристического уравнения, то
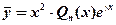 .
.
Пример 4
Найти общее решение линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами: 
Решение:
Будем искать общее решение в виде 
Y – общее решение уравнения 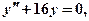 характеристическое уравнение которого
характеристическое уравнение которого  а его корни
а его корни  и решение Y имеет вид:
и решение Y имеет вид:

Частное решение  будем искать в виде
будем искать в виде
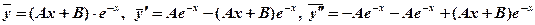 или
или 
Подставим  и
и  в исходное уравнение, получим:
в исходное уравнение, получим:
 или
или

Составим систему для нахождения А и В. 
Тогда частное решение имеет вид:  .
.
Общее решение данного уравнения будет:
 .
.
2 Ряды
Числовым рядом называется выражение
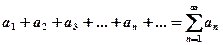 (1)
(1)
Ряд называется сходящимся, если сумма n первых его членов  имеет предел при
имеет предел при 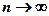 . Иначе ряд называется расходящимся. Ряд может сходиться лишь при условии, когда общий член ряда
. Иначе ряд называется расходящимся. Ряд может сходиться лишь при условии, когда общий член ряда  стремится к нулю при
стремится к нулю при 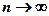 :
:  (Это необходимый, но не достаточный признак сходимости для всякого ряда).
(Это необходимый, но не достаточный признак сходимости для всякого ряда).
Если же  , то ряд расходится. (Это достаточный признак расходимости всякого ряда).
, то ряд расходится. (Это достаточный признак расходимости всякого ряда).
Пример 5. Дан ряд  . Проверить выполнение необходимого признака.
. Проверить выполнение необходимого признака.

Необходимый признак не выполняется. Следовательно, ряд расходится.
Пример 6.
Дан гармонический ряд  . Найдем для него
. Найдем для него  .
.
Для него необходимый признак выполняется, вследствие чего он может быть или сходящимся или расходящимся, что можно установить дополнительным исследованием. (Смотри ниже).
Знакоположительные ряды
Для числовых рядов с положительными членами  , при исследовании сходимости используются следующие достаточные признаки.
, при исследовании сходимости используются следующие достаточные признаки.
|
|
|
Интегральный признак Коши
Ряд с положительными убывающими членами 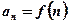 сходится или расходится в зависимости от того, сходится или расходится несобственный интеграл
сходится или расходится в зависимости от того, сходится или расходится несобственный интеграл  , где
, где  - непрерывная убывающая функция.
- непрерывная убывающая функция.
Нижним пределом несобственного интеграла может быть любое число 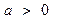 из области определения
из области определения  . Этим признаком можно пользоваться, когда выражение общего члена
. Этим признаком можно пользоваться, когда выражение общего члена 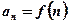 имеет смысл не только для целых положительных значений n но и для всех n, больших некоторого положительного числа т.
имеет смысл не только для целых положительных значений n но и для всех n, больших некоторого положительного числа т.
Пример 7.
Исследовать сходимость гармонического ряда: 

Решение:
Заменяем в выражении общего члена  номер n непрерывной переменно
номер n непрерывной переменно  и убеждаемся, что
и убеждаемся, что 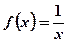 является непрерывной убывающей функции при
является непрерывной убывающей функции при 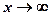 Вычислим несобственный интеграл
Вычислим несобственный интеграл
 .Несобственный интеграл расходится, следовательно, расходится и гармонический ряд.
.Несобственный интеграл расходится, следовательно, расходится и гармонический ряд.
Признак Даламбера
Если  ,то при q <1ряд сходится, а при q >1расходится. При q =1 вопрос о сходимости ряда остается нерешенным.
,то при q <1ряд сходится, а при q >1расходится. При q =1 вопрос о сходимости ряда остается нерешенным.
Пример 8.
Исследовать на сходимость ряд 
Решение:
 .
.
Применим признак Даламбера:
 .Так как
.Так как  то по признаку Даламбера исследуемый ряд сходится.
то по признаку Даламбера исследуемый ряд сходится.
Признак сравнения
Пусть даны два ряда с положительными членами
 … (а)
… (а)
 … (б)
… (б)
если начиная с некоторого номера n:
1)  и ряд (б) сходится, то и ряд (а) также сходится;
и ряд (б) сходится, то и ряд (а) также сходится;
2)  и ряд (б) расходится, то и ряд(а) также расходится.
и ряд (б) расходится, то и ряд(а) также расходится.
При использовании этого признака исследуемый ряд часто сравнивается либо с бесконечной геометрической прогрессией  , которая при
, которая при  сходится, а при
сходится, а при  расходится, либо с гармоническим рядом.
расходится, либо с гармоническим рядом.
Пример 9
Исследовать ряд на сходимость с помощью признака сравнения 
Решение:
Каждый член  данного ряда, начиная со второго, больше соответствующего члена гармонического ряда:
данного ряда, начиная со второго, больше соответствующего члена гармонического ряда: 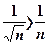 , и, так как гармонический ряд расходится, то, согласно признаку сравнения, исходный ряд также расходится.
, и, так как гармонический ряд расходится, то, согласно признаку сравнения, исходный ряд также расходится.
Знакопеременные ряды
Если знаки членов ряда (1) строго чередуются, то ряд называется знакочередующимся (знакопеременным).
Знакопеременный ряд  (2) называется абсолютно сходящимся если ряд,
(2) называется абсолютно сходящимся если ряд,
 (3), составленный из абсолютных значений его членов сходится.
(3), составленный из абсолютных значений его членов сходится.
Знакопеременный сходящийся ряд (2) называется условно сходящимся, если ряд (3) расходится.
|
|
|
Всякий абсолютно сходящийся ряд есть ряд сходящийся.ъ
Признак Лейбница
Знакочередующийся ряд  ,
,  сходится, если его члены убывают по абсолютному значению, стремясь к нулю, т.е. если
сходится, если его члены убывают по абсолютному значению, стремясь к нулю, т.е. если  и
и 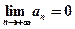 .
.
Пример 10. Доказать сходимость ряда 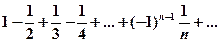
Решение:
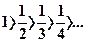 ,
, 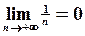 . Условия признака Лейбница выполняются, следовательно ряд сходится.
. Условия признака Лейбница выполняются, следовательно ряд сходится.
Функциональные ряды
Ряд 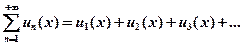 , члены которого являются функциями от переменной
, члены которого являются функциями от переменной  , называется функциональным.
, называется функциональным.
При различных значениях  получаются различные числовые ряды, которые могут быть сходящимися или расходящимися.
получаются различные числовые ряды, которые могут быть сходящимися или расходящимися.
Совокупность значений  , при которых функциональный ряд сходится, называется его областью сходимости.
, при которых функциональный ряд сходится, называется его областью сходимости.
Из всех функциональных рядов простейшими и наиболее употребительными являются степенные ряды вида
 (4)
(4)
или 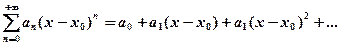 (5)
(5)
Областью сходимости всякого степенного ряда является интервал числовой оси, симметричный относительно точки  (для ряда (4)) или
(для ряда (4)) или 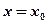 (для ряда (5)), который может быть закрытым, открытым или полуоткрытым.
(для ряда (5)), который может быть закрытым, открытым или полуоткрытым.
Для определения области сходимости обычно вначале используется признак Даламбера, а затем те значения  , для которых этот признак не решает вопроса о сходимости ряда, исследуется с помощью других признаков сходимости
, для которых этот признак не решает вопроса о сходимости ряда, исследуется с помощью других признаков сходимости
Пример 11. Найти область сходимости ряда 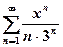 .
.
Решение:
 далее по признаку Даламбера ищем
далее по признаку Даламбера ищем

и определяем, при каких х этот ряд будет сходиться:  .
.
При  получаем ряд
получаем ряд  , который сходится по признаку Лейбница (см. пример 10).
, который сходится по признаку Лейбница (см. пример 10).
При 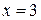 получаем гармонический ряд, который, как известно, расходится. Таким образом, интервалом сходимости данного степенного ряда является полуоткрытый интервал
получаем гармонический ряд, который, как известно, расходится. Таким образом, интервалом сходимости данного степенного ряда является полуоткрытый интервал  .
.
Ряды Тейлора
Рядом Тейлора для функции  в окрестности точки а называется степенной ряд относительно (х-а):
в окрестности точки а называется степенной ряд относительно (х-а): 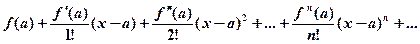
При а =0 ряд Тейлора есть степенной ряд относительно независимой переменной х: 
который принято называть рядом Маклорена.
Разложение в ряд Маклорена некоторых функций





Применение рядов к приближенным вычислениям
Для вычисления приближенных значений функций с заданной точностью удобно пользоваться рядами в том случае, когда соответствующий ряд является знакочередующимся; для знакочередующегося ряда легко оценить погрешность приближенного значения суммы - она меньше абсолютного значения первого из отброшенных членов.
|
|
|
Пример 12. Вычислить  с точностью до 0,001.
с точностью до 0,001.
Решение:
Разложим подынтегральную функцию  в степенной ряд и затем почленно проинтегрируем полученный сходящийся ряд в указанных пределах.
в степенной ряд и затем почленно проинтегрируем полученный сходящийся ряд в указанных пределах.
Заменив в разложении функции  , получим искомое разложение:
, получим искомое разложение:

Следовательно,

= 
 Полученный знакочередующийся ряд удовлетворяет условиям признака Лейбница. Так как шестой член этого ряда по абсолютной величине меньше 0,001, то достаточно взять сумму первых пяти членов.
Полученный знакочередующийся ряд удовлетворяет условиям признака Лейбница. Так как шестой член этого ряда по абсолютной величине меньше 0,001, то достаточно взять сумму первых пяти членов.
 Итак,
Итак, 
Варианты индивидуальных заданий
Задание 1.
Найти общий интеграл уравнения
.
1. 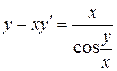 .
.
2. 
3. 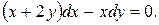
4. 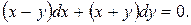
5. 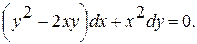
6. 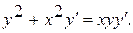
7. 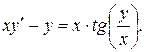
8. 
9. 
10. 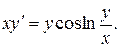
11. 
12. 
13. 
14. 
15. 
16. 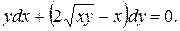
17. 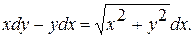
18. 
19. 
20. 
Задание 2.
Найти частное решение (частный интеграл) уравнения.
1. 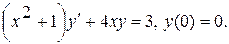
2. 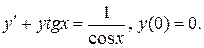
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 
13. 
14. 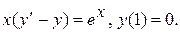
15. 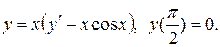
16. 
17. 
18. 
19. 
20. 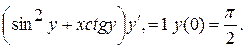
Задание 3.
Найти общее решение дифференциального уравнения.
1. 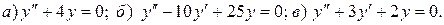
2. 
3. 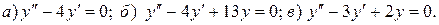
4. 
5. 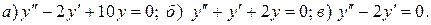
6. 
7. 
8. 
9. 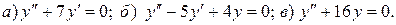
10. 
11. 
12. 
13. 
14. 
15. 
16. 
17. 
18. 
19. 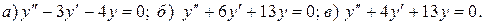
20. 
Задание 4.
Найти общее решение дифференциального уравнения.
1.  11.
11. 
2.  12.
12. 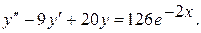
3.  13.
13. 
4.  14.
14. 
5.  15.
15. 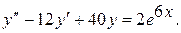
6.  16.
16. 
7.  17.
17. 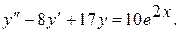
8.  18.
18. 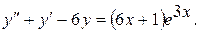
9. 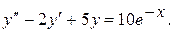 19.
19. 
10. 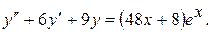 20.
20. 
Задание 5.
Написать три первые члены ряда. Найти интервал сходимости и исследовать ряд на сходимость на концах интервала.
1. 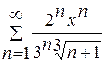 .
.
2.  .
.
3. 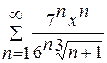 .
.
4. 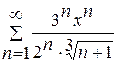 .
.
5.  .
.
6.  .
.
7.  .
.
8.  .
.
9.  .
.
10.  .
.
11.  .
.
12.  .
.
13.  .
.
14.  .
.
15.  .
.
16.  .
.
17.  .
.
18.  .
.
19.  .
.
20. 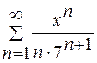 .
.
Задание 6.
Вычислить определенный интеграл с точностью до 0,001 путем разложения подынтегральной функции в ряд и почленного интегрирования этого ряда.
1. 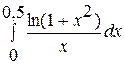 . 2.
. 2.  .
.
3.  . 4.
. 4.  .
.
5.  . 6.
. 6.  .
.
7.  . 8.
. 8.  .
.
9.  . 10.
. 10.  .
.
11.  . 12.
. 12. 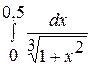 .
.
13. 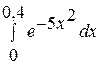 . 14.
. 14. 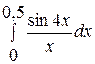 .
.
15.  . 16.
. 16.  .
.
17.  . 18.
. 18. 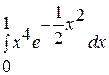 .
.
19. 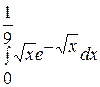 . 20.
. 20.  .
.
Библиографический список
1. Пискунов Н.С. Дифференциальное и интегральное исчисления: Учеб. пособие: В 2-х т. – Изд. стереотип. – М.: Интегралпресс. Т. 1. – 1991. – 416 с.
2. Шипачев В.С, Высшая математика: Учеб./под ред. А.Н. Тихонова. – 2-е изд. стереотип. – М.: Высш. шк., 1990. – 479 с.
3. Письменный Д.Т. Конспект лекций по высшей математике. I, IIч.. –М.:Рольф, 2002. – 288с.
4. Зайцев И.А. Высшая математика: Учеб. – М.: Высш. шк., 1991. – 400с.
5. Берман Г.Н. Сборник задач по курсу математического анализа: Учеб. пособие. – 20-е изд. – М.: Наука, 1985. – 416 с.
6. Данко П.Е. и др. Высшая математика в упражнениях и задачах: В 2ч. – М.: Высш. шк. т.1. – 1999. – 304 с.
7. Шипачев В.С. Задачник по высшей математике: Учеб. пособие. – 2-е изд., испр. – М.: Высш. шк., 2000. – 304 с.
Лицензия РБ на издательскую деятельность №0261 от 10 апреля 1998 года
|
|
|
Подписано в печать __________2006г. Формат. Бумага типографская. Гарнитура Таймс. Усл. печ. л._____. Усл. изд. л._____. Тираж______экз. Заказ №____.
Издательство Башкирского Государственного Аграрного Университета.
Типография Башкирского Государственного Аграрного Университета.
Адрес издательства и типографии: 450001, г. Уфа, ул. 50 лет Октября, 34.
|
|
|


