 |
Схема установки для определения модуля Юнга
|
|
|
|
Цель: Изменяя значение деформирующей силы определить модуль Юнга стальной проволоки.

Рабочая формула:
где  - модуль Юнга;
- модуль Юнга;  - начальная длина проволоки;
- начальная длина проволоки;  - удлинение
- удлинение
проволоки; 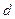 - диаметр проволоки,
- диаметр проволоки,  - расстояние от проволоки до линейки;
- расстояние от проволоки до линейки;  - расстояние от проволоки до оси качания зеркала; Fi = mig - деформирующая сила; mi – масса груза; g – ускорение свободного падения;
- расстояние от проволоки до оси качания зеркала; Fi = mig - деформирующая сила; mi – масса груза; g – ускорение свободного падения;  - деление на линейке, соответствующее недеформированной проволоке;
- деление на линейке, соответствующее недеформированной проволоке;  - деления на линейке, соответствующие определенной деформирующей силе;
- деления на линейке, соответствующие определенной деформирующей силе;
ВЫПОЛНЕНИЕ РАБОТЫ
1. Выбрать угол зрения так, чтобы видеть в зеркальце изображение линейки. Зафиксировать значение  , соответствующее недеформированной проволоке.
, соответствующее недеформированной проволоке.
2. Последовательно нагружая грузами проволоку, т.е. меняя значение деформирующей силы  , определить значения
, определить значения  .
.
3. Провести аналогичные измерения, разгружая проволоку.
4. Полученные данные использовать для вычисления модуля Юнга по рабочей формуле. Значения  ,
,  ,
, 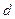 приведены на стенде к лабораторной работе.
приведены на стенде к лабораторной работе.
5. Данные занести в таблицу, определить погрешность измерений.
6. Полученный результат сравнить с табличным значением модуля Юнга для стали Ест = 20 х 1010 Па.
Таблица результатов: Определение модуля Юнга
| № | 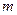 кг
кг
|  ,
м ,
м
| 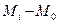 ,
м ,
м
|  , м , м
|  ,
Па ,
Па
| 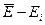
| 
| 
|  , % , %
|
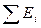
| 
|
Обработка результатов:
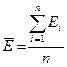
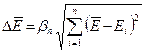

|
|
|
Вывод:
Результат: 
 % Еэксп.
% Еэксп.  Етабл
Етабл
Лабораторная работа № 5
ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ
ТВЕРДОГО ТЕЛА
Вопросы для подготовки:
Твердое тело, как система материальных точек. Ось вращения. Обращение материальной точки вокруг неподвижной оси. Центр масс.
Момент силы. Момент инерции.
Основное уравнение динамики вращательного движения.
Теорема Штейнера.
Момент количества движения. Импульс момента силы. Закон изменения момента количества движения.
Закон сохранения момента количества движения.
Кинетическая энергия вращающегося тела.
Физический маятник и его характеристики.
ОПИСАНИЕ УСТАНОВКИ

Исследуемое тело представляет собой диск, в котором имеются отверстия для подвешивания на ось. С – центр тяжести тела.
При отклонении тела от положения равновесия возникает возвращающая сила, которая стремится вернуть тело в первоначальное положение.
Схема установки для определения момента инерции
Вследствие инерции тело проходит положение равновесия и отклоняется в противоположную сторону. Возникают гармонические колебания.
Цель: Используя законы динамики вращательного движения и характеристики колебаний физического маятника, определить момент инерции диска относительно оси вращения, проходящей через центр масс.

Рабочая формула:
где I - момент инерции; Т - период колебаний диска; m - масса диска, g - ускорения свободного падения,  - расстояние от оси качания до центра масс С.
- расстояние от оси качания до центра масс С.
ВЫПОЛНЕНИЕ РАБОТЫ
1. Подвесить диск на одну из осей вращения, предварительно измерив расстояние  от центра масс С до данной оси вращения.
от центра масс С до данной оси вращения.
2. Отклонить диск от положения равновесия на небольшой угол, вызвав колебательное движение.
3. Измерить время t колебаний диска (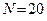 ) для данной оси вращения.
) для данной оси вращения.
4. Определить период колебаний  . Опыт повторить пять раз.
. Опыт повторить пять раз.
5. Полученные данные использовать для вычисления момента инерции диска относительно данной оси по рабочей формуле. Значение массы диска m приведено на стенде к лабораторной работе.
|
|
|
6. Применяя теорему Штейнера, вычислить момент инерции Ic относительно оси, проходящей через центр масс диска,
7. Данные занести в таблицу, определить погрешность измерений.
8. Вычислить теоретическое значение момента инерции для данного диска 
9. Сравнить полученный результат 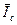 с теоретическим
с теоретическим  .
.
Таблица результатов: Определение момента инерции твердого тела
| № |  ,
м ,
м
|  ,
с ,
с
|  , с , с
| 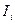

| 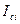

| 
| 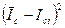
| 
|  , % , %
|

| 
|
Обработка результатов:
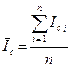


Вывод:
Результат: 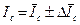
 %
%  эксп.
эксп. 
 теор.
теор.
Лабораторная работа № 6
|
|
|


