 |
Моделирование неприрывных случайных воздействий
|
|
|
|
1. ЦЕЛЬ И ЗАДАЧИ РАБОТЫ
Освоение методов получения реализаций непрерывной случайной величины на ЭВМ. Имитация случайных воздействий по заданному закону на ЭВМ.
2. ОСНОВЫ ТЕОРИИ
При построении имитационных моделей часто возникает необходимость в получение реализаций разного рода случайных величин: промежутков времени между некоторыми событиями, воздействий некоторых физических величин на систему управления, размеров обрабатываемых деталей и т.п.
Для формирования возможных значений случайных величин с заданным законом распределения исходным материалом служат обычно случайные величины, имеющие равномерное распределение в интервале [0,1].
Для получения реализаций непрерывной случайной величины X с заданной плотностью распределения вероятностей f(x) существует немало искусственных приёмов. Они достаточно полно излагаются в [2]. Из этих методов весьма распространен метод нелинейного преобразования, называемым методом обратной функции. Этот метод основан на использовании соотношения
, i=1,2,…
в котором ui - i-я реализация случайной величины U, равномерно распределённой в интервале [0,1]; xi - i-я реализация случайной величины X, описываемой плотностью вероятности f x).
При использовании интегральной функции распределения вероятностей P[x<xi]=F(xi) получаем уравнение
F(xi)=ui, i=1,2,3,...,
решение которого относительно xi даёт явную функциональную связь между xi и ui: xi=F-1(ui).
В некоторых случаях метод обратной функции легко алгоритмизируется и даёт явное выражение для расчёта искомой случайной величины с заданным законом распределения вероятностей.
Равномерное распределение
Для имитации равномерного распределения на интервале от a до b используют обратное преобразование соответствующей функции распределения, которое приводит к выражению
|
|
|
x= a + (b-a) u,
где u - случайные числа, полученные от ДСЧ.
Экспоненциальное распределение
Когда вероятность наступления события в малом интервале времени Dt очень мала и не зависит от наступления других событий, то интервалы времени между последовательными событиями распределяются по экспоненциальному закону с плотностью вероятностей
, m £ t <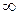 
, (m=const).
Этому закону распределения подчиняются многие явления, например, длительность телефонных разговоров, срок службы многих электронных деталей, время поступления заказов на предприятие и т.д.
Для имитации экспоненциального распределения используют обратное преобразование функции плотности
T = -(l/ 
) ln u + m,
где u - случайные числа, получаемые от ДСЧ.
Метод обратных функций позволяет формально записать формулы для моделирования любой случайной величины. Однако довольно часто невозможно аналитическое определение обратной функции. В подобных случаях используют специальные методы моделирования. Используют либо специальные законы теории вероятностей, либо особенности моделируемого закона распределения вероятностей. К числу подобных подходов относится и подход при моделировании нормально распределённой случайной величины.
Нормальное распределение
Нормальное, или гауссово распределение - один из наиболее важных и часто используемых видов распределения.
Все известные методы генерирования нормально распределенных случайных чисел основаны на преобразовании Z=(X-a)/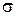 
, где a - математическое ожидание, 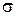-среднеквадратическое отклонение. В этом случае случайная величина Z распределена нормально с математическим ожиданием равным 0 и среднеквадратическим отклонением равным 1 (её называют стандартной случайной величиной, описываемой плотностью распределения
|
|
|
Переход к требуемому нормальному распределению осуществляется соотношением X=a+Z ).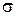
Достаточно эффективным подходом к моделированию стандартной нормально распределённой случайной величины является алгоритм Марсальи-Брея, быстро дающий точные результаты. По этому алгоритму генерируются два случайных числа u1 и u2. Далее полагая V1=-1+2u1 и V2=-1+2u2, вычисляют S=V12+V12. При S³1 начинают цикл снова.
При S<1 вычисляются
.
Для генерирования 100 пар нормально распределённых случайных чисел понадобится в среднем 127 пар случайных чисел (U1 и U2).
Алгоритм генерирования стандартных нормальных случайных величин приведен на рис.3.1. Алгоритм может быть оформлен в виде процедуры с формальными параметрами (EX, SKO, X1, X2).
процедура NORMAL (EX,SKO,X1,X2)
1 V1=2*RANDОM - 1
V2=2*RANDOM - 1
S=V1*V1+V2*V2
Если (S ³ 1.0) идти к 1
SQ=SQRT(-2*ALOG(S))/S)
R1=V1*SQ
R2=V2*SQ
X1=EX+R1*SKO
X2=EX+R2*SKO
Возврат в точку вызова
Конец
Рис.3.1. Программа генератора нормально распределённых случайных величин
Исходными данными здесь являются математическое ожидание EX и среднеквадратическое отклонение SKO. За одно обращение к программе получаются два нормально распределённых случайных числа X1 и X2.
Логарифмически-нормальное распределение
Случайная величина X имеет логарифмически-нормальное распределение, если величина Y= ln(X-A) распределена по нормальному закону. Величина A является параметром этого закона распределения вместе с параметрами a и σ нормального закона для Y. Плотность распределения случайной величины X задаётся формулой
.
Математическое ожидание и дисперсия определяются по формулам
M[X]=A+exp(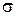 2/2 + a), D[X] = (exp( 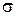2)-1) exp( 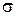2+2a).
Используя связь X и Y, получаем следующий способ имитации логарифмически - нормально распределённой случайной величины X:
1) имитируется стандартная нормальная величина Y;
2) вычисляется X=A + exp(Y).
Гамма-распределение
Гамма-распределение является одним из наиболее полезных видов непрерывных распределений в имитационном моделировании. Если величины, характеризующие какое-либо случайное явление, не могут принимать отрицательных значений, то, скорее всего, такое явление наиболее удачно может имитироваться с помощью гамма - распределения.
Это распределение описывается двумя параметрами, 
и 
, где характеризует форму, а 
-масштаб распределения (рис.3.2).
|
|
|
Рис. 3.2. Гамма-распределение.
При изменении этих параметров плотность гамма-распределения -
где >0, =0 X>0, математическое ожидание M[X]= / дисперсия D[X]= / 2, может принимать самую различную форму, что делает его одним из наиболее универсальных видов распределений для построения различных видов моделей.
На рис.3.3 показан алгоритм достаточно удобного двухпараметрического гамма - генератора Филлипса [1] GAMMA с формальными параметрами (ALPHA, BETA, START, X).
Значения ALPHA, BETA и начальное значение START (целое число менее 1,5) являются исходными данными.
Для определения значений параметров гамма - распределения можно воспользоваться уравнением
=M2[X]/D[X]; =M[X]/D[X].
Гамма-распределение связано с целым рядом других полезных распределений. Например, если =1 и =const, то генерируется экспоненциальная функция плотности. Если α принимает целочисленное значение K, то получим распределение Эрланга-К. Если =v/2 и =2 (где v -число степеней свободы), получается распределение хи-квадрат. Могут быть получены и другие виды распределений.
Процедура GAMMA (ALPHA,BETA,START,X);
Если (START³1.5) идти к 60;
X3=1.0;
Если (ALPHA£1.5) идти к 1;
Если (ALPHA£19.0) идти к 2;
Идти к 3;
1 B=0.24797+(1.34735740*ALPHA)-(0.00004204*ALPHA**2)+
(0.53203176*ALPHA**3)-(0.13671536*ALPHA**4)+(0.01320864*ALPHA**3);
Идти к 4;
2 B=0.64350+(0.45839602*ALPHA)-(0.02952801*ALPHA**2)+(0.00172718
*ALPHA**3)-(0.00005810*ALPHA**4)+(0.00000082*ALPHA**5);
идти к 4;
3 B=1.33408+(0.22499991*ALPHA)-(0.00230695*ALPHA**2)+
(0.00001623*ALPHA**3)-(0.00000006*ALPHA**4);
4 Y=1.0+(1.0/B);
START=5.0;
12 Если (Y-1.0 <0) то 110;
Если (Y-1=0), то 50;
15 Y=Y-1.0;
X3=X3*Y;
Идти к 12
110 GY=1.0+Y(-0.5771017+Y*(0.985854+Y*(-0.8764218+Y*
(0.8328212+Y*(-0.5684729+Y*(0.2548205+Y*(-0.05143930)))))));
X3=X3*GY/Y;
50 A=(X3/(ALPHA*BETA))**B;
B=1.0/B;
A=1.0/A;
60 X=(-A*ALOG(URAND(IX)))**B;
Возврат в точку вызова
Конец.
Рис.3.3. Алгоритм генератора для случайных величин, подчиняющихся гамма - распределению с параметрами ALPHA и BETA (X-случайная величина, имеющая гамма-распределение).
3. ОБЪЕКТЫ И СРЕДСТВА ИССЛЕДОВАНИЯ
Объектами исследования в лабораторной работе являются программные генераторы случайных величин, распределённых по заданному закону.
|
|
|
Исследование генераторов и использование их для имитации случайных воздействий проводится с помощью ПЭВМ.
Используемый язык программирования – любой универсальный.
4. ПОДГОТОВКА К РАБОТЕ
4.1. Ознакомится с методами получения реализаций случайных величин с заданным законом распределения вероятностей.
4.2. Ознакомится с генераторами случайных величин, распределённых по равномерному, экспоненциальному, нормальному, логарифмически-нормальному и гамма законам.
4.3. Повторить выбранный для работы язык программирования.
5. ПРОГРАММА РАБОТЫ
5.1. Составить схему алгоритма и программу для имитации случайной величины X, распределённой по заданному закону.
Варианты законов распределения случайной величины X:
1) равномерное распределение;
2) экспоненциальное распределение;
3) нормальное распределение;
4) логарифмически-нормальное распределение;
5) гамма-распределение.
Параметры законов распределения могут быть выбраны произвольно. Программу оформить в виде стандартной подпрограммы.
5.2. Составить схему алгоритма и написать программу вычисления вероятности события
M[X]-1/k£X£M[X]+1/k,
где k-номер студента по списку группы, X-случайная величина с заданными в п.5.1 законами распределения. При составлении программы рекомендуется использовать написанную в соответствие с п.5.1 подпрограмму для вычисления значения X. Используя 10000 реализаций X, вывести на печать 30 первых значений случайной величины, гистограмму распределения и значение частоты попадания в указанный выше интервал. Сравнить эту частоту с теоретической вероятностью.
6.КОНТРОЛЬНЫЕ ВОПРОСЫ
6.1. Какие методы используются для формирования значений случайной величины с заданным языком распределения?
6.2. В чём состоит сущность метода обратной функции?
6.3. Привести алгоритм имитации равномерного и экспоненциального распределений.
6.4. Изложить алгоритмы имитации случайной величины по нормальному и логарифмически-нормальному законам распределения.
6.5. Чем объясняется разница между теоретической вероятностью и частотой попадания исследуемой в лабораторной работе величины X в заданный интервал её значений?
Лабораторная работа 5
ИМИТАЦИЯ ПОТОКОВ СОБЫТИЙ
1. ЦЕЛЬ И ЗАДАЧИ РАБОТЫ
Освоение методов моделирования потоков событий. Имитация потока входных заявок в системах массового обслуживания.
2. ОСНОВЫ ТЕОРИИ
Потоком событий называют последовательность однородных событий, появляющихся одно за другим в случайные моменты времени. Примеры: поток вызовов на телефонной станции; поток забитых шайб при игре в хоккей; поток автомобилей на АЗС; поток заявок на предприятиях бытового обслуживания и т.п. Имитацию потоков событий наиболее часто приходится проводить при исследовании систем массового обслуживания.
|
|
|
С потоком событий можно связывать различные случайные события, но не имеет смысла говорить о вероятностях "событий", образующих поток.
Поток событий случаен, поэтому вычислить можно только какую-то его конкретную реализацию.
Поток событий наглядно изображается рядом точек с абсциссами t1,t2,...,tj,...(например, последовательностью моментов времени, в которые в систему поступают заявки). При вероятностном описании поток событий может быть представлен последовательностью случайных величин-промежутков времени между последовательными событиями:
Z1=t1;
Z2=t2-t1;
Z3=t3-t2;
......;
Zj=tj-tj-1.
.......
Тогда последовательность случайных величин представляется следующим образом: t1, t2=t1+Z2, t3=t2+Z3 и т.д.
В общем случае для задания последовательности случайных величин Zm (m=1,2,3,...) требуется указать совместные функции распределения
F(x1,x2,...,xm) = P[Z1<x1,...,Zm<xm].
Такое описание очень громоздко, в связи с чем на практике используются частные типы потоков событий, допускающие более простое описание.
Наиболее часто используются стационарные потоки с ограниченным последствием. Для этих потоков вероятность попадания того или другого числа событий на любой интервал времени зависит только от длины этого интервала и не зависит от расположения интервала на оси времени, а сами интервалы Zj - независимые случайные величины с одинаковой плотностью расрпеделения fj(x)=f(x) (i=2,3,...).Плотность распределения f1(x)-момента поступления t1 первой заявки может отличается от f(x) и связана с ней формулой
где λ - интенсивность потока событий.
Способ моделирования стационарного потока с ограниченным последствием достаточно прост. Сначала получают реализацию случайной величины с плотностью f(x) и находят момент времени появления первого события – t1. Далее последовательно осуществляется следующая процедура. Пусть tj-момент наступления j-го события уже вычислен. Получаем реализацию Z случайной величины с плотностью распределения вероятностей f(x) и вычисляем момент tj+1 прихода очередного события: tj+1=tj+Z и т.д.
Рассмотрим конкретные, часто используемые, типы потоков и способы их имитации.
|
|
|
