Исследование свойств системы массового обслуживания

 

1. ЦЕЛЬ И ЗАДАЧИ РАБОТЫ.

Исследование основных характеристик простейших систем массового обслуживания методом имитационного моделирования. Алгоритмизация функционирования системы, организация и проведение машинного эксперимента, обработка данных. Развитие творческого подхода к комплексному исследованию.

 

2. ОСНОВЫ ТЕОРИИ.

Системой массового обслуживания называется любая система, предназначенная для обслуживания каких - либо заявок (требований), поступающих на неё в случайные моменты времени. Примеры систем массового обслуживания (СМО): телефонная станция, бюро ремонта, билетная касса, парикмахерская, ЭВМ и др.

Любое устройство, непосредственно занимающееся обслуживанием заявок, называется каналом обслуживания (или) прибором. СМО - бывают как одно - так и многоканальными. Пример одноканальной СМО - билетная касса с одним кассиром; пример многоканальной - та же касса с несколькими кассирами.

Различают СМО с отказами и СМО с очередью (ожиданием). В СМО с отказами заявка, пришедшая в момент времени, когда все каналы заняты, получает отказ, покидает СМО и в дальнейшей ее работе не участвует. В СМО с очередью заявка, пришедшая в момент занятости всех каналов, не покидает СМО, а становится в очередь и ждет, пока не освободится какой-нибудь канал. Число мест в очереди может быть как ограниченным, так и неограниченным. При нулевом числе мест в очереди СМО с очередью превращается в СМО с отказами. Очередь может иметь ограничение и по времени ожидания заявки. Такие СМО называются системами с нетерпеливыми клиентами.

СМО с очередью различаются не только по ограничению очереди, но и по дисциплине обслуживания: обслуживаются ли заявки в порядке поступления или в случайном порядке, или же некоторые заявки обслуживаются вне очереди (так называемые СМО с приоритетом). Приоритет может иметь несколько уровней или рангов.

Многофазная СМО представляет собой последовательность обслуживающих приборов (фаз). При этом входной поток заявок последующей фазы является выходным потоком предыдущей фазы.

Описание СМО включает в себя три основных момента:

1. Описание входного потока заявок (событий). Исследование СМО упрощается, если потоки событий простейшие (стационарные пуассоновские). Для СМО это допущение означает, что как поток заявок, так и поток обслуживания - простейшие. потоком обслуживания понимают поток заявок, обслуживаемым одна за другой одним непрерывно занятым каналом. Этот поток оказывается простейшим, только если время обслуживания представляет собой случайную величину, имеющую показательное распределение. Вместо "поток обслуживания - простейший" часто говорят "время обслуживания - показательное". В дальнейшем обозначим t_пост - момент поступления заявки в СМО.

2. Описание обслуживающих приборов (каналов). Определяется количество каналов, время обслуживания заявки - случайная величина с заданным законом распределения.

3. Описание дисциплины обслуживания, т.е. правил по которым выбирается на обслуживание очередная заявка. Например, заявки обслуживаются в порядке их поступления. Если поступившая заявка застаёт канал занятым, то она ожидает освобождение канала в течение времени _ож. Если за это время канал не освободится, заявка покидает систему не обслуженной. Время _ож - случайная величина с известным законом распределения.

Кроме указанных для описания СМО, могут быть использованы и другие величины, например, t_св - момент освобождения канала после обслуживания очередной заявки, t_н - момент начала обслуживания, t_ух - момент ухода заявки из системы, _рем - время ремонта канала и д.р.

Задачи исследования СМО - нахождение вероятностей различных состояний СМО, а также установление зависимости между заданными параметрами и характеристиками эффективности работы СМО. В качестве таких характеристик могут рассматриваться, например, следующие:

среднее число заявок А, обслуживаемое СМО в единицу времени, или абсолютная пропускная способность СМО;

вероятность обслуживания поступившей заявки Q или относительная пропускная способность СМО; Q=A/ ;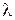

вероятность отказа P_отк, т.е. вероятность того, что поступившая заявка не будет обслужена: P_отк=1-Q;

среднее число заявок, получающих отказ за промежуток времени [0,T];

среднее число заявок в СМО (обслуживаемых или ожидающих в очереди);

среднее время пребывания заявки в СМО (в очереди или под обслуживанием);

среднее число занятых каналов и д.р.

Рассмотрим несколько типовых схем моделирования СМО, которые легко могут быть модифицированы для конкретных случаев.

На рис. 6.1. представлена схема моделирования однолинейной СМО с ожиданием. Целью моделирования является подсчёт числа заявок получающих отказ за промежуток времени (0, Т), и времени ожидания обслуживания для обслуженных заявок. На схеме показана только фиксация этих величин, предполагая, что они обрабатываются одним из статистических методов. Эта схема легко модифицируется для СМО с неограниченным ожиданием. В первом случае удаляется вся левая половина схемы, во - втором, удаляются блоки 6 и 7.

< A1. Алгоритм моделирования одноканальной СМО с ожиданием>

1. t_св = 0, счетчики установить в “0”;

2. Формирование t_пост;

3. Если t_пост > T то 14;

4. Если t_пост £ t_св идти к 5, иначе 10

5. Формирование _ож

6. t_ух = t_пост + _ож ;

7. Если t_ух < t_осв , то (t_н = t_св. Идти к 9);

8. Подсчет не обслуженных заявок;

9. t_H = t_св; идти к 11;

10. t_H = t_пост;

11. Формирование ;

12. tсв=tсв+ ;

13. Если t_cb£T то “Ожидание t_n-t_пост число обслуживаемых заявок” иначе 8;

14.“Обработка результатов, оценка вариантов”;

15. КОНЕЦ

 

Рис. 6.1.Схема моделирования одноканальной СМО с ожиданием

Рис.6.2. Фрагмент схемы алгоритма моделирования СМО с ненадежным каналом обслуживания

На рис. 6.2. представлен фрагмент алгоритма, который при добавлении к схеме 6.1. превращают её в схему алгоритма для СМО с надёжной линией обслуживания. В такой СМО могут происходить сбои в случайные моменты времени t_сб. В результате сбоя обслуживание заявки прекращается. После сбоя в течении времени t_рем обслуживающий канал ремонтируется и будет вновь готов к работе в момент времени t_гот = t_сб+ _рем.Последовательность моментов сбоя t_сб имитируется как случайный поток. Величина a в схеме - признак формирования момента сбоя; при α=1 нужно формировать очередной поток сбоя.

На рис. 6.3. изображена схема алгоритма моделирования СМО с приоритетом обслуживания. Каждая заявка обладает определённым показателем приоритета, в качестве которого использована величина, обратная времени ожидания обслуживания t_ож.

Рис. 6.3. Схема алгоритма моделирования СМО с приоритетным обслуживанием

Если в момент освобождения канала имеется очередь ожидающих обслуживание заявок, то первой на обслуживание будет принята заявка с минимальным _ож. Информация о состоянии очереди задаётся в следующем виде: к - количество заявок в очереди, tⁱ_ух - момент времени ухода из системы i - й заявки, если до этого момента не произойдёт освобождение канала (i=1,2,...,к). Совокупность величин {tⁱ_ух} сортируется в убывающем порядке. Таким образом, номер самой нетерпеливой заявки равен к.

Для каждой заявки, приходящей до момента освобождения канала, определяется показатель приоритета t^к_ух и заявка вставляется в очередь (операторы 5 - 8). После освобождения канала просматривается очередь и из неё удаляются заявки, не дождавшиеся обслуживания (операторы 17 - 20). Как только обнаруживается заявка, у которой t_ух>t_св, то происходит переход к операторам обслуживания заявки (операторы 11 - 13).

После операторов обслуживания проверяется условие "к=0". При выполнении условия формируется момент времени поступления следующей заявки. Длина очереди увеличивается на единицу и происходит переход к следующему оператору.

Рассмотрим теперь некоторые особенности построения алгоритма моделирования многоканальной СМО.

Пусть СМО имеет n обслуживающих каналов. Предполагается, что время обслуживания зависит от номера канала. Для разных каналов это время является случайной величиной. Если заявка застаёт свободными несколько каналов, используются следующие варианты:

каналы занимаются в порядке их номеров, т.е. поступившая заявка занимает канал с наименьшим номером;

освободившийся канал встаёт в очередь и не занимается до тех пор, пока не будет занят освободившийся ранее канал;

каналы занимаются в случайном порядке, например, выбираются по жребию с вероятностью р=1/n_св, где n_св - число свободных каналов в момент прихода заявки.

На рис. 6.4 представлен один из возможных алгоритмов моделирования СМО с n каналами. В моделирующем алгоритме предположено, что при наличие нескольких свободных каналов заявка занимает канал с наименьшим номером.

Рис.6.4. Схема алгоритма моделирования многоканальной СМО

В схеме алгоритма приняты следующие обозначения: tⁱ_св - момент времени освобождения i - го канала, tⁱ_н - момент времени начала обслуживания на i - м канале (i=1,2,...,n), t_св - самый ранний из моментов tⁱ_св: t_св=min {tⁱ_св}.

При поступлении заявки в СМО в момент времени t_пост отыскивается освободившийся канал с помощью оператора сравнения t_пост<tⁱ_св. Как только для некоторого i окажется t_пост>tⁱ_св, то происходит переход на операторы 13-15 (см. рис. 3.4), имитирующие обслуживание в канале с номером i. Одновременно с просмотром массива {tⁱ_св} ищется его наименьший элемент t_св.

Если просмотрен весь массив и для всех i окажется, что tпост< 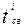, то это соответствует занятым каналам в момент поступления заявки, а ближайшее освобождение канала произойдет в момент t_св. Номер этого канала i_min. В этом случае работают операторы, вычисляющие момент ухода заявки tyx и вычисляется, дождется ли заявка освобождения канала или нет. Если да, то ее обслуживание происходит на канале с номером i_min, который является первым из освободившихся.

В заключение отметим особенность моделирования многофазной СМО. В общем случае входящий поток для такой системы имеет последствие. Однако, если на вход СМО с неограниченной очередью поступает простейший поток заявок, а время обслуживания показательное, то выходной поток системы будет простейшем, а интенсивность потока та же, что и входящего. Из этого следует, что многофазную СМО с неограниченной очередью перед каждой фазой, простейшим входящем потоком показательным временем обслуживания на каждой фазе можно представить как последовательность простых СМО.

 

3. ОБЪЕКТЫ И СРЕДСТВА ИССЛЕДОВАНИЯ

Объектами исследования в лабораторной работе являются промышленные комплексы и предприятия, городские службы и технические устройства, которые могут быть представлены как системы массового обслуживания.

Средством исследования является метод имитационного моделирования функционирования названных объектов, осуществляемый с помощью ЭВМ на одном из выбранных языков программирования высшего уровня. (В качестве языка программирования рекомендуется выбрать язык на котором были выполнены предыдущие лабораторные работы).

 

4. ПОДГОТОВКА К РАБОТЕ

4.1. Изучить основные понятия теории массового обслуживания.

4.2. Изучить методику описания объектов системами массового обслуживания.

4.3. Изучить основные характеристики эффективности СМО и способы их вычисления в процессе имитации функционирования системы.

4.4. Повторить методы имитации случайных величин и методы обработки результатов вычислений по материалам предыдущих лабораторных работ.

4.5. Иметь подпрограммы ДСЧ и имитации случайных величин с изученными ранее законами распределения.

 

5. ПРОГРАММА РАБОТЫ

5.1. Ознакомиться детально с описанием одной из предлагаемых ниже СМО.

Варианты СМО:

5.1.1. Одноканальная СМО с отказами представляет собой одну телефонную линию, на вход которой поступает простейший поток вызовов с интенсивностью =0,4 вызов/мин. Cредняя продолжительность разговора t_абсл=3 мин; время разговора имеет показательное распределение. Определить абсолютную и относительную пропускную способность СМО, а также вероятность отказа в обслуживании. Сравнить пропускную способность СМО с номинальной, которая была бы, разговор в точности длился бы три минуты, а заявки шли одна за другой непрерывно.

5.1.2. Железнодорожная сортировочная горка, на которую подаётся простейший поток составов с интенсивностью =2 состава в час, представляет собой одноканальную СМО с неограниченной очередью. Время обслуживания (роспуска) состава на горке имеет показательное распределение со среднем значением t_абсл=20 мин. Определить среднее число составов, связанных с горкой, среднее число составов в очереди, среднее время пребывания состава в СМО, среднее время пребывания состава в очереди.

5.1.3. Автозаправочная станция имеет две колонки (n=2). Площадка возле станции допускает одновременное ожидание не более 4 автомашин. Поток автомашин, прибывающих на станцию, простейший с интенсивностью =1 машина/мин. Время обслуживания автомашины - показательное со средним значением t_абсл=2 мин. Определить характеристики станции: абсолютную и относительную пропускные способности станции, вероятность отказа обслуживания, среднее число автомашин в очереди и в СМО, среднее время пребывания машин в очереди и в СМО, среднее число занятых каналов.

5.1.4. В зубоврачебном кабинете три кресла (n=3), а в коридоре имеются три стула для ожидания приёма. Поток клиентов - простейший с интенсивностью =1,2 клиента/час. Время обслуживания клиента - показательное со среднем значением t_абсл=20 мин. Если все три стула в коридоре заняты, клиент в очередь не становится. Определить среднее число клиентов, обслуживаемых кабинетом за час, среднюю долю обслуженных клиентов из числа пришедших, среднее число занятых стульев в коридоре, среднее время, которое клиент проведёт в коридоре и в кабинете.

5.1.5. СМО - билетная касса с одним окошком (n=1) и не ограниченной очередью. Касса продаёт билеты в пункты А и В. Пассажиров, желающих купить билет в пункт А, проходит в среднем трое за 20 мин, пункт В - двое за 20 мин. Поток пассажиров можно считать простейшим. Кассир в среднем обслуживает трёх пассажиров за 10 мин. Время обслуживания - показательное. Определить характеристики эффективности СМО: среднее число заявок в СМО, среднее число пассажиров в очереди, среднее время пребывания пассажиров в системе, среднее время простаивания пассажиров в очереди.

5.1.6. Одноканальная СМО - ЭВМ, на которую поступают заявки (требования на расчёты). Поток заявок - простейший со среднем интервалом между заявками t_ср=10 мин. Время обслуживания T_обсл распределено по закону Эрланга третьего порядка с математическим ожиданием t^ср_абсл=8 мин. Определить среднее число заявок в СМО и среднее число заявок в очереди, а также средние времена пребывания заявки в системе и в очереди.

5.1.7. Техническое устройство может время от времени выходить из строя. Поток отказов ТУ - простейший с интенсивностью =1,6 отказа в сутки. Время восстановления (ремонта) ТУ имеет равномерное распределение на участке от 0 до 1 суток. Определить среднюю долю времени, в течении которого ТУ работает.

5.1.8. СМО - обувной магазин в котором покупатели проходят три фазы обслуживания:

1) примерка и выбор обуви;

2) уплата денег в кассу;

3) получение покупки.

Поток покупателей простейший =45 человек/ч.

В отделе примерки имеется 4 стула. Среднее время примерки и выбора обуви равно 5 мин. Затем покупатель направляется в кассу, где вторично становится в очередь. Среднее время оплаты в кассе равно 1 мин. После оплаты покупатель идёт на контроль, где становится в новую очередь и получает покупку. На контроле работают три продавца. Среднее время выдачи покупки 2 мин. Все потоки событий - простейшие.

Рассматривая магазин как трёхфазную СМО, найти характеристики её эффективности: среднее число покупателей в очереди к первой, второй, третьей фазам обслуживания; среднее время пребывания покупателя в первой, второй, третьей фазах обслуживания; общее среднее число покупателей в магазине; общее среднее время затрачиваемое покупателями на приобретение обуви в магазине. В каком звене и как нужно улучшить обслуживание для того, чтобы сократить затраты времени покупателей?

5.1.9. На железнодорожную станцию поступает эрланговский 10-го порядка поток составов с интенсивностью =1,2 состава/час. Время обслуживания состава Т_обсл распределено в интервале от 0 до 1 ч по закону с плотностью =2(1-t) (0<t<1). Оценить характеристики эффективности станции: среднее число составов на станции, среднее время ожидания составом очереди на обслуживание.

5.1.10. Железнодорожная касса имеет два окошка, в каждом из которых продаются билеты в два пункта: Ленинград и Киев. Потоки пассажиров приобретающих билеты в Ленинград и в Киев по интенсивности одинаковы, =0,45 пасс./мин. Среднее время обслуживания пассажира 2мин. ступило рационализаторское предложение: для уменьшения очередей сделать обе кассы специализированными: в первой продавать билеты только в Ленинград, а во второй - только в Киев. Считая в первом приближении все потоки событий простейшими, проверить разумность этого предложения.

 

5.2. Построить математическую модель исследуемой СМО.

5.3. Составить моделирующий алгоритм функционирования СМО и вычисления искомых характеристик системы.

5.4. На одном из выбранных языков моделирования написать программу для проведения вычислительных экспериментов на ЭВМ.

5.5. Моделируя функционирование СМО на ЭВМ, оценить требуемые в задание характеристики эффективности системы.

5.6. Дать интерпретацию результатов вычислительных экспериментов с моделью СМО.

 

КОНТРОЛЬНЫЕ ВОПРОСЫ

6.1. Какие объекты называют СМО?

6.2. По каким признакам различают СМО?

6.3. Какова структура описания СМО?

6.4. Что понимается под характеристиками эффективности работы СМО? Назвать конкретные характеристики.

6.5. Что составляет предмет исследования СМО?

6.6. В чём состоят особенности моделирования многоканальных и многофазовых СМО?

6.7. Охарактеризовать метод, положенный в основу построения моделирующего алгоритма исследуемой СМО.

6.8. Объяснить, насколько удовлетворяют полученные характеристики исследованной СМО тем функциям, которые она должна была бы выполнять. Возможно ли улучшение характеристик СМО и какое?

 

Лабораторная работа 8

⇐ Предыдущая123456789Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: