 |
Задача 2 по теме «Оценка точности функций измеренных величин. Средняя квадратическая ошибка функции измеренных величин»
|
|
|
|
Б2.В.4 Математическая обработка земельно-кадастровой информации
МЕТОДИЧЕСКИЕ УКАЗАНИЯ И ЗАДАНИЯ
к лабораторным и контрольным работам для заочного отделения
«Землеустройство и кадастры»
Уфа 2014
УДК 378.147:004.02
ББК 74.58:32.973-018
М 54
Рекомендовано к изданию методической комиссией факультета землеустройства и лесного хозяйства
протокол № 7 от «06» мая 2014 г.
Составитель: доцент, к.п.н. Ардуванова Ф.Ф.
Рецензент: зав. кафедрой землеустройства, доцент, к.с.-х.н. Галеев Э.И.
Ответственный за выпуск:
зав. кафедрой математики, доцент, к.ф.-м.н. Лукманов Р.Л.
Методические указания к выполнению контрольной работы
Задача 1 по теме «Математическая обработка ряда независимых равноточных измерений»
Равноточными называют результаты, полученные при измерениях одним и тем же прибором, одним и тем же методом, одинаковым числом приёмов и в одинаковых условиях. Равноточные измерения характеризуются одинаковой для всех результатов средней квадратической ошибкой.
Пусть выполнен ряд равноточных измерений одной величины, истинное значение Х которой неизвестно. В результате измерений получены значения хi, свободные от систематических ошибок (это означает, что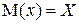 
).
Под математической обработкой ряда равноточных измерений понимают:
1. Определение наиболее надёжного значения измеряемой величины (наилучшей оценки неизвестного истинного Х), которым является простая арифметическая средина
 ,
|
где x 0 — наименьшее значение из ряда 
, 
;
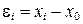2. Определение средней квадратической ошибки отдельного результата измерений по формуле Бесселя (оценка неизвестного параметра sx)
|
|
|
 ,
|
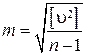где 
— уклонения от арифметической средины, которые обладают свойствами:
а) 
,
б)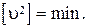 
3. Определение средней квадратической ошибки простой арифметической средины
 .
|
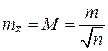Порядок обработки ряда равноточных измерений одной величины
Пример 1.1. Даны результаты равноточных независимых многократных измерений одного и того же угла. Определить: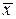 
, m, M, 
, 
.
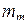| Таблица 1.1 | ||||||
| № П.п. | Результаты
измерений
| 
| 
| 
| 
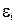
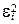
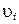
| Примечания |
| 67°33′44″ | +4 | –0,7 | 0,49 |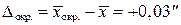 
Контроли:
а)  ;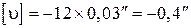
б)  .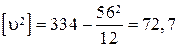
| ||
| 40″ | +0 | –4,7 | 22,1 | |||
| 43″ | +3 | –1,7 | 2,89 | |||
| 45″ | +5 | +0.3 | 0,09 | |||
| 46″ | +6 | +1,3 | 1,69 | |||
| 43″ | +3 | –1,7 | 2,89 | |||
| 48″ | +8 | +3,3 | 10,9 | |||
| 45″ | +5 | +0,3 | 0,09 | |||
| 48″ | +8 | +3,3 | 10,9 | |||
| 46″ | +6 | +1,3 | 1,69 | |||
| 47″ | +7 | +2,3 | 5,29 | |||
| 41″ | +1 | –3,7 | 13,7 | |||
| S | +56 | –0,4 | 72,72 |
1. Вычисление среднего арифметического
.
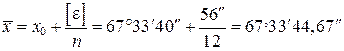В качестве наиболее надёжного значения принимаем среднее арифметическое, округлённое до десятых долей секунды
.
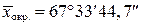2. Вычисление уклонений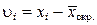 
, а также сумм 
, 
, 
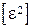непосредственно в таблице 3.1 и по контрольным формулам:
a)  ,
b)  .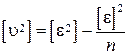
|
Расхождение между суммой , которую получили непосредственно в таблице, и её контрольным значением допускается в пределах (2–3)% от величины . Как видно из результатов вычислений (см. примечания в таблице 1.1), контроли выполнены.
3. Вычисление средней квадратической ошибки отдельного результата измерений по формуле Бесселя:
.
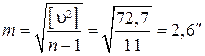4. Вычисление средней квадратической ошибки наиболее надёжного значения измеряемого угла:
.
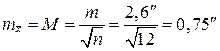5. Оценим точность полученных значений m и M по формулам:
 ,
 .
|
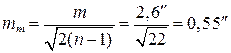Ответ: В сокращённой форме ответ имеет вид:
.
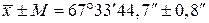Задача 2 по теме «Оценка точности функций измеренных величин. Средняя квадратическая ошибка функции измеренных величин»
В геодезии часто искомые величины находят в результате вычислений, как функции измеренных величин (аргументов). Очевидно, что ошибка функции будет зависеть как от ошибок измерения аргументов, так и от вида функции.
|
|
|
Пусть дана функция
 ,
|
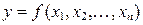где величины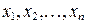 
— измерены независимо. Известны их средние квадратические ошибки 
.
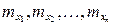Средняя квадратическая ошибка функции (2.1) вычисляется по формуле:
 .
|
Пример 2.1. В треугольнике измерены два угла, известны их средние квадратические ошибки 
, 
. Найти среднюю квадратическую ошибку третьего угла, вычисленного по двум измеренным.
Решение. Составляем функцию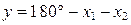 
; имеем:
; 
;
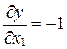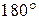— точное число; x 1 и x 2 — независимо измеренные углы.
Тогда по формуле имеем:
; 
.
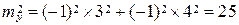Пример 2.2. Определить среднюю квадратическую ошибку превышения, вычисленного по формуле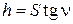 
, где S — горизонтальное проложение, n — угол наклона. Известно, что 
; 
; 
; 
; 
.
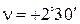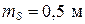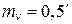Решение. Находим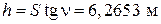 
и по формуле его среднюю квадратическую ошибку mh:
*),
где
; 
.
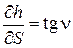Тогда
.
; 
; 
; 
.
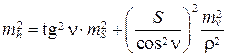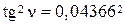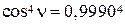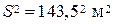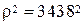Известно, что величина mh должна быть получена с двумя (или тремя, если число начинается с единицы) значащими цифрами. Чтобы это требование обеспечить, необходимо в промежуточных вычислениях по формуле удерживать в числах на одну значащую цифру больше, т.е. оставлять три (или четыре) значащие цифры, а сами числа следует представлять в стандартной форме. Например, число 0,043662 необходимо записать так: 
; число 34382 следует записать так: 
. Такие действия позволят упростить вычисления по формуле и, кроме того, дадут представление о величине влияния каждого источника ошибок на общую среднюю квадратическую ошибку функции.
С учётом сказанного выше находим:
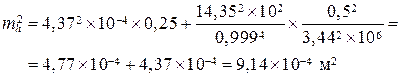
По результатам вычислений видно, что влияние линейных и угловых ошибок измерений в данной задаче примерно одинаково. Окончательно получаем:
.
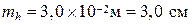Ответ: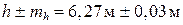 
.
|
|
|
