 |
Задача № 3 по теме «Оценка точности по разностям двойных измерений»
|
|
|
|
В геодезии часто приходится измерять большие группы однородных величин, причём каждую величину для контроля измеряют дважды.
Пусть однородные величины  измерены равноточно дважды и получены результаты измерений:
измерены равноточно дважды и получены результаты измерений:
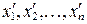 и
и 
Составим разности по формуле
 . .
| (3.1) |
Наиболее надёжные значения определяемых величин находим по формуле:
 . .
| (3.2) |
Для оценки точности используем разности (3.1).
а) При отсутствии систематических ошибок разности di можно рассматривать как истинные ошибки самих разностей, так как истинное значение разностей равно нулю ( ).
).
Применяя к ряду  формулу Гаусса, находим:
формулу Гаусса, находим:
 . .
| (3.3) |
Тогда средняя квадратическая ошибка отдельного результата измерений будет определяться по формуле:
 . .
| (3.4) |
Оценка точности наиболее надёжных значений определяется по формуле:
 . .
| (3.5) |
б) Если в результатах измерений присутствуют систематические ошибки, то величина

| (3.6) |
существенно отличается от нуля.
В этом случае из каждой разности необходимо исключить остаточное влияние систематических ошибок, вычесть систематическую ошибку из разностей, т. е.
 . .
|
Рассматривая разности  как уклонения от среднего
как уклонения от среднего  , применяя формулу Бесселя, находим
, применяя формулу Бесселя, находим
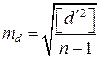 . .
| (3.8) |
Средние квадратические ошибки отдельного результата измерений и наиболее надёжных значений измеряемых величин находим по формулам:
 , ,
| (3.9) |
 . .
| (3.10) |
Заметим, что в этом случае необходимо выполнить контроль вычислений по формулам
a)  , где , где  ;
b) ;
b)  . .
| (3.11) |
Для определения значимости отклонения  от нуля применяют неравенство
от нуля применяют неравенство

| (3.12) |
Оценку точности начинают с проверки условия (3.12). Если, например, неравенство (3.12) выполняется, то делают вывод о том, что систематическими ошибками можно пренебречь и оценку точности следует выполнять по формулам (3.4–3.5).
|
|
|
Если неравенство (3.12) не выполняется, делают заключение о том, что систематическими ошибками пренебрегать нельзя, необходимо обработку вести по формулам (3.7, 3.9, 3.10)
Порядок обработки двойных равноточных измерений ряда
Пример 3.1. Одни и те же линии измерены дважды равноточно. Выполнить оценку точности по разностям двойных измерений.
| Таблица 3 | ||||||
| № |  (м) (м)
|  (м) (м)
|  (мм) (мм)
| 
| 
| 
|
| 120,389 | 120,380 | +9 | +6,3 | 39,7 | ||
| 136,468 | 136,462 | +6 | +3,3 | 10,9 | ||
| 133,223 | 132,229 | –6 | –8,7 | 75,7 | ||
| 124,536 | 124,537 | –1 | –3,7 | 13,7 | ||
| 140,457 | 140,449 | +8 | +5,3 | 28,1 | ||
| 143,682 | 143,688 | –6 | –8,7 | 75,7 | ||
| 139,158 | 139,149 | +9 | +6,3 | 39,7 | ||
| S | +0,1 | 283,5 | ||||


| ||||||

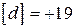
|
Решение:
1. Составим ряд разностей  .
.
2. Проверим условие (3.12). Согласно критерию обнаружения систематических ошибок вычисляем левую и правую части неравенства (3.12):
 ;
;  .
.
Вывод: левая часть неравенства (3.12) оказалась больше его правой части, следовательно, систематическими ошибками пренебрегать нельзя, т.е. систематическая ошибка присутствует.
3. Находим систематическую ошибку по формуле (3.6):
 ;
;  ,
,
затем исключаем его из каждой разности, находим  и суммы
и суммы  ,
,  ,
,  непосредственно в таблице 3 и выполняем контроль вычислений по формулам (3.11):
непосредственно в таблице 3 и выполняем контроль вычислений по формулам (3.11):
1.  : :
 , ,
 ; ;
| 2.  : :
 . .
|
Контроли выполнены.
4. Находим среднюю квадратическую ошибку одного измерения
 .
.
5. Определяем среднюю квадратическую ошибку наиболее надёжных значений измеряемых величин
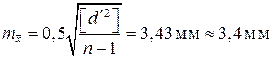 .
.
Требования к оформлению контрольной работы
1. Работа оформляется на листах формата А4.
2. К каждой задаче выписываются от руки необходимые формулы и прикладывается распечатка с расчетами в программе Microsoft Excel.
Задача №1
Даны результаты многократных независимых равноточных измерений одного и того же угла в таблице 1.
Выполнить математическую обработку данного ряда:
|
|
|
1. Определить простую арифметическую средину;
2. Вычислить среднюю квадратическую ошибку отдельного результата измерений (по формуле Бесселя);
3. Определить среднюю квадратическую ошибку арифметической средины;
Указания:
1) каждый студент исключает из таблицы, соответствующей варианту, три результата измерений, номера которых равны: i,  ,
,  , где i — номер варианта; у каждого студента в обработке будет 9 измерений;
, где i — номер варианта; у каждого студента в обработке будет 9 измерений;
2) все вычисления необходимо выполнять в соответствии со схемой решения примера 1.1 (среднее значение угла округлить до десятых долей сек.).
| Для вариантов 1-12 Таблица 1а | |||||
| № п/п | результаты измерений, хi | № п/п | результаты измерений, хi | № п/п | Результаты измерений, хi |
| 42°16′20,2″ | 42°16′20,4″ | 42°16′20,9″ | |||
| 22,8″ | 23,8″ | 22,5″ | |||
| 21,9″ | 24,2″ | 24,1″ | |||
| 20,8″ | 21,3″ | 21,8″ | |||
| Для вариантов 13-24 Таблица 1б | |||||
| № п/п | результаты измерений, хi | № п/п | результаты измерений, хi | № п/п | Результаты измерений, хi |
| 34°47′30,6″ | 34°47′35,2″ | 34°47′33,6″ | |||
| 32,7″ | 36,1″ | 33,8″ | |||
| 31,8″ | 34,2″ | 32,5″ | |||
| 30,5″ | 31,8″ | 35,8″ | |||
| Для вариантов 25-36 Таблица 1 в | |||||
| № п/п | результаты измерений, хi | № п/п | результаты измерений, хi | № п/п | Результаты измерений, хi |
| 57°51′23,6″ | 57°51′26,7″ | 57°51′22,9″ | |||
| 24,8″ | 24,3″ | 24,2″ | |||
| 28,4″ | 25,9″ | 25,1″ | |||
| 20,8″ | 22,3″ | 21,9″ |
Задача №2
В таблице 2 даны длины линии Si и дирекционные углы αi. Известны средние квадратические ошибки  и
и  . По одному из вариантов вычислить приращения координат по формулам:
. По одному из вариантов вычислить приращения координат по формулам:
 ,
, 
и их средние квадратические ошибки: 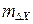 и
и 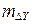 .
.
Указание: см. пример 2.2 (номер варианта выдается преподавателем).
| Таблица 2 | |||||||||
| № варианта | Si (м) | α i | № варианта | Si (м) | α i | № варианта | Si (м) | α i | |
| 215,04 | 32°30,0′ | 160,39 | 66°33,9′ | 219,24 | 34°30,6′ | ||||
| 123,48 | 43°45,0′ | 209,74 | 41°52,6′ | 125,45 | 33°45,8′ | ||||
| 178,85 | 34°10,5′ | 176,89 | 34°12,9′ | 173,83 | 44°10,5′ | ||||
| 187,57 | 55°22,4′ | 182,72 | 48°38,0′ | 182,56 | 35°22,4′ | ||||
| 192,44 | 37°48,6′ | 168,09 | 56°18,0′ | 195,42 | 27°48,6′ | ||||
| 267,74 | 32°30,8′ | 168,67 | 62°34,9′ | 216,89 | 32°31,2′ | ||||
| 183,78 | 43°34,6′ | 211,67 | 45°56,3′ | 127,43 | 53°45,5′ | ||||
| 189,85 | 34°13,6′ | 234,91 | 42°16,9′ | 172,12 | 24°10,5′ | ||||
| 156,27 | 52°24,8′ | 232,72 | 42°34,7′ | 184,34 | 15°22,4′ | ||||
| 243,04 | 26°42,3′ | 198,09 | 43°23,2′ | 192,91 | 67°48,6′ |
Задача № 3
|
|
|
Двенадцать линий измерены дважды независимо и равноточно (таблица 3). Произвести оценку точности по разностям двойных измерений:
1) вычислить среднюю квадратическую ошибку одного результата измерений;
2) среднюю квадратическую ошибку средних из результатов двойных измерений;
3) относительные средние квадратические ошибки.
Указания:
1) каждый студент исключает из таблицы, соответствующей варианту, три результата измерений, номера которых равны: i,  ,
,  , где i — номер варианта; у каждого студента в обработке будет 15 измерений;
, где i — номер варианта; у каждого студента в обработке будет 15 измерений;
2) все вычисления выполнить в соответствии со схемой решения примера 3.1.
| Для вариантов 1 ‑ 18 Таблица 3 | ||||||||
| № п/п | результаты измерений | № п/п | результаты измерений | № п/п x ″ (м) | результаты измерений | |||
| x ′ (м) | X ″ (м) | x ′ (м) | x ′ (м) | x ′ (м) | x ′ (м) | |||
| 124,855 | 124,842 | 191,379 | 191,365 | 191,387 | 191,379 | |||
| 143,021 | 143,011 | 147,370 | 147,362 | 169,370 | 169,372 | |||
| 160,384 | 160,387 | 175,772 | 175,754 | 275,756 | 275,762 | |||
| 156,475 | 156,486 | 192,277 | 192,268 | 342,257 | 342,277 | |||
| 128,355 | 128,365 | 140,318 | 140,336 | 156,245 | 156,254 | |||
| 150,687 | 150,676 | 168,812 | 168,821 | 188,892 | 188,888 |
| Для вариантов 19 ‑ 36 Таблица 3 | ||||||||
| № п/п | результаты измерений | № п/п | результаты измерений | № п/п x ″ (м) | результаты измерений | |||
| x ′ (м) | X ″ (м) | x ′ (м) | x ′ (м) | x ′ (м) | x ′ (м) | |||
| 534,855 | 534,843 | 595,379 | 595,365 | 595,364 | 595,379 | |||
| 543,035 | 543,055 | 547,370 | 547,362 | 246,362 | 246,370 | |||
| 560,384 | 560,387 | 575,772 | 575,754 | 565,672 | 565,663 | |||
| 356,475 | 356,486 | 592,277 | 592,268 | 294,277 | 294,289 | |||
| 538,355 | 538,365 | 440,358 | 440,336 | 540,345 | 540,368 | |||
| 550,687 | 550,676 | 568,852 | 568,837 | 568,564 | 568,572 |
*) Для того чтобы оба слагаемых в этом выражении имели одинаковую размерность (в м2), необходимо во втором слагаемом величину разделить на r2 (т.е. выразить в радианной мере).
|
|
|
|
|
|


