 |
Автоматизация решения СЛАУ
|
|
|
|
Постановка задачи
Решить систему линейных алгебраических уравнений 2-мя способами: методом Крамера и методом простой итерации с точностью e=0,01
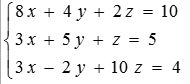
Традиционный способ решения СЛАУ
Решение СЛАУ методом Крамера
1.Запишем исходную матрицу системы.
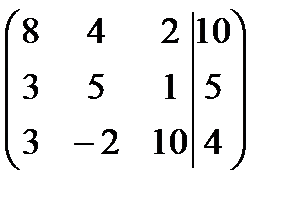
2.Найдем определитель основной матрицы:
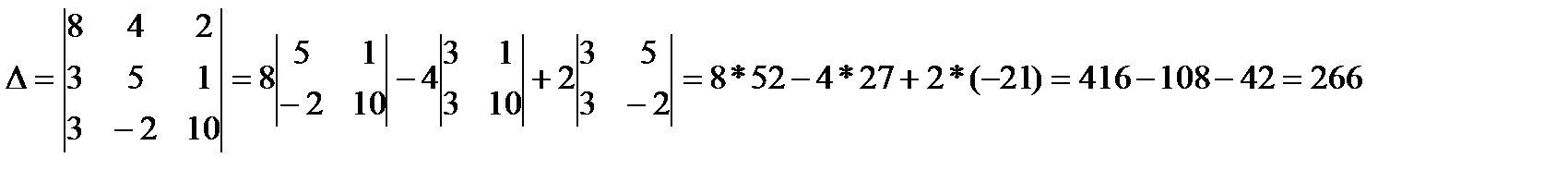 Так как D¹0, то система имеет единственное решение.
Так как D¹0, то система имеет единственное решение.
3.Найдем определители дополнительных матриц, которые получаются из основной путем замены элементов одного из трех столбцов основной матрицы элементами матрицы свободных членов b.
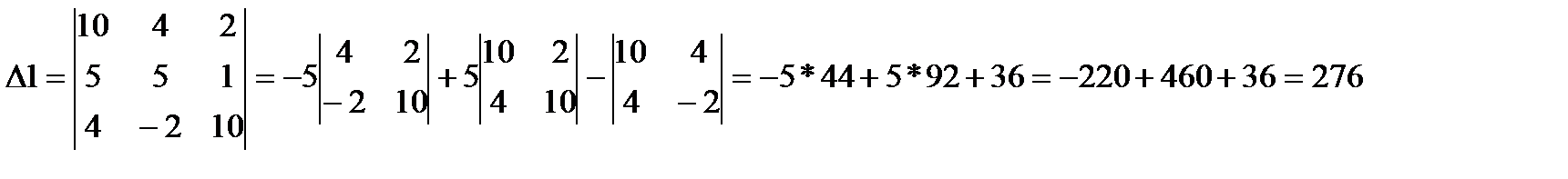
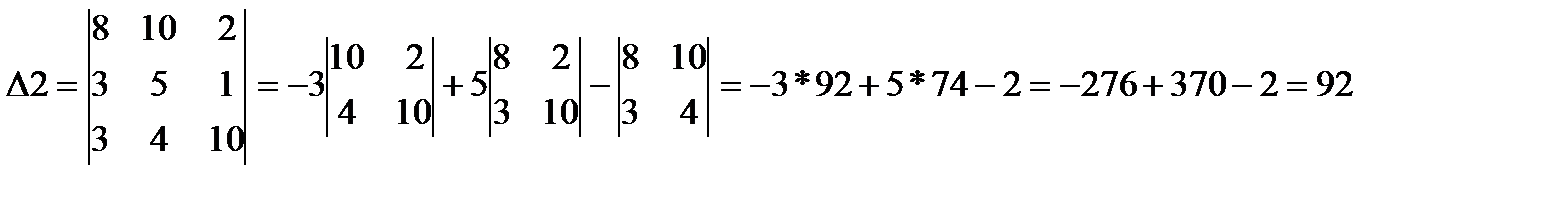
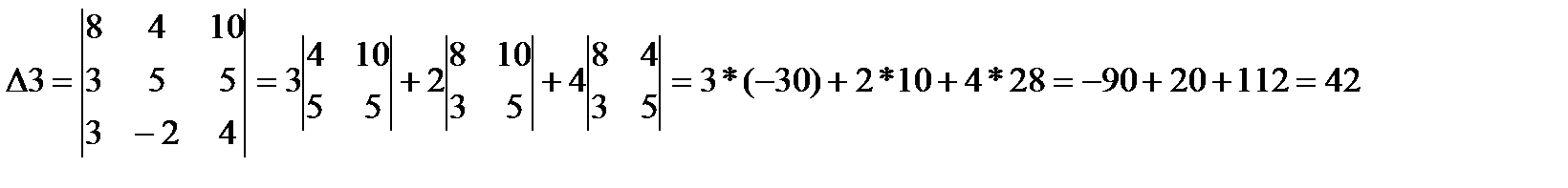
4.Найдем решение системы алгебраических уравнений:
х1=∆1∕∆=276/266=1,04
х2=∆2/∆=92/266=0,35
х3=∆3/∆=42/266=0,16
Решение СЛАУ методом простой итерации
1.Проверяем условия сходимости 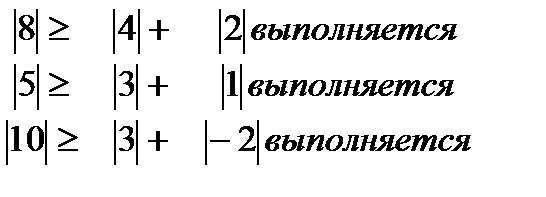
2.Приводим систему к нормальному виду, т.е. из первого уравнения выразим х, из второго у, из третьего z.
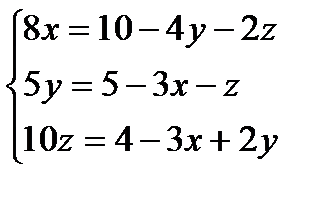
3.Делим первое уравнение на 8,второе - на 5, третье - на 10.
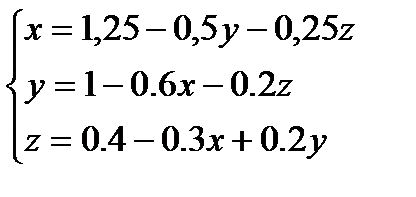
4.Задаем начальное приближение
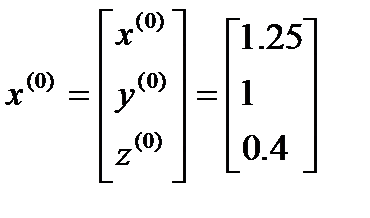
5.Итерационный процесс
Я итерация
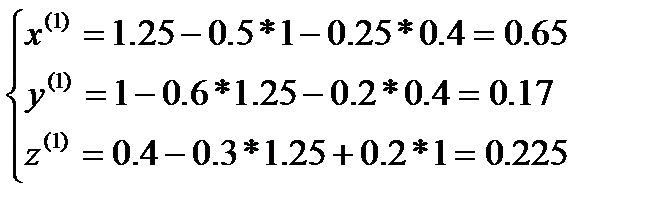
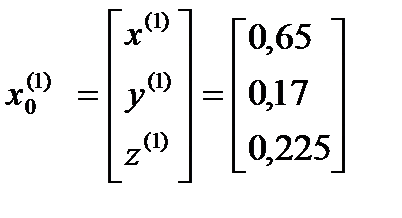
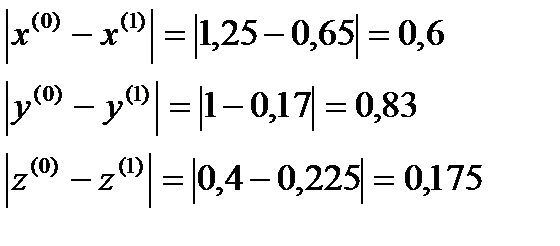
σ=max 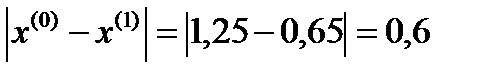 ˃ɛ
˃ɛ
σ=max 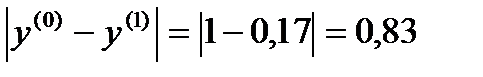 ˃ɛ
˃ɛ
σ=max 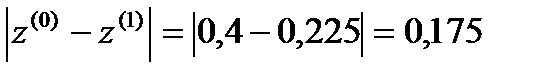 ˃ɛ
˃ɛ
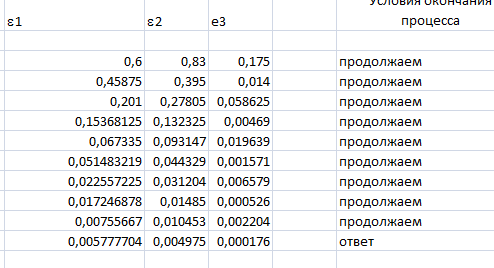
Требуемая точность не достигнута
Я итерация
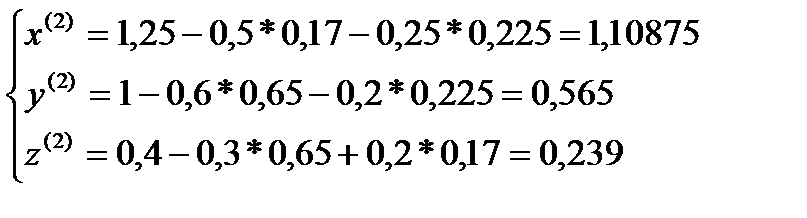
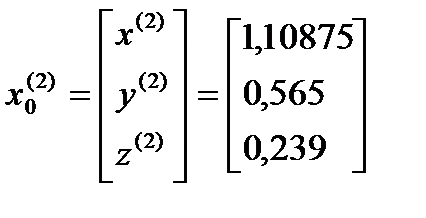
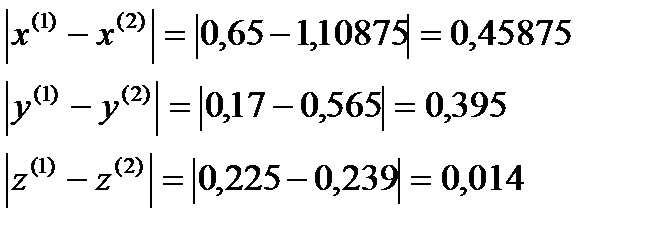
σ=max 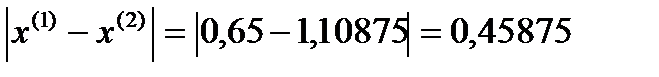 ˃ɛ
˃ɛ
σ=max 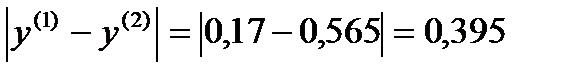 ˃ɛ
˃ɛ
σ=max 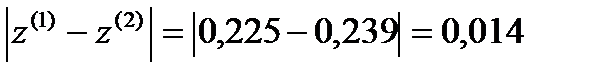 ˃ɛ
˃ɛ
Требуемая точность не достигнута
Я итерация
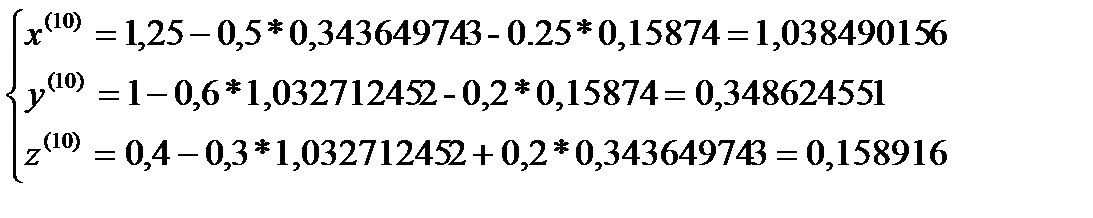
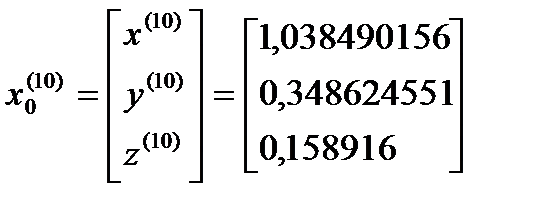
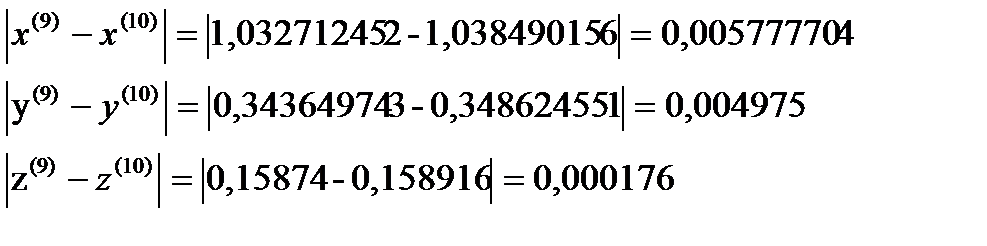
σ=max 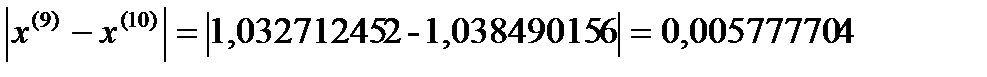 ˂ɛ
˂ɛ
σ=max 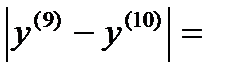
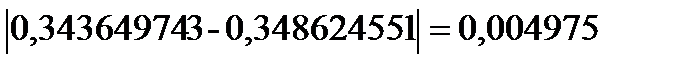 ˂ɛ
˂ɛ
σ=max 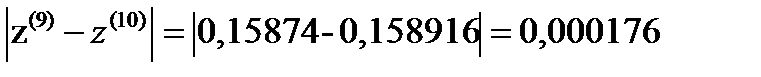 ˂ɛ
˂ɛ
Требуемая точность достигнута
Таким образом,  =
= 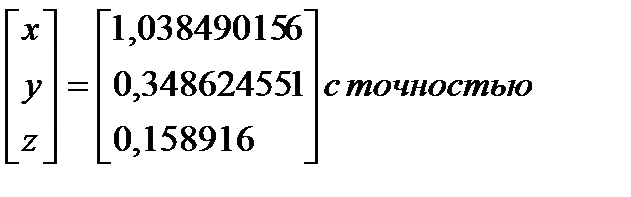 ɛ=0,01
ɛ=0,01
Решение СЛАУ с помощью табличного процессора MS Excel
Решение СЛАУ методом Крамера.
1.Вводим коэффициенты (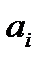 ) и свободные члены системы (
) и свободные члены системы (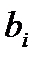 ).
).
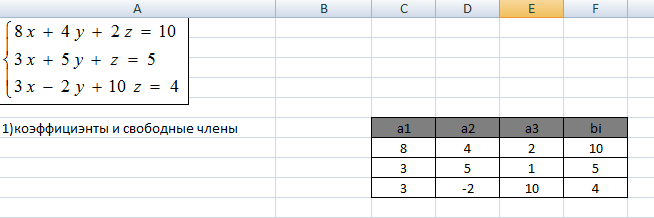
2. С помощью функции ЕСЛИ проанализируем значение определителя основной матрицы. Так как метод Крамера можно использовать для решения систем линейных алгебраических уравнений, у которых определитель основной матрицы не равен 0,то в ячейку D12 вводим формулу =ЕСЛИ(МОПРЕД(C7:E9)<>0;МОПРЕД(C7:E9);"использовать другой метод решения")
|
|
|
Результаты расчета:
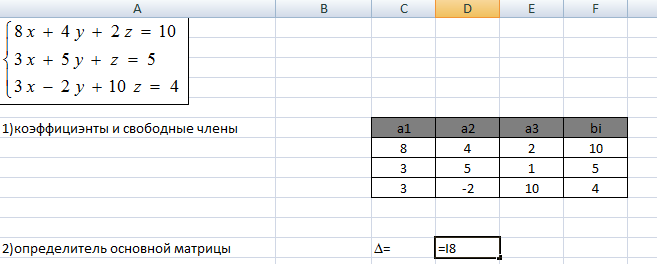
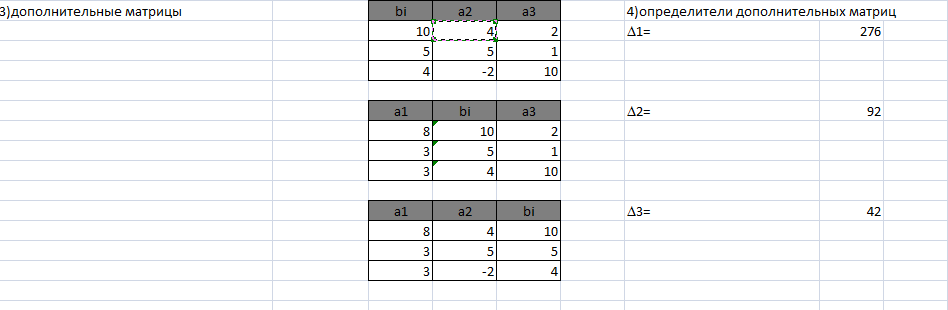
3.Введем дополнительные матрицы системы
Результат:
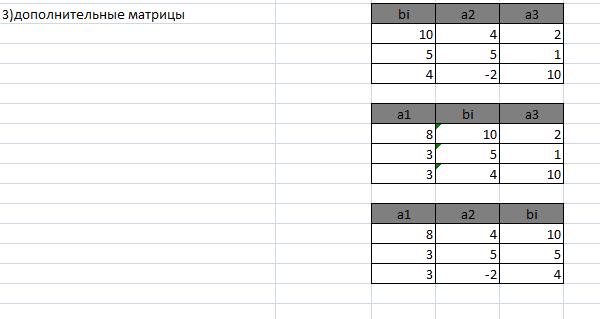
4.Самостоятельно вычислим определители дополнительных матриц системы с помощью функции МОПРЕД():
5.Вычислим решение системы.



Результат вычислений:

6.Проверка


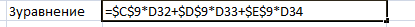
Результат:

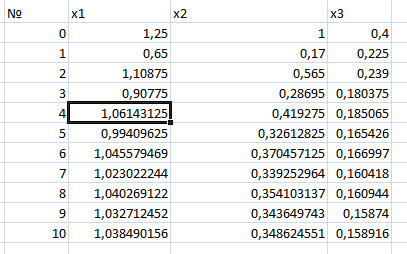
Решение СЛАУ методом простой итерации.
1.Вводим коэффициенты при неизвестных и свободные члены
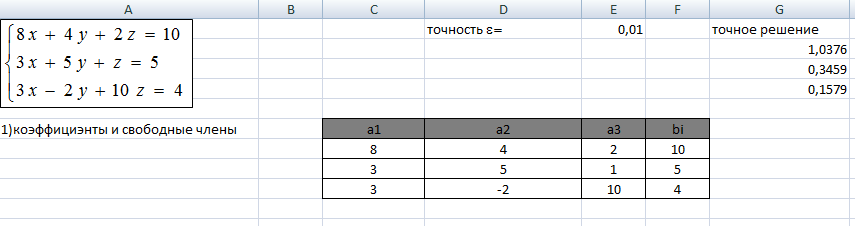
2. Проверяем условие сходимости с помощью функции Если

3. Результат

4.Вводим формулы, вычисляющие начальные приближения к точному значению, итерационные формулы, последовательные приближения к точному значению.
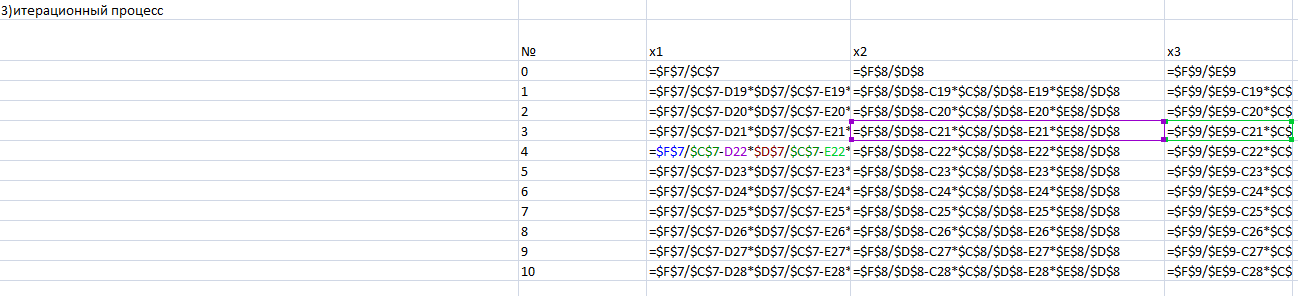
5. Вычислим критерии окончания итерационного процесса

6. Результат
Решение СЛАУ на VBA
Формализация задачи
А)Метод Крамера
B)Метод простой итерации
Входные данные
Вектор свободных членов b={b(i)} – вещественный
Массив коэффициентов при неизвестных a={a(i,j)}-вещественный
Точность вычислений eps-вещественный
Размер системы n-целое
Сумма коэффициентов {a(i,j)} S-вещественная
Критерии окончания итерационного процесса е-вещественный
Максимальный критерий max-вещественный
Выходные данные
Вектор свободных членов b={b(i)} – вещественный
Массив коэффициентов при неизвестных a={a(i,j)}-вещественный
Вектор неизвестных x={x(i)}-вещественные
Математическая модель:
| () |
| () |
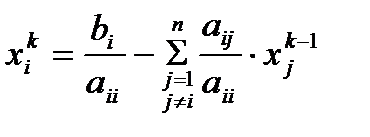
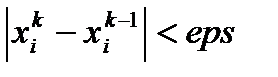
Алгоритмизация
Метод Крамера
| Начало |
| n |
| i=1,n |
| b(i) |
| i=1,n |
| j=1,n |
| a(i,j) |
| i=1,n |
| a(i,j) |
| j=1,n |
| b(i) |
| да |
| Конец |
| x(i) |
| xk=detk/det |
| detk=f(a()) |
| a(i,k)=b(i) |
| a(i,j)=c(I,j) |
| j=1,n |
| i=1,n |
| k=1,n |
| det=0 |
| Вызов функции нахождения det |
| нет |
| да |
| да |
| нет |
| Система не сходится |
| eps=0.01 |
| n |
| i=1,n |
| b(i) |
| i=1,n |
| j=1,n |
| a(i, j) |
| i=1,n |
| b(i) |
| j=1,n |
| a(i, j) |
| i=1,n |
| S=0 |
| j=1,n |
| I ≠ j |
| S=S+|a(I,j)| |
| s>|a(i, j)| |
| 11 |
| 2 |
| Начало |
|
|
|
| max=0 |
| j=1,n |
| bt(i)=b(i)/a(i,j) |
| x(i)=bt(i) |
| xn(i)=bt(i) |
| at(i,j)=0 |
| at(i,j)=-a(i,j)/a(i,j) |
| S=0 |
| S=S+at(i,j)*x(j) |
| x(i)=xn(i) |
| xn(i)=bt(i)+s |
| i=1,n |
| k=0 |
| e=0 |
| i=1,n |
| k=k+1 |
| i=j |
| j=1,n |
| 1 |
| да |
| неть |
| e>max |
| i=1,n |
| x(i)=xn(i) |
| e=|x(i)-xn(i)| |
| max=e |
| max>eps |
| x(i) |
| i=1,n |
| k |
| нет |
| да |
| нет |
| да |
| конец |
|
|
|


