Разложение правильных рациональных дробей с действительными коэффициентами на сумму простейших дробей.

Определение. Дробно-рациональной функцией, или рациональной дробью, называется функция вида:

(1)

где n,mÎN, a₀,a₁,…,a_n,b₀,b₁,…,b_m – постоянные числа. Если n<m, то рациональная дробь (1) называется правильной. Если n³m, то неправильной.

Простейшими рациональными дробями называются дроби следующих типов:

I. 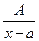; II. , (kÎN, k≥2); III. ; IV.

где a, p, q, А, M, N – постоянные вещественные числа. Имеем

Теорема 1. Пусть имеется правильная рациональная дробь с действительными коэффициентами 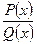. Пусть число аÎR является корнем кратности k знаменателя Q(x), т.е. Q(x)=(x-a)^kφ(x), где φ(а)¹0.

Тогда для дроби 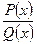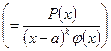справедливо следующее представление:

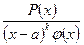= + (2)

где А₁ÎR, Р₁(х) – многочлен с действительными коэффициентами, причем дробь - правильная.

Доказательство. Рассмотрим разность 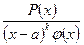R= - или R= .

Р(х)-А₁φ(х) – алгебраический многочлен с действительными коэффициентами.

Для доказательства достаточно подобрать число А₁ таким образом, чтобы многочлен Р(х)-А₁φ(х) делился без остатка на разность (х-а). Это будет лишь тогда, когда число а является корнем многочлена Р(х)-А₁φ(х), т.е. когда Р(а)-А₁φ(а)=0.

Или когда А₁= . Т.к. φ(а)¹0, то такое число А₁ обязательно существует.

Т.о., если в качестве числа А₁ брать число , то будем иметь

Р(х)-А₁φ(х)=(х-а)Р₁(х), где Р₁(х) – алгебраический многочлен с действительными коэффициентами.

Тогда R= 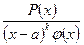- = = т.е.

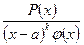= + ч.т.д.

Замечание. Если k>1, то к правильной рациональной дроби так же можно применить теорему 1. В результате получим:

= +

где А₂ÎR, - правильная рациональная дробь с действительными коэффициентами. Продолжая этот процесс, после k-кратного применения теоремы 1, будем иметь:

= + + +…+ + ,

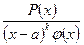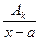где А₁,А₂,А₃,…,А_kÎR (постоянные), а - правильная рациональная дробь с действительными коэффициентами.

Теорема 2. Пусть имеется правильная рациональная дробь с действительными коэффициентами 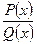. Пусть комплексное число a=a+ib является корнем кратности k знаменателя Q(x) (значит, и число =a-ib также является корнем кратности k знаменателя Q(x)) и, следовательно,

Q(x)=(x-a)^k(x- )^kφ(x)=(x²+px+q)^kφ(x)

где φ(a±ib)¹0. Тогда для дроби 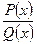(= ) справедливо следующее представление:

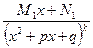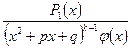= + (3)

где M₁,N₁ÎR, Р₁(х) – многочлен с действительными коэффициентами, причем дробь 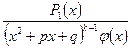- правильная.

Доказательство. Рассмотрим разность R= - 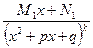или R= .

Р(х)-(M₁x+N₁)φ(х) – алгебраический многочлен с действительными коэффициентами.

Для доказательства достаточно подобрать числа M₁ и N₁ таким образом, чтобы многочлен Р(х)-(M₁x+N₁)φ(х) делился без остатка на (х²+рх+q). Это будет лишь тогда, когда число а=a+ib (значит и число =a-ib) является корнем многочлена Р(х)-(M₁x+N₁)φ(х), т.е. когда

Р(a+ib)-(M₁(a+ib)+N₁)φ(a+ib)=0 (4)

Т.к. φ(a+ib)¹0, то из (4) находим

M₁(a+ib)+N₁= 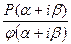Þ(M₁a+N₁)+ibM₁= 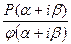Þ

Þ Þ Þ

При таком выборе чисел M₁ и N₁ многочлен Р(х)-(M₁x+N₁)φ(х) делился без остатка на (х-а)(х- )=(х²+рх+q).

Следовательно, будем иметь

Р(х)-(M₁x+N₁)φ(х)=(х²+рх+q)Р₁(х), где Р₁(х) – алгебраический многочлен с действительными коэффициентами.

Тогда R= - 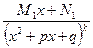= = 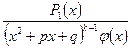т.е.

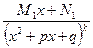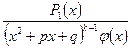= + ч.т.д.

Замечание. Если k>1, то к правильной рациональной дроби 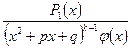так же можно применить теорему 2. В результате получим:

= +

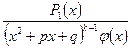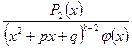
где M₂,N₂ÎR, 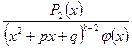- правильная рациональная дробь с действительными коэффициентами. Продолжая этот процесс, после k-кратного применения теоремы 2, будем иметь:

= + +…+ + ,

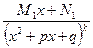где M₁,N₁,M₂,N₂,…,M_k,N_kÎR (постоянные), а - правильная рациональная дробь с действительными коэффициентами.

Следствие из теорем 1 и 2. Пусть 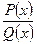- правильная рациональная дробь с действительными коэффициентами. Пусть

Q(x)= ,

a₁,a₂,…,a_r,p₁,q₁,…,p_r,q_r ÎR, , a₁,a₂,…,a_r,b₁,b₂,…,b_sÎN. Тогда справедливо представление:

= + +…+ + + +…+ +…+

+ + +…+ + + +…+ +

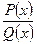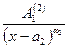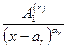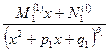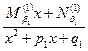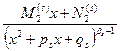+…+ + +…+ (5)

Замечание. Для представления правильной рациональной дроби в виде суммы простейших дробей, выполняют следующие действия:

1) Пишут общий вид представления (5) с буквенными коэффициентами (пока неизвестными).

2) В написанном представлении (5) все дроби приводят к общему знаменателю, которым оказывается Q(x).

3) Т.к. знаменатели получились равными, приравнивают числители правой и левой части равенства (5). Получаем равенство двух многочленов, один из которых имеет конкретные коэффициенты, а другой – неизвестные. Приравнивают коэффициенты при равных степенях х. Получают систему уравнений, из которой находят неизвестные коэффициенты.

Пример.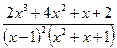

1) Общий вид разложения: = + +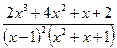

2) Приводим к общему знаменателю:

=

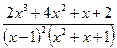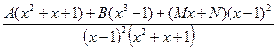
3) Приравниваем коэффициенты при равных степенях:

Получим А=3, В=2, M=0, N=1

Следовательно, = + +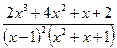

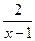⇐ Предыдущая12

Поделиться:

Воспользуйтесь поиском по сайту: