 |
Линеаризация экспоненциальной зависимости.
|
|
|
|
В ряде случаев в качестве эмпирической формулы берут функцию в которую неопределенные коэффициенты входят нелинейно. При этом иногда задачу удается линеаризовать, т.е. свести к линейной. К числу таких зависимостей относится экспоненциальная зависимость
(2.2.1)
где и неопределенные коэффициенты.
Линеаризация достигается путем логарифмирования равенства (2.2.1), после чего получаем соотношение
(2.2.2)
Обозначим и соответственно через и, тогда зависимость (2.2.1) может быть записана в виде, что позволяет применить формулы (2.1.4) с заменой на и на.
Элементы теории корреляции.
График восстановленной функциональной зависимости по результатам измерений называется кривой регрессии. Для проверки согласия построенной кривой регрессии с результатами эксперимента обычно вводят следующие числовые характеристики: коэффициент корреляции (линейная зависимость), корреляционное отношение и коэффициент детерминированности. При этом результаты обычно группируют и представляют в форме корреляционной таблицы. В каждой клетке этой таблицы приводятся численности тех пар, компоненты которых попадают в соответствующие интервалы группировки по каждой переменной. Предполагая длины интервалов группировки (по каждой переменной) равными между собой, выбирают центры (соответственно) этих интервалов и числа в качестве основы для расчетов.
Коэффициент корреляции является мерой линейной связи между зависимыми случайными величинами: он показывает, насколько хорошо в среднем может быть представлена одна из величин в виде линейной функции от другой.
|
|
|
Коэффициент корреляции вычисляется по формуле:
, (2.3.1)
где, и ¾ среднее арифметическое значение соответственно по x и y.
Коэффициент корреляции между случайными величинами по абсолютной величине не превосходит 1. Чем ближе к 1, тем теснее линейная связь между x и y.
В случае нелинейной корреляционной связи условные средние значения располагаются около кривой линии. В этом случае в качестве характеристики силы связи рекомендуется использовать корреляционное отношение, интерпретация которого не зависит от вида исследуемой зависимости.
Корреляционное отношение вычисляется по формуле:
, (2.3.2)
где, а числитель характеризует рассеяние условных средних около безусловного среднего.
Всегда. Равенство соответствует некоррелированным случайным величинам; тогда и только тогда, когда имеется точная функциональная связь между y и x. В случае линейной зависимости y от x корреляционное отношение совпадает с квадратом коэффициента корреляции. Величина используется в качестве индикатора отклонения регрессии от линейной.
Корреляционное отношение является мерой корреляционной связи y с x в какой угодно форме, но не может дать представления о степени приближенности эмпирических данных к специальной форме. Чтобы выяснить насколько точно построенная кривая отражает эмпирические данные вводится еще одна характеристика ¾ коэффициент детерминированности.
Для его описания рассмотрим следующие величины. - полная сумма квадратов, где среднее значение.
Можно доказать следующее равенство
.
Первое слагаемое равно и называется остаточной суммой квадратов. Оно характеризует отклонение экспериментальных данных от теоретических.
Второе слагаемое равно и называется регрессионной суммой квадратов и оно характеризует разброс данных.
|
|
|
Очевидно, что справедливо следующее равенство.
Коэффициент детерминированности определяется по формуле:
. (2.3.3)
Чем меньше остаточная сумма квадратов по сравнению с общей суммой квадратов, тем больше значение коэффициента детерминированности, который показывает, насколько хорошо уравнение, полученное с помощью регрессионного анализа, объясняет взаимосвязи между переменными. Если он равен 1, то имеет место полная корреляция с моделью, т.е. нет различия между фактическим и оценочным значениями y. В противоположном случае, если коэффициент детерминированности равен 0, то уравнение регрессии неудачно для предсказания значений y.
Коэффициент детерминированности всегда не превосходит корреляционное отношение. В случае когда выполняется равенство то можно считать, что построенная эмпирическая формула наиболее точно отражает эмпирические данные.
Расчет коэффициентов аппроксимации в Microsoft Excel.
Вариант №22
Функция y=f(x) задана таблицей 1
Таблица 1
Исходные данные.
| 12.85 | 154.77 | 9.65 | 81.43 | 7.74 | 55.86 | 5.02 | 24.98 | 1.86 | 3.91 |
| 12.32 | 145.59 | 9.63 | 80.97 | 7.32 | 47.63 | 4.65 | 22.87 | 1.76 | 3.22 |
| 11.43 | 108.37 | 9.22 | 79.04 | 7.08 | 48.03 | 4.53 | 20.32 | 1.11 | 1.22 |
| 10.59 | 100.76 | 8.44 | 61.76 | 6.87 | 36.85 | 3.24 | 9.06 | 0.99 | 1.10 |
| 10.21 | 98.32 | 8.07 | 60.54 | 5.23 | 25.65 | 2.55 | 6.23 | 0.72 | 0.53 |
Требуется выяснить - какая из функций - линейная, квадратичная или экспоненциальная наилучшим образом аппроксимирует функцию заданную таблицей 1.
Решение.
Поскольку в данном примере каждая пара значений встречается один раз, то между и существует функциональная зависимость.
Для проведения расчетов данные целесообразно расположить в виде таблицы 2, используя средства табличного процессора Microsoft Excel.
Таблица 2

Расчет сумм.
Поясним как таблица 2 составляется.
Шаг 1. В ячейки A2:A26 заносим значения.
Шаг 2. В ячейки B2:B26 заносим значения.
Шаг 3. В ячейку C2 вводим формулу =A2^2.
Шаг 4. В ячейки C3:C26 эта формула копируется.
Шаг 5. В ячейку D2 вводим формулу =A2*B2.
Шаг 6. В ячейки D3:D26 эта формула копируется.
Шаг 7. В ячейку F2 вводим формулу =A2^4.
Шаг 8. В ячейки F3:F26 эта формула копируется.
Шаг 9. В ячейку G2 вводим формулу =A2^2*B2.
|
|
|
Шаг 10. В ячейки G3:G26 эта формула копируется.
Шаг 11. В ячейку H2 вводим формулу =LN(B2).
Шаг 12. В ячейки H3:H26 эта формула копируется.
Шаг 13. В ячейку I2 вводим формулу =A2*LN(B2).
Шаг 14. В ячейки I3:I26 эта формула копируется.
Последующие шаги делаем с помощью автосуммирования.
Шаг 15. В ячейку A27 вводим формулу =СУММ(A2:A26).
Шаг 16. В ячейку B27 вводим формулу =СУММ(B2:B26).
Шаг 17. В ячейку C27 вводим формулу =СУММ(C2:C26).
Шаг 18. В ячейку D27 вводим формулу =СУММ(D2:D26).
Шаг 19. В ячейку E27 вводим формулу =СУММ(E2:E26).
Шаг 20. В ячейку F27 вводим формулу =СУММ(F2:F26).
Шаг 21. В ячейку G27 вводим формулу =СУММ(G2:G26).
Шаг 22. В ячейку H27 вводим формулу =СУММ(H2:H26).
Шаг 23. В ячейку I27 вводим формулу =СУММ(I2:I26).
Аппроксимируем функцию линейной функцией. Для определения коэффициентов и воспользуемся системой
Используя итоговые суммы таблицы 2, расположенные в ячейках A27, B27, C27 и D27, запишем систему в виде

решив которую, получим  и
и 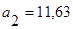 .
.
Таким образом, линейная аппроксимация имеет вид  .
.
Решение системы проводили, пользуясь средствами Microsoft Excel. Результаты представлены в таблице 3.
 |
Таблица 3
|
|
|


