Вопрос№12 Расстояние между параллельными плоскостями.

Рассмотрим две параллельные плоскости и . Возьмем на любой из этих плоскостей точку М₁ и опустим перпендикуляр М₁H₁ из этой точки на другую плоскость. Длина перпендикуляра M₁H₁ является расстоянием между параллельными плоскостями и .

Определение.

Расстояние между параллельными плоскостями – это расстояние от произвольной точки одной из параллельных плоскостей до другой плоскости.

чтобы найти расстояние между двумя параллельными плоскостями нужно:

• определить координаты точки М₁, лежащей в одной из заданных плоскостей;
• найти нормальное уравнение другой плоскости в виде ;
• вычислить искомое расстояние по формуле .

асстояние между параллельными плоскостями и вычисляется по формуле .

Вопрос№13 расстояние от точки до плоскости.

Расстояние от точки до плоскости — равно длине перпендикуляра, опущенного из точки на плоскость.

Формула для вычисления расстояния от точки до плоскости

Если задано уравнение плоскости Ax + By + Cz + D = 0, то расстояние от точки M(M_x, M_y, M_z) до плоскости можно найти, используя следующую формулу:

 

d =	|A·Mx + B·My + C·Mz + D|
√A2 + B2 + C2

Вопрос№14 угол между плоскостями

Двугранный угол между плоскостями равен углу образованному нормальными векторами этих плоскостей.

Определение.

Двугранный угол между плоскостями равен углу образованному прямыми l₁ и l₂, лежащими в соответствующих плоскостях и перпендикулярными линии пересечения плоскостей.

Формула для вычисления угла между плоскостями

Если заданы уравнения плоскостей A₁x + B₁y + C₁z + D₁ = 0 и A₂x + B₂y + C₂z + D₂ = 0, то угол между плоскостями можно найти, используя следующую формулу

cos α =	|A1·A2 + B1·B2 + C1·C2|
√A12 + B12 + C12√A22 + B22 + C22

 

Вопрос№15 Уравнения прямой в пространстве (канонические, параметрические). Уравнение прямой проходящей через 2 данные точки

Параметрические уравнения прямой в пространстве имеют вид , где x₁, y₁ и z₁ – координаты некоторой точки прямой, a_x, a_y и a_z (a_x, a_y и a_z одновременно не равны нулю) - соответствующие координаты направляющего вектора прямой, а 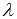- некоторый параметр, который может принимать любые действительные значения.

При любом значении параметра 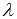по параметрическим уравнениям прямой в пространстве мы можем вычислить тройку чисел , она будет соответствовать некоторой точке прямой (отсюда и название этого вида уравнений прямой). К примеру, при из параметрических уравнений прямой в пространстве получаем координаты x₁, y₁ и z₁:

Разрешив каждое из параметрических уравнений прямой вида относительно параметра 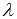, легко перейти к каноническим уравнениям прямой в пространстве вида .

Канонические уравнения прямой в пространстве определяют прямую, проходящую через точку , а направляющим вектором прямой является вектор. Следует отметить, что одно или два из чисел в канонических уравнениях прямой могут быть равны нулю (все три числа одновременно не могут быть равны нулю, так как направляющий вектор прямой не может быть нулевым). Тогда запись вида считается формальной (так как в знаменателях одной или двух дробей будут нули) и ее следует понимать как , где .

Если одно из чисел в канонических уравнениях прямой равно нулю, то прямая лежит в одной из координатных плоскостей, либо в плоскости ей параллельной. Если два из чисел равны нулю, то прямая либо совпадает с одной из координатных осей, либо параллельна ей.

Если известны две точки пространства , то уравнения прямой, проходящей через данные точки, выражаются формулами:

Унылый частный случай предыдущего параграфа. И в самом деле, вектор является направляющим вектором прямой.

⇐ Предыдущая123Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: