 |
Вопрос№17 Угол между прямой и плоскостью в пространстве.
|
|
|
|
⇐ ПредыдущаяСтр 3 из 3
Если в пространстве заданы направляющий вектор прямой L
s = {l; m; n}
и уравнение плоскости
Ax + By + Cz + D = 0,
то угол между этой прямой и плоскостью можно найти используя формулу
| sin φ = | | A · l + B · m + C · n | |
| √A2 + B2 + C2 · √l2 + m2 + n2 |
Вывод формулы для вычисления угла между прямой и плоскостью
Из уравнения прямой можно найти направляющий вектор прямой
s = {l; m; n}
Из уравнения плоскости вектор нормали плоскости имеет вид
q = {A; B; C}
Из формул скалярного произведения векторов найдем косинус угла между нормалью к плоскости и направляющим вектором прямой
| cos ψ = | | q · s | |
| | s | · |q | |
Так как φ = 90° - ψ, то синус угла между прямой и плоскостью sin φ = cos ψ.
Расписав скалярное произведение векторов и модуль векторов через их координаты, получим формулу для вычисления угла между прямой и плоскостью.
 Числа
Числа  называются членами последовательности, а число
называются членами последовательности, а число  – общим или n-ным членом данной последовательности. Например: 2, 4, 6, 8, …, 2n.
Число
– общим или n-ным членом данной последовательности. Например: 2, 4, 6, 8, …, 2n.
Число  называется пределом последовательности
называется пределом последовательности  , если для любого
, если для любого  существует номер
существует номер  , зависящий от
, зависящий от  такой, что для любого
такой, что для любого  выполняется неравенство
выполняется неравенство  .
.
 Последовательность
Последовательность  называется ограниченной сверху, если существует такое число M>0, что для любого номера
называется ограниченной сверху, если существует такое число M>0, что для любого номера  ,
,  Монотонные последовательности: Последовательность
Монотонные последовательности: Последовательность  называется неубывающей, если каждый элемент этой последовательности не превосходит следующего за ним.
называется неубывающей, если каждый элемент этой последовательности не превосходит следующего за ним.
 — неубывающая
— неубывающая  Последовательность
Последовательность  называется невозрастающей, если каждый следующий элемент этой последовательности не превосходит предыдущего.
называется невозрастающей, если каждый следующий элемент этой последовательности не превосходит предыдущего.
 — невозрастающая
— невозрастающая  Теорема. Всякая монотонная ограниченная последовательность имеет предел (М).
Последовательность
Теорема. Всякая монотонная ограниченная последовательность имеет предел (М).
Последовательность  называется бесконечно малой, если
называется бесконечно малой, если  , т.е.
, т.е.  . Пример:
. Пример:  Последовательность
Последовательность  называется бесконечно большой, если
называется бесконечно большой, если  , или
, или 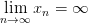 . Пример:
. Пример:  2.Определение предела функции, определения односторонних пределов. Необходимое и достаточное условие существования предела функции в точке (сформулировать).
1) Определение предела ф-ции в точке Число А называется пределом ф-ции f(x) в точке x=a (
2.Определение предела функции, определения односторонних пределов. Необходимое и достаточное условие существования предела функции в точке (сформулировать).
1) Определение предела ф-ции в точке Число А называется пределом ф-ции f(x) в точке x=a ( ) ó
) ó  : ∀х ∈ Ủ (a, δ) =>
: ∀х ∈ Ủ (a, δ) =>  Замечание. Ủ- проколотой δ-окрестностью точки а называется следующее множество: Ủ(a, δ) = (а – δ; а)∪(а; а + δ)
Из определения пределов ф-ции следует, что чем ближе значение х к точке а, тем меньше различаются значение ф-ции и значение предела А.
2) Определение пределов ф-ции на +∞
Замечание. Ủ- проколотой δ-окрестностью точки а называется следующее множество: Ủ(a, δ) = (а – δ; а)∪(а; а + δ)
Из определения пределов ф-ции следует, что чем ближе значение х к точке а, тем меньше различаются значение ф-ции и значение предела А.
2) Определение пределов ф-ции на +∞

 Из определения следует, что чем больше значение х, тем меньше различаются значение ф-ции и значение предела А.
3) Определение пределов ф-ции на
Из определения следует, что чем больше значение х, тем меньше различаются значение ф-ции и значение предела А.
3) Определение пределов ф-ции на  ∞
Число А называется пределом ф-цииf(x) при х, стремящемся к минус бесконечности
∞
Число А называется пределом ф-цииf(x) при х, стремящемся к минус бесконечности  ó
ó  :
:  х<S =>
х<S =>  Из определения следует, что чем меньше значение х, тем меньше различаются значение ф-ции и значение предела А.
Определение односторонних примеров. Пределом слева ф-ции f(x) в точке х=а называется число А (
Из определения следует, что чем меньше значение х, тем меньше различаются значение ф-ции и значение предела А.
Определение односторонних примеров. Пределом слева ф-ции f(x) в точке х=а называется число А (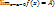 ó
ó  : ∀х ∈ (a- δ; a) =>
: ∀х ∈ (a- δ; a) =>  Иначе можно обозначить предел слева f(a-0).
Пределом справа ф-ции f(x) в точке х=а называется число В
(
Иначе можно обозначить предел слева f(a-0).
Пределом справа ф-ции f(x) в точке х=а называется число В
( ó
ó  : ∀х ∈ (а; а+ δ) =>
: ∀х ∈ (а; а+ δ) =>  Иначе можно обозначить f(a+0).
Теорема. Необходимое и достаточное условие существования пределов ф-ции в точке. Для того, чтобы в точке х=
Иначе можно обозначить f(a+0).
Теорема. Необходимое и достаточное условие существования пределов ф-ции в точке. Для того, чтобы в точке х=  существовал предел, необходимо и достаточно существование обоих односторонних пределов, равных между собой
существовал предел, необходимо и достаточно существование обоих односторонних пределов, равных между собой  3.Теорема о единственности предела. Теоремы о свойствах ф-ций, имеющих предел. Теорема. Если функция
3.Теорема о единственности предела. Теоремы о свойствах ф-ций, имеющих предел. Теорема. Если функция 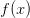 в точке
в точке  имеет предел, то этот предел единственный. Докажем методом от противного. Предположим, что
имеет предел, то этот предел единственный. Докажем методом от противного. Предположим, что  ,
,  ,
,  . Возьмём
. Возьмём  , по определению и свойству окрестности найдётся такая проколотая
, по определению и свойству окрестности найдётся такая проколотая  -окрестность точки
-окрестность точки  (
( ), в которой одновременно будут выполнятся неравенства
), в которой одновременно будут выполнятся неравенства  ,
,  , тогда в точках этой же окрестности
, тогда в точках этой же окрестности 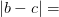

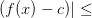
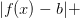


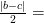
 Получили противоречие
Получили противоречие 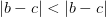 . Отсюда, функция
. Отсюда, функция 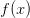 в точке
в точке  имеет единственный предел.
Основные теоремы о пределе ф-ций. 1) Пусть ф-ция y=f(x) определена в некоторой окрестности точки х=а и принимает в этой окрестности постоянное значение f(x)=C, тогда предел ф-ции также равен С:
имеет единственный предел.
Основные теоремы о пределе ф-ций. 1) Пусть ф-ция y=f(x) определена в некоторой окрестности точки х=а и принимает в этой окрестности постоянное значение f(x)=C, тогда предел ф-ции также равен С:  2) Пусть ф-ция y=f(x) определена в некоторой окрестности точки х=а и для всех Х в этой окрестности выполняется неравенство f(x)>p (или f(x)<p) Тогда, если в точке а существует предел, то он ≥p (или ≤p). Следствие: если в некоторой окрестности точки х=а ф-ция положительна, то пределом, если он есть, будет число неотрицательное (≥0). А если ф-ция отрицательная, то предел неположительный (≤0).
3) Пусть ф-ция y=f(x) определена в некоторой окрестности точки х=а и существует
2) Пусть ф-ция y=f(x) определена в некоторой окрестности точки х=а и для всех Х в этой окрестности выполняется неравенство f(x)>p (или f(x)<p) Тогда, если в точке а существует предел, то он ≥p (или ≤p). Следствие: если в некоторой окрестности точки х=а ф-ция положительна, то пределом, если он есть, будет число неотрицательное (≥0). А если ф-ция отрицательная, то предел неположительный (≤0).
3) Пусть ф-ция y=f(x) определена в некоторой окрестности точки х=а и существует  a. Тогда, если M≤A≤N, то существует окрестность, для которой M≤f(x)≤N. Следствие: если ф-ция имеет предел, то она ограниченна в некоторой окрестности точки.
4) Теорема о пределе промежуточной ф-ции. Пусть ф-ции y=f(x), y=φ(x), y=ψ(x) определены в некоторой окрестности точки х=а и пусть для всех х из этой окрестности выполняется: φ(x) ≤ f(x) ≤ ψ(x). Тогда, если существуют пределы
a. Тогда, если M≤A≤N, то существует окрестность, для которой M≤f(x)≤N. Следствие: если ф-ция имеет предел, то она ограниченна в некоторой окрестности точки.
4) Теорема о пределе промежуточной ф-ции. Пусть ф-ции y=f(x), y=φ(x), y=ψ(x) определены в некоторой окрестности точки х=а и пусть для всех х из этой окрестности выполняется: φ(x) ≤ f(x) ≤ ψ(x). Тогда, если существуют пределы  =А, тогда существует и предел
=А, тогда существует и предел  =А. Доказательство. Из определения 1 предела ф-ции в точке следует:
=А. Доказательство. Из определения 1 предела ф-ции в точке следует:  =А ó
=А ó  Ủ(a;
Ủ(a;  ) => |
) => |  -A|<
-A|<  Для другой ф-ции:
Для другой ф-ции:  =А ó
=А ó  Ủ(a;
Ủ(a;  ) => | ψ(x) -A|<
) => | ψ(x) -A|<  Рассмотрим неравенство из условия: φ(x) ≤ f(x) ≤ ψ(x). Тогда: |f(x) – A| ≤ max
Рассмотрим неравенство из условия: φ(x) ≤ f(x) ≤ ψ(x). Тогда: |f(x) – A| ≤ max 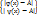 ≤
≤  , если взять значения х из интервала Ủ(а;
, если взять значения х из интервала Ủ(а;  ), где
), где  . Это и означает существование пределов ф-ций f(x) в точке х=а.
4.Бесконечно малые и бесконечно большие функции (определения). Теорема о связи б.м. и б.б. функций. Функция y=f(x) называется бесконечно малой при x→a или при x →∞, если
. Это и означает существование пределов ф-ций f(x) в точке х=а.
4.Бесконечно малые и бесконечно большие функции (определения). Теорема о связи б.м. и б.б. функций. Функция y=f(x) называется бесконечно малой при x→a или при x →∞, если  или
или 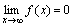 , т.е. бесконечно малая функция – это функция, предел которой в данной точке равен нулю. Функция
, т.е. бесконечно малая функция – это функция, предел которой в данной точке равен нулю. Функция 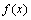 называется бесконечно большой при
называется бесконечно большой при  , если
, если  .
Теорема. Теорема о представлении ф-ции. Пусть ф-ция y=f(x) определена в некоторой окрестности точки х=а
.
Теорема. Теорема о представлении ф-ции. Пусть ф-ция y=f(x) определена в некоторой окрестности точки х=а  ó
ó  , где
, где 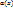 - б.м.ф. при х
- б.м.ф. при х  а Доказательство. По определению предела ф-ции
а Доказательство. По определению предела ф-ции  ó
ó  Ủ(a;
Ủ(a;  => |f(x) – A|<
=> |f(x) – A|<  (f(x) – A=
(f(x) – A= 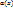 ) ó
) ó  Ủ(a;
Ủ(a;  => |
=> | 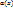 -0|<
-0|<  ó
ó 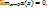 следовательно
следовательно 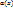 - б.м.ф. при
- б.м.ф. при  и
и  Это равносильно
Это равносильно  , где
, где 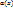 - б.м.ф. при
- б.м.ф. при  . Замечание. Теорема позволяет доказывать утверждение, не прибегая к определению предела.
Теорема. Связь между б.м. и б.б. функциями.
. Замечание. Теорема позволяет доказывать утверждение, не прибегая к определению предела.
Теорема. Связь между б.м. и б.б. функциями.  5. Свойства б.м.ф. (без доказательств). Сравнение б.м.ф.; эквивалентные функции.
Основные свойства б.м.ф. 1) Сумма конечного числа б.м.ф. при
5. Свойства б.м.ф. (без доказательств). Сравнение б.м.ф.; эквивалентные функции.
Основные свойства б.м.ф. 1) Сумма конечного числа б.м.ф. при  есть б.м.ф.при
есть б.м.ф.при  б.м.
б.м.  +
+ 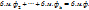 2) Произведение ограниченной функции на б.м.ф. при
2) Произведение ограниченной функции на б.м.ф. при  есть б.м.ф. при
есть б.м.ф. при  огр.пос-ность * б.м.п. = б.м.п. 3)Произведение конечного числа б.м.ф. при
огр.пос-ность * б.м.п. = б.м.п. 3)Произведение конечного числа б.м.ф. при  есть б.м.ф. при
есть б.м.ф. при 
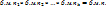 Сравнение б.м.ф. Пусть
Сравнение б.м.ф. Пусть 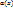 и
и  – б.м.ф. при
– б.м.ф. при  и пусть существует
и пусть существует  , тогда: 1) при А=0,
, тогда: 1) при А=0, 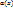 называется б.м.ф. более высокого порядка, чем
называется б.м.ф. более высокого порядка, чем  2) при А=∞,
2) при А=∞, 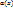 называется б.м.ф. более низкого порядка, чем
называется б.м.ф. более низкого порядка, чем  3) при А=1,
3) при А=1, 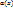 и
и  называются эквивалентными б.м. Обозначается
называются эквивалентными б.м. Обозначается  при
при  4) при А=const, А
4) при А=const, А  ,
, 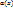 и
и  называются б.м. одного порядка 5) если предел не существует, то
называются б.м. одного порядка 5) если предел не существует, то 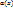 и
и  называются несравнимыми б.м.
Таблица эквивалентности функций (
называются несравнимыми б.м.
Таблица эквивалентности функций ( )
)  й
Теорема. Пусть
й
Теорема. Пусть  - б.м.ф. при
- б.м.ф. при 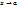 ; и пусть
; и пусть 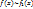 и
и 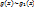 при
при 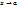 , тогда
, тогда  6. Основные свойства пределов (арифметические) Теорема. Арифметические свойства пределов.
Пусть функции f(x) и g(x) определены в некоторой окрестности точки х=
6. Основные свойства пределов (арифметические) Теорема. Арифметические свойства пределов.
Пусть функции f(x) и g(x) определены в некоторой окрестности точки х=  и пусть существует
и пусть существует  и
и 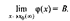 1)
1)  2)
2) 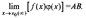 3)
3)  Доказательство. Из теоремы о представлении функций следует, что
Доказательство. Из теоремы о представлении функций следует, что  б.м.ф.;
б.м.ф.; 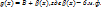 ; 𝑓
; 𝑓  ,
,  Следовательно по теореме о представлении функций
Следовательно по теореме о представлении функций  . Остальные пункты аналогичны.
7. 1-й и 2-й замечательные пределы. Примеры их применения.
1-й замечательный предел.
. Остальные пункты аналогичны.
7. 1-й и 2-й замечательные пределы. Примеры их применения.
1-й замечательный предел. 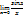 Замечания: 1) 1-й замечательный предел раскрывает неопределенность вида
Замечания: 1) 1-й замечательный предел раскрывает неопределенность вида  ; 2) На практике удобнее этот предел применять в виде
; 2) На практике удобнее этот предел применять в виде  Например.
2-й замечательный предел.
Например.
2-й замечательный предел.  Замечания: 1) Второй замечательный предел раскрывает неопределенность вида
Замечания: 1) Второй замечательный предел раскрывает неопределенность вида  ; 2) На практике удобнее представлять этот предел в виде
; 2) На практике удобнее представлять этот предел в виде  Например.
8. Непрерывность функции в точке. Классификация точек разрыва.
Пусть функция y=f(x) определена в некоторой окрестности точки
Например.
8. Непрерывность функции в точке. Классификация точек разрыва.
Пусть функция y=f(x) определена в некоторой окрестности точки  . Функция называется непрерывной в точке
. Функция называется непрерывной в точке  , если выполнены следующие условия: 1) функция определена в точке
, если выполнены следующие условия: 1) функция определена в точке  т.е.
т.е.  ; 2)
; 2)  ; 3)
; 3)  . Использую данное определение непрерывности, можно вывести другое определение: рассмотрим 3 пункт определения и учтем теорему о представлении функции
. Использую данное определение непрерывности, можно вывести другое определение: рассмотрим 3 пункт определения и учтем теорему о представлении функции  ó
ó  ó
ó  при
при 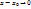
 ó
ó  – второе определение непрерывности функции в точке.
Если нарушено хотя бы одно условие первого определения непрерывности функции в точке, то
– второе определение непрерывности функции в точке.
Если нарушено хотя бы одно условие первого определения непрерывности функции в точке, то  называется точкой разрыва.
Если в точке
называется точкой разрыва.
Если в точке  существуют оба односторонних предела (конечных числовых), то
существуют оба односторонних предела (конечных числовых), то  называется точкой разрыва 1 рода. 1) Точка разрыва 1 рода – «скачок»
называется точкой разрыва 1 рода. 1) Точка разрыва 1 рода – «скачок» 
 2) Точка разрыва 1 рода – «устранимая»
2) Точка разрыва 1 рода – «устранимая» 
 Точки разрыва, не являющиеся точками разрыва 1 рода, являются точками разрыва 2 рода (если хотя бы один предел не существует или равен бесконечности).
9.Свойства функция, непрерывных на отрезке (сформулировать).
Если функция f(x) непрерывна в каждой точке х
Точки разрыва, не являющиеся точками разрыва 1 рода, являются точками разрыва 2 рода (если хотя бы один предел не существует или равен бесконечности).
9.Свойства функция, непрерывных на отрезке (сформулировать).
Если функция f(x) непрерывна в каждой точке х  М, то ее называют непрерывной на множестве М.
Функция y=f(x) называется непрерывной на отрезке
М, то ее называют непрерывной на множестве М.
Функция y=f(x) называется непрерывной на отрезке 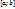 , если выполнены следующие условия: 1) она непрерывна в каждой точке х из интервала (а; b); 2)
, если выполнены следующие условия: 1) она непрерывна в каждой точке х из интервала (а; b); 2)  ;
;  .
Теорема. Свойства функций, непрерывных на отрезке. Пусть y=f(x) определена и непрерывна на отрезке
.
Теорема. Свойства функций, непрерывных на отрезке. Пусть y=f(x) определена и непрерывна на отрезке 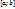 , тогда: 1) она достигает на этом отрезке свои наибольшее и наименьшее значения; 2) если на концах отрезка функция принимает значения разных знаков, то найдется хотя бы одна такая точка х=с
, тогда: 1) она достигает на этом отрезке свои наибольшее и наименьшее значения; 2) если на концах отрезка функция принимает значения разных знаков, то найдется хотя бы одна такая точка х=с  (a; b), для которой f(c)=0; 3) если на концах отрезка функция принимает неравные между собой значения А и В (A<B), то она принимает и любое промежуточное значение С
(a; b), для которой f(c)=0; 3) если на концах отрезка функция принимает неравные между собой значения А и В (A<B), то она принимает и любое промежуточное значение С  (А; В) в некоторой точке х=с
(А; В) в некоторой точке х=с  (а; b).
Теорема. Пусть функции y=f(x) и y=g(x) непрерывны на некотором множестве М, тогда непрерывными будут и следующие функции: 1)
(а; b).
Теорема. Пусть функции y=f(x) и y=g(x) непрерывны на некотором множестве М, тогда непрерывными будут и следующие функции: 1) 
 3)
3)  , при g(x)
, при g(x)  0 для всех х
0 для всех х  М.
М.
 производная сложной функции.пусть функция у=у(х) диффернц. на множестве х,а функция х=х(t) диффернц на множестве Т,тогда для вычисления производной сложной функции y=(y(x(t)) – y(x(t)))’=y’x*x’t
производная параметрически заданной функции.Пусть функц. задана в параллели виде у=у(t) х=х(t),где х(t) и y(t) дифференцфункц. параметра t.тогда производная y’(t) находят по формуле Y’x=y’(t):x’(t)
5)Производная показательно-степенной функции.
функция вида у=И(х)^t(x) показательно степенная.длядиффернцирования нельзя применять ни формулы для показательной функции ни формулу для степенной.
lny=lnИ(X)^t(x)
lny=t(x) * lnИ(x) невно заданная
1/у *у’=И’(x) *lnИ(x) +t(x) * 1/И(х) * И’(x)
умножим обе части на у=И(х)^t(x)
y’=(И’(x) *lnИ(x)* И(х)^t(x)+ 1/И(х) * И’(x)* И(х)^t(x)
6. Теорема Ферма. Теорема Ролля. Теорема Лагранжа. Теорема Коши (сформулировать).
ТЕОРМЕРА ФЕРМА
Пусть функция y=f(x) определена и непрерывна на отрезке [a;b]. Если в некоторой очке х=с∈ (а;b) функция достигает своего наибольшего или наименьшего значения,то если производная в этой точке существует, она равно 0⇒f*(c)=0
ТЕОРЕМА РОЛЛЯ
Пусть функция y=f(x) определена на отрезке [a;b]. если функция удовлетворяет условия
1. непрерывна на [a;b]
2. дифференцируема на (a;b)
3. f(a)=f(b)
Если выполнено условие, то найдется хотя бы 1 такая точка x=c∈ (a;b) для которой справедливо f*(c)=0
ТЕОРЕМА ЛАНГРАДЖА
Пусть функция y=f(x) определена на [a;b]. Если функция отвечает условиям:
1)непрерывна на [a;b]
2. дифференцируемана (a;b)
То найдется хотя бы одна такая точка, где x=c(a;b), для которой справедливо
f*(c)=f(b)-f(a)
________
b-a
ТЕОРЕМА КОШИ
Пусть функции y=f(x) и g=f(x) определены на отрезке [a;b]. Если н удовлетворяют условиям
1. непрерывна на [a;b]
2. дифференцируемы на (a;b)
3. Ɐx∈ (a;b) g*(x) ≠ 0
То найдется хотя бы 1 такая точка x=c∈ (a;b), для которой справедливо
f*(c) f(b)-f(a)
___=_____
g*(c) f(b) - g(a)
7. Следствия из теорем о среднем.
1. правило Лопиталя:
Пусть функция y=f(x) и y=g(x) определены на [a;b], если выполнены следующие условия
1. непрерывнына [a;b]
2. Дифференцируема на (a;b)
3. Ɐx∈(a;b). g*(x)≠ 0
4. f(a)=g(a)=0
Доказательсвт
функция f(x) и g(x) твечают условиям теоремы КОШИ на отрезке[a;b], ф значит и на любом меньшем отрезке [a;x]c[a;b]
8. Правило Лопиталя раскрытия неопределенностей.
Правило Лопиталя раскрывает неопределенность вида 0 делить на 0 и в случаях если
x→ a-0
x→ a
x→ - + бесконечность
Правило лопиаля остается справеливым для бесконечность делить на бескнечность
9. Условия возрастания и убывания функции. Экстремумы функции. Сформулировать необходимое и достаточное условия существования экстремума.
достаточное условия существования экстремума.
Пусть функция y=f(x) определена непрерывна и дифференцируема в некоторой окрестности точки x=c.Если выполнены следующие условия
1. f*(c) =0
2. Ɐx меньше с, f*(x) меньше 0, aⱯx Больше cf*(x) больше 0 то x=c- точка минимума; если Ɐx меньше с f*(x) больше 0, а Ɐх больше с f*(x) меньше 0 то ч=с — точка максимума
необходимое условие экстремума
Пусть функция y=f(x) определена в некоторой окрестности точки х=с. Если х=с — точка экстремума, то f* в этой точке f*(c) =0 или f*(c) – несуществует.Докв следует из теоремы ферма
10)Точки перегиба (необходимое и достаточные условия) — сформулировать.
1 достаточное
Пусть функция y=f(x) определена и непрерывна и дважды дифференцируема в окрестности точки х=с, если выполнены следующие условия
1. f **(c) = 0
2. при переходе через точку x=cf** меняет знак, то х=с — точка перегиба\
2 достаточное
Пусть функция y=f(x) определен непрервна и 2жды дифференцируема в некоторой кресстности точки х=с. ч=с является точкой максимуа если выполнены следующи условия
1. f*(c)=0
2. f**(c) меньше 0
точка х=с являтся точкой минимума если выполнено
1. f*(c) = 0
2. f**(c) больше 0
11. Выпуклость и вогнутость графика функции (определения). Условия выпуклости или вогнутости функции.
Пусть функция y=f(x) пределена, непрерывна и дифференцируема на интервале [a;b] Если точки графика функции на этом интервале расположены ниже точек любой ее касательной, то функцию называют выпухлой. Если точки графика функции расположены выше точек любой касательной а этом интервале то функция назваетсявыпухлой
производная сложной функции.пусть функция у=у(х) диффернц. на множестве х,а функция х=х(t) диффернц на множестве Т,тогда для вычисления производной сложной функции y=(y(x(t)) – y(x(t)))’=y’x*x’t
производная параметрически заданной функции.Пусть функц. задана в параллели виде у=у(t) х=х(t),где х(t) и y(t) дифференцфункц. параметра t.тогда производная y’(t) находят по формуле Y’x=y’(t):x’(t)
5)Производная показательно-степенной функции.
функция вида у=И(х)^t(x) показательно степенная.длядиффернцирования нельзя применять ни формулы для показательной функции ни формулу для степенной.
lny=lnИ(X)^t(x)
lny=t(x) * lnИ(x) невно заданная
1/у *у’=И’(x) *lnИ(x) +t(x) * 1/И(х) * И’(x)
умножим обе части на у=И(х)^t(x)
y’=(И’(x) *lnИ(x)* И(х)^t(x)+ 1/И(х) * И’(x)* И(х)^t(x)
6. Теорема Ферма. Теорема Ролля. Теорема Лагранжа. Теорема Коши (сформулировать).
ТЕОРМЕРА ФЕРМА
Пусть функция y=f(x) определена и непрерывна на отрезке [a;b]. Если в некоторой очке х=с∈ (а;b) функция достигает своего наибольшего или наименьшего значения,то если производная в этой точке существует, она равно 0⇒f*(c)=0
ТЕОРЕМА РОЛЛЯ
Пусть функция y=f(x) определена на отрезке [a;b]. если функция удовлетворяет условия
1. непрерывна на [a;b]
2. дифференцируема на (a;b)
3. f(a)=f(b)
Если выполнено условие, то найдется хотя бы 1 такая точка x=c∈ (a;b) для которой справедливо f*(c)=0
ТЕОРЕМА ЛАНГРАДЖА
Пусть функция y=f(x) определена на [a;b]. Если функция отвечает условиям:
1)непрерывна на [a;b]
2. дифференцируемана (a;b)
То найдется хотя бы одна такая точка, где x=c(a;b), для которой справедливо
f*(c)=f(b)-f(a)
________
b-a
ТЕОРЕМА КОШИ
Пусть функции y=f(x) и g=f(x) определены на отрезке [a;b]. Если н удовлетворяют условиям
1. непрерывна на [a;b]
2. дифференцируемы на (a;b)
3. Ɐx∈ (a;b) g*(x) ≠ 0
То найдется хотя бы 1 такая точка x=c∈ (a;b), для которой справедливо
f*(c) f(b)-f(a)
___=_____
g*(c) f(b) - g(a)
7. Следствия из теорем о среднем.
1. правило Лопиталя:
Пусть функция y=f(x) и y=g(x) определены на [a;b], если выполнены следующие условия
1. непрерывнына [a;b]
2. Дифференцируема на (a;b)
3. Ɐx∈(a;b). g*(x)≠ 0
4. f(a)=g(a)=0
Доказательсвт
функция f(x) и g(x) твечают условиям теоремы КОШИ на отрезке[a;b], ф значит и на любом меньшем отрезке [a;x]c[a;b]
8. Правило Лопиталя раскрытия неопределенностей.
Правило Лопиталя раскрывает неопределенность вида 0 делить на 0 и в случаях если
x→ a-0
x→ a
x→ - + бесконечность
Правило лопиаля остается справеливым для бесконечность делить на бескнечность
9. Условия возрастания и убывания функции. Экстремумы функции. Сформулировать необходимое и достаточное условия существования экстремума.
достаточное условия существования экстремума.
Пусть функция y=f(x) определена непрерывна и дифференцируема в некоторой окрестности точки x=c.Если выполнены следующие условия
1. f*(c) =0
2. Ɐx меньше с, f*(x) меньше 0, aⱯx Больше cf*(x) больше 0 то x=c- точка минимума; если Ɐx меньше с f*(x) больше 0, а Ɐх больше с f*(x) меньше 0 то ч=с — точка максимума
необходимое условие экстремума
Пусть функция y=f(x) определена в некоторой окрестности точки х=с. Если х=с — точка экстремума, то f* в этой точке f*(c) =0 или f*(c) – несуществует.Докв следует из теоремы ферма
10)Точки перегиба (необходимое и достаточные условия) — сформулировать.
1 достаточное
Пусть функция y=f(x) определена и непрерывна и дважды дифференцируема в окрестности точки х=с, если выполнены следующие условия
1. f **(c) = 0
2. при переходе через точку x=cf** меняет знак, то х=с — точка перегиба\
2 достаточное
Пусть функция y=f(x) определен непрервна и 2жды дифференцируема в некоторой кресстности точки х=с. ч=с является точкой максимуа если выполнены следующи условия
1. f*(c)=0
2. f**(c) меньше 0
точка х=с являтся точкой минимума если выполнено
1. f*(c) = 0
2. f**(c) больше 0
11. Выпуклость и вогнутость графика функции (определения). Условия выпуклости или вогнутости функции.
Пусть функция y=f(x) пределена, непрерывна и дифференцируема на интервале [a;b] Если точки графика функции на этом интервале расположены ниже точек любой ее касательной, то функцию называют выпухлой. Если точки графика функции расположены выше точек любой касательной а этом интервале то функция назваетсявыпухлой
 Вопрос 3
Основные методы интегрирования.
Непосредственное- заключается в том, чтобы использовать свойсва функции и интегралов и привести их к табличному виду
Вопрос 3
Основные методы интегрирования.
Непосредственное- заключается в том, чтобы использовать свойсва функции и интегралов и привести их к табличному виду 




 Вопрос 4
Интегрирование простейших тригонометрических функций.
Вопрос 4
Интегрирование простейших тригонометрических функций.

 Интегрирование тригонометрических функций
1°. Интегралы вида
Интегрирование тригонометрических функций
1°. Интегралы вида
 находятся с помощью тригонометрических формул
находятся с помощью тригонометрических формул
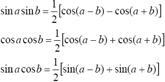 2°. Интегралы вида
2°. Интегралы вида
 где m и n - четные числа находятся с помощью формул понижения степени
где m и n - четные числа находятся с помощью формул понижения степени
 Если хотя бы одно из чисел m или n - нечетное, то полагают (пусть m = 2k + 1)
Если хотя бы одно из чисел m или n - нечетное, то полагают (пусть m = 2k + 1)
 Вопрос 5
Интегрирование иррациональных функций - Общий принцип интегрирования иррациональных выражений заключается в замене переменной, позволяющей избавиться от корней в подынтегральном выражении. Для некоторых классов функций эта цель достигается с помощью стандартных замен.
Интегралы вида
Вопрос 5
Интегрирование иррациональных функций - Общий принцип интегрирования иррациональных выражений заключается в замене переменной, позволяющей избавиться от корней в подынтегральном выражении. Для некоторых классов функций эта цель достигается с помощью стандартных замен.
Интегралы вида  , где
, где 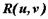 - рациональная функция своих аргументов, вычисляются заменой
- рациональная функция своих аргументов, вычисляются заменой 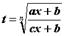 .
Интегралы вида
.
Интегралы вида  вычисляются заменой
вычисляются заменой  или
или 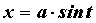 .
Интегралы вида
.
Интегралы вида  вычисляются заменой
вычисляются заменой  или
или  . Интегралы вида
. Интегралы вида  вычисляются заменой
вычисляются заменой 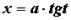 или
или  .
.


