 |
Графическое изображение вариационных рядов
|
|
|
|
Для наглядности статистические ряды представляют графиками, наиболее распространёнными являются полигон и гистограмма. Полигон применяется для изображения как дискретных, так и интервальных статистических рядов, гистограмма – для изображения только интервальных рядов. Покажем построение этих графиков на примере.
Для построения гистограммы частот на оси абсцисс откладываем частичные интервалы значений случайной величины 
, на каждом из которых строим прямоугольник, высота которого равна соответствующей частоте интервала 
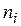. Если на гистограмме частот соединить середины верхних сторон элементарных прямоугольников, то полученная замкнутая ломаная образует полигон распределения частот (рис. 1). По гистограмме приближённо определим моду (см. подраздел 5.1).
Замечание: в теории вероятностей гистограмме и полигону относительных частот 
соответствует график функции плотности распределения. По виду полигона делают первоначальное предположение о законе распределения исследуемой случайной величины.
Рисунок 1. – Графическое изображение вариационного ряда.
4. Эмпирическая функция распределения
Пусть известен статистический ряд количественного признака X. Введем обозначения: 
– число наблюдений, при которых наблюдалось значение признака меньше 
(накопленная частота); n – объем выборки; 
– относительная частота события 
(относительная накопленная частота).
Эмпирической функцией распределения называют функцию 
, равную относительной накопленной частоте события :
.
В отличии эмпирической функции распределения выборки, интегральную функцию 
распределения генеральной совокупности называют теоретической функцией распределения. Теоретическая функция распределения определяет вероятность события : 
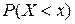, эмпирическая – относительную частоту этого события. Вследствие закона больших чисел (теорема Бернулли) относительная частота события , т.е. стремится по вероятности к вероятности этого события, т.е. к . обладает всеми свойствами , а именно:
|
|
|
1) 
;
2) – неубывающая функция;
3) =0 при 
, 
– наименьшая варианта;
4) =1 при 
, – наибольшая варианта.
Эмпирическая функция распределения выборки служит для оценки теоретической функции распределения генеральной совокупности. В столбец «Накопленная частота» таблицы 2 запишем значения, полученные по формуле: 
Таблица 2.
| Интервалы | Середина интервала
| Частота
| Накопленная частота
| Относительная накопленная частота 
|
| [6,75; 7,18) | 6,97 | 0,03 | ||
| [7,18; 7,61) | 7,40 | 0,09 | ||
| [7,61; 8,04) | 7,83 | 0,11 | ||
| [8,04; 8,47) | 8,26 | 0,25 | ||
| [8,47; 8,9) | 8,69 | 0,39 | ||
| [8,9; 9,33) | 9,12 | 0,63 | ||
| [9,33; 9,76) | 9,55 | 0,77 | ||
| [9,76; 10,19) | 9,98 | 0,89 | ||
| [10,19; 10,62) | 10,41 | 0,98 | ||
| [10,62; 11,05) | 10,84 | 1,00 |
Рисунок 2. – График эмпирической функции распределения.
Для построения графика эмпирической функции распределения (кумуляты) на оси абсцисс откладывают интервалы, на оси ординат – относительные накопленные частоты, соответствующие правым границам интервала. на левой границе первого интервала равна нулю. Кумулята представляет собой ломанную линию (рис. 2). По кумуляте приближённо определим значение медианы (см. подраздел 5.1).
Основные выборочные характеристики
К основным выборочным характеристикам относятся: средняя арифметическая, мода, медиана, дисперсия, среднее квадратическое отклонение, коэффициент вариации, коэффициент асимметрии, эксцесса. Для определения перечисленных показателей удобно составить таблицу.
Таблица 3.
| 
|
| 
| 
| 
| 
|
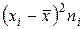
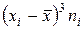
| 6,97 | 20,90 | -2,09 | 13,10 | -27,38 | 57,22 | |
| 7,40 | 44,37 | -1,66 | 16,53 | -27,44 | 45,54 | |
| 7,83 | 15,65 | -1,23 | 3,02 | -3,72 | 4,57 | |
| 8,26 | 115,57 | -0,80 | 8,96 | -7,16 | 5,73 | |
| 8,69 | 121,59 | -0,37 | 1,91 | -0,71 | 0,26 | |
| 9,12 | 218,76 | 0,06 | 0,09 | 0,01 | 0,00 | |
| 9,55 | 133,63 | 0,49 | 3,36 | 1,65 | 0,81 | |
| 9,98 | 119,70 | 0,92 | 10,16 | 9,35 | 8,60 | |
| 10,41 | 93,65 | 1,35 | 16,41 | 22,15 | 29,91 | |
| 10,84 | 21,67 | 1,78 | 6,34 | 11,28 | 20,09 | |
| 905,48 | 79,88 | -21,97 | 172,73 |
|
|
|
В зависимости от характеризуемых особенностей распределения обобщающие показатели можно разбить на три группы:
1. показатели центра распределения (центра группирования);
2. показатели степени рассеяния (вариации);
3. показатели формы распределения.
|
|
|
