Базовые данные для выполнения лабораторных работ

В.Т. Кононов, Д.С. Худяков, Г.П. Чикильдин

 

ЦИФРОВАЯ ФИЛЬТРАЦИЯ СИГНАЛОВ

 

 

Учебное пособие

для выполнения индивидуальных заданий

по дисциплине «Цифровая обработка сигналов»

для студентов АВТФ (специальность 210100)

всех форм обучения

 

Новосибирск

 

УДК 621.372.083.92 (07)

 

Рецензенты: канд. техн. наук Г.В.Сероклинов,

канд. техн. наук А.Б. Колкер

 

Данное учебное пособие составлено на базе материалов методических указаний для выполнения индивидуальных заданий по курсу «Методы цифровой фильтрации» разработанных А.С. Анисимовым и Г.П. Чикильдиным и изданных в 1995 году.

Учебное пособие содержит общие сведения о фильтрации сигналов, необходимые расчетные соотношения для проектирования различных типов нерекурсивных фильтров с линейными фазовыми частотными характеристиками на основе модифицированного гармонического ряда Фурье и рекурсивных фильтров Чебышева на базе билинейного Z-преобразованияю. Приводятся выражения для расчета частотных характеристик фильтра, соотношения для моделирования на ЦВМ нерекурсивных фильтров посредством дискретной свертки и рекурсивных фильтров по каскадной схеме, программное обеспечение проектирования и функционирования фильтров, а также примеры решения характерных модельных задач нерекурсивной и рекурсивной фильтрации

Пособие предназначено для выполнения индивидуальных заданий в рамках самостоятельной работы, практических занятий и лабораторных работ.

 

 

Новосибирский государственный технический университет, 2008 г.

ОГЛАВЛЕНИЕ

1. ОБЩИЕ СВЕДЕНИЯ О ФИЛЬТРАЦИИ…………………………………. 5

1.1. Математические модели фильтров ………………………………….. 5

1.2. Типы фильтров ……………………………………………………….. 7

1.3. Погрешности фильтрации ……………………………………………. 9

2. НЕРЕКУРСИВНЫЕ ФИЛЬТРЫ …………………………………………. 12

2.1. Проектирование фильтра …………………………………………….. 12

2.2. Характеристики фильтра …………………………………………….. 14

2.3. Функционирование фильтра …………………………………………. 14

3. РЕКУРСИВНЫЕ ФИЛЬТРЫ …………………………………………….. 16

3.1. Проектирование фильтра …………………………………………….. 16

3.2. Характеристики фильтра …………………………………………….. 22

3.3. Функционирование фильтра …………………………………………. 22

4. ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ ……………………………………….. 24

4.1. Общие положения …………………………………………………….. 24

4.2. Базовые данные для выполнения лабораторных работ …………….. 27

4.3. Лабораторная работа № 1.

Проектирование нерекурсивного фильтра ………………………….. 28

4.4. Лабораторная работа № 2.

Функционирование нерекурсивного фильтра ………………………. 31

4.5. Лабораторная работа № 3.

Проектирование рекурсивного фильтра …………………………….. 33

4.6. Лабораторная работа № 4.

Функционирование рекурсивного фильтра …………………………. 36

4.7. Расчетно-графическая работа. Расчет нерекурсивного фильтра

на базе модифицированного гармонического ряда Фурье …………. 38

5. ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ ФИЛЬТРАЦИИ …………………… 43

6. ПРИМЕРЫ ЦИФРОВОЙ ОБРАБОТКИ СИГНАЛОВ …………………... 48

6.1. Общие положения …………………………………………………….. 48

6.2. Нерекурсивный спектральный анализ ………………………………. 48

6.3. Нерекурсивное сглаживание ………………………………………… 52

6.4. Нерекурсивное дифференцирование ………………………………… 53

6.5. Рекурсивный спектральный анализ …………………………………. 55

6.6. Рекурсивное сглаживание ……………………………………………. 57

 

1. ОБЩИЕ СВЕДЕНИЯ О ФИЛЬТРАХ

1.1. Математические модели фильтров

Основными задачами фильтрации являются:

1) спектральный анализ сигнала, т.е. выделение совокупности гармонических составляющих определенного диапазона частот;

2) сглаживание сигнала, т.е. уменьшение в реализации сигнала уровня высокочастотных составляющих аддитивной помехи;

3) дифференцирование сигнала, зашумленного аддитивной помехой с высокочастотными составляющими.

Указанные и другие задачи решаются путем применения различ­ных линейных фильтров, представляющих собой линейные динамичес­кие звенья. В зависимости от характера обрабатываемого сигнала различают (см. рис.1.1) непрерывные (на входе и выходе действуют непрерывные сигналы ( и ) и дискретные (на входе и выходе действуют диск­ретные сигналы и , , - шаг дискретизации по времени) фильтры. Последние разделяются на рекурсивные и нерекур­сивные фильтры. При реализации дискретных фильтров на базе цифро­вой вычислительной техники возникает эффект конечной разрядности чисел и такие фильтры принято называть цифровыми фильтрами.

Математическими моделями фильтров служат соотношения или уравнения, устанавливающие связь между входным и выходным сигналами фильтра.

Математической моделью непрерывного фильтра является линей­ное дифференциальное уравнение n -го порядка

,

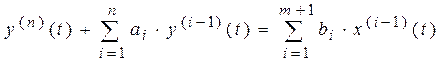или соответствующая ему дробно-рациональная передаточная функция

,

где и 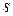- оператор и переменная преобразования Лапласа;

- импульсная характеристика фильтра,

а также интегральное уравнение свертки

.

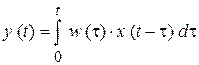Математической моделью рекурсивного фильтра является линей­ное раз­ностное уравнение -го порядка

, ,

представляющее дискретный аналог дифференциального уравнения, или соответствующая ему дробно-рациональная дискретная передаточная функция

, , ,

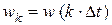где и - оператор и переменная Z-преобразования.

Математической моделью нерекурсивного фильтра является диск­ретная форма интегрального уравнения свертки –

,

причем импульсная характеристика нерекурсивного фильтра финитна, т.е. имеет конечную длительность

при , при ,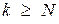

и его передаточная функция записывается в виде

. (1.1)

Амплитудная частотная характеристика (АЧХ) и фазовая частот­ная характеристика (ФЧХ) непрерывных фильтров являются непериоди­ческими функциями частоты и определяются на интервале . Частотные характеристики дискретных фильтров представляют собой периодические с периодом , , функции частоты , в ре­зультате чего они полностью определяются на интервале .

 

Типы фильтров

В зависимости от характера обработки входного сигнала фильт­ры обладают различными АЧХ. При атом могут быть выделены четыре основных типа фильтров (низкочастотный (НЧФ), полосовой (ПФ), режекторный (РФ) и высокочастотный (ВЧФ) фильтры), а также пред­ставляющий значительный практический интерес дифференцирующий фильтр (ДФ). Идеализированные АЧХ данных дискретных фильт­ров в интервале частот приведены на рис.1.2 1.6, соот­ветственно.

На каждой АЧХ выделяются следующие полосы:

1) полоса пропускания

для НЧФ и ДФ , для ПФ ,

для РФ и 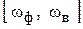, для ВЧФ ;

2) переходная полоса

для НЧФ и ДФ , для ПФ и ,

для РФ и 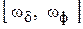, для ВЧФ ;

3) полоса задерживания

для НЧФ и ДФ , для ПФ и ,

для РФ , для ВЧФ .

Исходными данными при проектировании фильтра, полностью оп­ределяющими вид и качество его АЧХ, являются следующие параметры:

1) относительная неравномерность в полосе пропускания;

2) относительная неравномерность в полосе задерживания;

3) ширина переходных полос;

 

 

Рис. 1.2 Рис. 1.3

 

Рис. 1.4 Рис. 1.5

 

 

Рис. 1.6

 

4) верхняя граничная частота полосы пропускания;

5) нижняя граничная частота полосы пропускания;

6) коэффициент усиления в полосе пропускания;

7) шаг дискретизации по времени .

Граничные частоты и характеризуют тип фильтра и конк­ретный вид его идеальной АЧХ (при , , ).

Относительные неравномерности и характеризуют ширину , и зон допустимых изменений реальной АЧХ фильтра в полосах пропускания и задерживания, а тем самым, совместно с ши­риной переходных полос, определяют качество АЧХ фильтра. С уменьшением , и качество фильтра улучшается.

При проектировании фильтра удобно характеризовать ширину переходных полос АЧХ через относительный параметр в виде

для РФ,

для НЧФ,

для ВЧФ.

для ПФ,

(1.2)

 

1.3. Погрешности фильтрации

При функционировании фильтра всегда возникает ошибка фильтрации, обусловленная отличием реального выходного сигнала фильтра от желаемого и порожденная непременно присутствующими погрешностями фильтрации. Рассмотрим погрешности фильтрации на примере задачи сглаживания измеренной реализации сигнала , искаженной высокочастотной помехой . Сглаживание осуществляется посредством НЧФ с АЧХ , полоса пропускания которой совпадает с эффективной полосой амплитудного частотного спектра сигнала и не заходит в эффективную полосу амплитудного частотного спектра помехи (см. рис. 1.7). В этом случае выходной сигнал должен воспроизводить сигнал , а ошибка фильтрации возникает из-за следующих для определенности поименованных погрешностей.

 

Рис. 1.7

1. Переходная погрешность возникает по причине динамических свойств фильтра и может достигать на интервале длительности переходного процесса фильтра особенно больших значений. В непрерывных и рекурсивных фильтрах при эта погрешность принимает малые значения, уменьшающиеся с увеличением времени , а в нерекурсивных фильтрах из-за конечной длительности их импульсных характеристик при данная погрешность вообще отсутствует.

2. Шумовая погрешность обусловлена наличием составляющих частотного спектра помехи вне полосы пропускания АЧХ и уменьшается при уменьшении параметров и .

3. Смешанная погрешность обусловлена наличием составляющих частотного спектра сигнала вне полосы пропускания АЧХ и частотного спектра помехи в полосе пропускания АЧХ. При спектральном анализе эта погрешность отсутствует, а при сглаживании и дифференцировании ее уменьшение достигается выбором оптимального значения частоты .

4. Амплитудная погрешность возникает из-за не идеальности АЧХ в полосе пропускания и уменьшается при уменьшении параметра .

5. Фазовая погрешность обусловлена не идеальностью ФЧХ в полосе пропускания АЧХ. Если ФЧХ является строго линейной в полосе пропускания АЧХ, т.е. в этой полосе

,

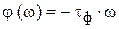то при введении в выходной сигнал фильтра запаздывания на величину фазовая погрешность полностью исключается. Отсюда возможность уменьшения уровня этой погрешности определяется степенью линейности ФЧХ, которую принято характеризовать степенью постоянства групповой или фазовой задержек фильтра в полосе пропускания АЧХ.

6. Дискретная погрешность может возникать из-за дискретизации по времени обрабатываемой реализации, что порождает эффекты отражения и наложения периодических частотных спектров и требует выбора достаточно малого шага дискретизации по времени .

7. Цифровая погрешность обусловлена конечной разрядностью представления чисел при цифровой реализации фильтра.

Уменьшение цифровой погрешности прямо связано с возможностями используемой вычислительной техники. Обеспечение требуемого уровня шумовой, смешанной, амплитудной и дискретной погрешностей достигается соответствующим выбором априори задаваемых параметров , , , и . При этом с уменьшением параметров , , и возрастает необходимый объем оперативной памяти и количество вычислений, а тем самым возможности уменьшения шумовой, амплитудной и дискретной погрешности также ограничены возможностями используемой вычислительной техники.

 

2. НЕРЕКУРСИВНЫЕ ФИЛЬТЫ

2.1. Проектирование фильтра

Проектирование нерекурсивного фильтра сводится к синтезу его передаточной функции при которой АЧХ фильтра удовлетворяет поставленным в исходных данных требованиям. Согласно выражению (1.1) передаточная функция нерекурсивного фильтра полностью определяется 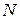отсчетами , , его импульсной характеристики. Если импульсная характеристика фильтра является симметричной или антисимметричной относительно некоторой оси симметрии, то такой фильтр обладает линейной ФЧХ. На основе аппроксимации идеальной АЧХ фильтра модифицированным гармоническим рядом Фурье могут быть синтезированы фильтры только вида 1 или вида 2, характеризующиеся нечетным значением величины

, ,

и необходимостью выполнения дополнительного условия

.

Фильтры вида 1 реализуют НЧФ, ПФ, РФ, и ВЧФ и описываются передаточной функцией

, (2.1)

а фильтры вида 2 реализуют только ДФ и описываются функцией

. (2.2)

Синтез передаточной функции или, что то же самое, импульсной характеристики 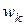, , при использовании сглаживающих множителей Кайзера производится в следующем порядке.

1. Определяется согласно выражениям (1.2) ширина переходных
полос АЧХ фильтра.

2. Вычисляется параметр 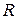множителей Кайзера

,

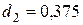где , при ,

, при .

3. Определяется число членов аппроксимирующего ряда Фурье

,

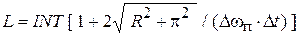где - оператор выделения целой части числа.

4. Находится совокупность сглаживающих множителей Кайзера

, ,

причем значения модифицированной функции Бесселя первого рода нулевого порядка определяются в виде конечной суммы ряда

.

5. Вычисляются с учетом вводимых обозначений

, , ,

, , ,

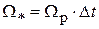искомые отсчеты 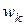, , 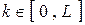импульсной характеристики:

1) для НЧФ ,

, ;

2) для ПФ ,

, ;

3) для РФ ,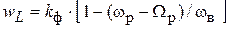

, ;

4) для ВЧФ ,

, ;

5) для ДФ

, .

 

2.2. Характеристики фильтра

Осуществляя в передаточной функции замену

,

получаем согласно выражениям (2.1) и (2.2) следующие расчетные соотношения для АЧХ и ФЧХ фильтра в диапазоне частот :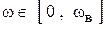

1) в случае НЧФ, ПФ, РФ, и ВЧФ

,

;

2) в случае ДФ

,

.

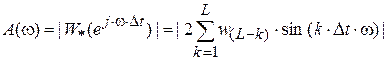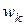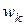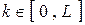Свойства фильтра во временной области непосредственно описываются импульсной характеристикой , , причем отсчеты , , определяются при проектировании фильтра, а отсчеты 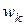, , находятся согласно свойств симметрии:

1) в случае НЧФ, ПФ, РФ, ВЧФ

, ;

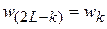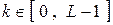2) в случае ДФ

, .

 

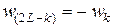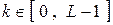2.3. Функционирование фильтра

Вычисление дискретного значения выходного сигнала фильтра в -й момент времени по дискретным значениям входного сигнала и импульсной характеристики 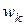производится в соответствии со следующими расчетными соотношениями:

1) в случае НЧФ, ПФ, РФ и ВЧФ согласно выражению (2.1)

;

2) в случае ДФ согласно выражению (2.2)

,

причем в процессе вычислений необходимо полагать

при .

 

3. РЕКУРСИВНЫЕ ФИЛЬТРЫ

 

3.1. Проектирование фильтра

Проектирование рекурсивного фильтра сводится к синтезу его передаточной функции , при которой АЧХ фильтра удовлетворяет предъявляемым требованиям в исходных данных. При использовании билинейного Z -преобразования принимается

(3.1)

и проектирование фильтра, реализуемого по каскадной схеме, предлагает последовательный синтез трех передаточных функций:

1) функции 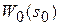низкочастотного фильтра прототипа;

2) функции 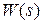требуемого непрерывного фильтра;

3) функции требуемого рекурсивного фильтра.

Передаточная функция низкочастотного фильтра-прототипа Чебышева характеризуется порядком и представляется в форме

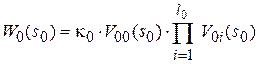(3.2)

где

при ,

при ,

.

Синтез функции 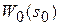осуществляется на основании:

- неравномерности АЧХ в полосе пропускания;

- неравномерности АЧХ в полосе задержания;

- параметра , определяющего ширину переходных полос АЧХ, и предусматривает последовательное определение:

1) вспомогательных параметров

, ;

2) порядка передаточной функции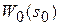

;

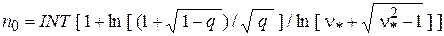3) количества

пар комплексно-сопряженных полюсов

, , ,

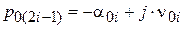передаточной функции ;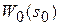

4) вспомогательного параметра

;

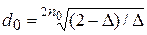5) вещественных и мнимых частей комплексных полюсов

,

, ;

6) дополнительного при вещественного полюса

, ;

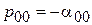7) других параметров передаточной функции

, ,

при

при ,

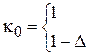
Передаточная функция требуемого непрерывного фильтра представляется в форме

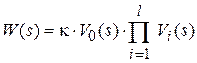, (3.3)

где

,

при ,

при для ПФ и РФ.

при для НЧФ и ВЧФ,

Синтез функции 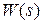осуществляется на основании:

- верхней граничной частоты полосы пропускания АЧХ;

- верхней граничной частоты полосы пропускания АЧХ;

- коэффициента усиления в полосе пропускания АЧХ;

- шага дискретизации по времени

посредством предварительного определния:

1) параметра

;

2) количества

для ПФ и РФ,

для НЧФ и ВЧФ,

пар комплексно-сопряжных полюсов

, , ,

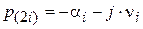передаточной функции ;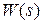

3) расчетных верхней и нижней граничных частот скорректированной полосы пропускания АЧХ

, ,

и последующей, соответствующей для каждого типа фильтра, замены аргумента в передаточной функции вида (3.2).

В случае НЧФ с учетом замены

находим

, ,

, , , .

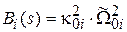В случае ПФ с учетом замены

, , ,

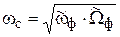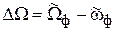находим

, , ,

, ,

, ,

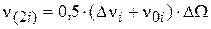где

, ,

, , ,

, .

В случае РФ с учетом замены

, , ,

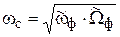и обозначений

,

находим

, , ,

, ,

, ,

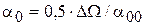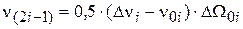где

, ,

, , ,

, .

В случае ВЧФ с учетом замены

находим

, ,

, , , .

Передаточная функция требуемого рекурсивного фильтра представляется в форме

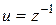, (3.4)

где

,

при для НЧФ и ВЧФ,

при ,

при для ПФ и РФ,

Синтез функции осуществляется путем непосредственной замены аргумента 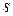в функции 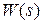вида (3.3) согласно выражению

,

получаемого непосредственно из билинейного Z-преобразования (3.1).

Такая замена с учетом обозначений

, ,

приводит к последующим расчетным соотношениям:

,

,

а также при ;

1) в случае НЧФ и ВЧФ

,

2) в случае ПФ и РФ

,

и дополнительно:

1) в случае НЧФ

, , , ,

, ;

2) в случае ПФ

,

, ,

, , , , ;

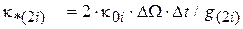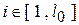3) в случае РФ
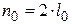