 |
Расчет нерекурсивного фильтра на основе модифицированного гармонического ряда Фурье
|
|
|
|
Цель работы.
Приобретение навыков проектирования и расчета нерекурсивных фильтров.
Постановка задачи.
В соответствии с исходными данными (табл. 4.3) определить параметры цифрового нерекурсивного фильтра (количество L отсчетов ИХ, параметры и значения сглаживающих множителей, значения отсчетов ИХ, АЧХ и ФЧХ) и по полученным данным построить графики сглаживающих множителей, ИХ, АЧХ и ФЧХ. Типы сглаживающих множителей  и их аналитические выражения приведены в табл. 4.4.
и их аналитические выражения приведены в табл. 4.4.
Дополнительное задание.
Осуществить спектральный анализ либо дифференцирование сигнала (в зависимости от типа спроектированного фильтра).
В спектральном анализе входной сигнал формируется из синусоидальных гармоник, числом равным числу участков полос пропускания и задерживания (т.е. 2 либо 3 гармоники в зависимости от типа спроектированного фильтра). Гармоники должны попадать в каждую из полос.
При дифференцировании входной сигнал следует формировать в виде суммы двух синусоидальных гармоник, одна из которых попадает в полосу пропускания фильтра, а вторая лежит за ее пределами.
После соответствующей обработки (спектральный анализ или дифференцирование) осуществить коррекцию выходного сигнала с целью получения минимального значения погрешностей за счет удаления переходной и фазовой составляющих ошибки фильтрации.
Таблица 4.3
| № | Тип |  р/с р/с
|  р/с р/с
|  р/с р/с
| 

| 
| 
| Тип сглаживающих множителей 
| ФИО |
| НЧФ ПФ РФ ВЧФ ДФ НЧФ ПФ РФ ВЧФ ДФ НЧФ ПФ РФ ВЧФ ДФ НЧФ ПФ РФ ВЧФ ДФ НЧФ ПФ РФ ВЧФ ДФ НЧФ ПФ РФ ВЧФ ДФ НЧФ ПФ РФ ВЧФ ДФ НЧФ ПФ РФ ВЧФ ДФ | - 1.0 5.0 1.0 - - 3.0 6.0 3.0 - - 2.0 5.0 5.0 - - 7.0 10.0 7.0 - - 9.0 12.0 9.0 - - 12.0 15.0 12.0 - - 15.0 18.0 15.0 - - 18.0 21.0 18.0 - | 1.0 5.0 1.0 - 1.0 3.0 6.0 3.0 - 3.0 5.0 5.0 2.0 - 5.0 7.0 10.0 7.0 - 7.0 9.0 12.0 9.0 - 9.0 12.0 15.0 12.0 - 12.0 15.0 18.0 15.0 - 15.0 18.0 21.0 18.0 - 18.0 | 0.5 1.0 1.5 0.5 1.0 1.5 0.5 1.0 1.5 0.5 1.0 1.5 0.5 1.0 1.5 0.5 1.0 1.5 0.5 1.0 1.5 0.5 1.0 1.5 0.5 1.0 1.5 0.5 1.0 1.5 0.5 1.0 1.5 0.5 1.0 1.5 0.5 1.0 1.5 0.5 | 0.2 0.1 0.01 0.02 0.2 | 0.5 1.0 1.5 0.5 1.0 1.5 0.5 1.0 1.5 0.5 1.0 1.5 0.5 1.0 1.5 0.5 1.0 1.5 0.5 1.0 1.5 0.5 1.0 1.5 0.5 1.0 1.5 0.5 1.0 1.5 0.5 1.0 1.5 0.5 1.0 1.5 0.5 1.0 1.5 0.5 | 0.2 0.1 0.1 0.2 0.1 0.1 0.2 0.1 0.1 0.2 0.1 0.1 0.2 0.1 0.1 0.2 0.1 0.1 0.2 0.1 0.1 0.2 0.1 0.1 0.2 0.1 0.1 0.2 0.1 0.1 0.2 0.1 0.1 0.2 0.1 0.1 0.2 0.1 0.1 0.2 | Кайзера единичные Бартлетта Парзена Ланцоша Хэмминга Хэннинга Блэкмана Кайзера единичные Бартлетта Парзена Ланцоша Хэмминга Хэннинга Блэкмана Кайзера единичные Бартлетта Парзена Ланцоша Хэмминга Хэннинга Блэкмана Кайзера единичные Бартлетта Парзена Ланцоша Хэмминга Хэннинга Блэкмана Кайзера единичные Бартлетта Парзена Ланцоша Хэмминга Хэннинга Блэкмана | Афанасьев Зворыгина Шигорова Кондратьев Котович Кокошкина Евдокимова Маевский И. Маевский А. Стекленев Новиков |
Продолжение Таблицы 4.3
|
|
|
| НЧФ ПФ РФ ВЧФ ДФ РФ ПФ ВЧФ НЧФ ДФ РФ ПФ | - 21.0 24.0 21.0 - 10.0 14.0 24.0 - - 19.0 13.5 | 21.0 24.0 21.0 - 21.0 6.5 19.0 - 23.0 22.0 13.0 17.5 | 1.0 1.5 0.5 1.0 1.5 1.0 1.0 1.5 1.0 1.5 1.5 1.0 | 0.05 0.03 | 1.0 1.5 0.5 1.0 1.5 1.5 1.0 1.5 0.5 1.0 1.5 1.0 | 0.1 0.1 0.2 0.1 0.1 0.1 0.2 0.1 0.2 0.2 0.1 0.1 | Кайзера единичные Бартлетта Парзена Ланцоша Хэмминга Хэннинга Блэкмана Кайзера единичные Бартлетта Парзена |
 в вариантах с множителями Кайзера задан параметр
в вариантах с множителями Кайзера задан параметр  , в остальных – L.
, в остальных – L.
Таблица 4.4
| Тип множителя | Аналитическое выражение 
|
| Бартлетта | 
|
| Ланцоша |  , , 
|
| Хэмминга, Хэннинга |  , ,
 - множители Хэмминга, - множители Хэмминга,
 - множители Хэннинга (Ханна) - множители Хэннинга (Ханна)
|
| Блэкмана | 
|
| Кайзера |  , , 
 - модифицированная функция Бесселя
первого рода нулевого порядка. - модифицированная функция Бесселя
первого рода нулевого порядка.
|
| Парзена | 

|
|
|
|
Содержание пояснительной записки.
В пояснительной записке обязательно должны быть приведены:
1) исходные данные в соответствии с вариантом (все используемые в расчетах);
2) формульные выражения для расчетов и значения
· числа членов аппроксимирующего ряда Фурье,
· параметров сглаживающих множителей и совокупность их значений в виде таблицы,
· ИХ, АЧХ и ФЧХ в виде таблиц,
· выходного сигнала (таблица), полученного при решении задачи спектрального анализа или дифференцирования (только при выполнении дополнительного задания);
3) рассчитанное значение фазовой задержки;
4) графики ИХ, АЧХ и ФЧХ спроектированного фильтра, а также (только для дополнительного задания)графики входного, выходного идеального, не скорректированного и скорректированнного сигналов;
5) выводы о соответствии полученных параметров характеристик фильтра требуемым данным согласно задания, а также (только для дополнительного задания) о соответствии выходного сигнала идеальному;
6) листинг программы.
Таким образом, в пояснительной записке должны содержаться 3 таблицы и 3 графика по основному заданию и 4 графика на одном рисунке по дополнительному заданию.
Примечания.
1. Расчетно-графическая работа выполняется посредством составления программы на одном из широко используемых языков программирования, подходящих для решения вычислительных задач (FORTRAN, C, C++, VBA) и выполнением ее на компьютере. Допускается отсутствие в программе операторов ввода и жесткая в соответствии с вариантом структура. В тексте программы должны присутствовать поясняющие комментарии;
2. Пояснительная записка должна быть оформлена в соответствии с существующими требованиями к оформлению отчетов по лабораторным работам. Размер графиков – половина страницы, аргументом должны являться физические величины, а не номера отсчетов;
3. При выполнении расчетов следует использовать только данное учебное пособие и никакое другое во избежание ошибок, поскольку в другом пособии формульные выражения могут несколько отличаться из-за применения другой методики расчетов;
|
|
|
4. Если в формулах, прямой расчет принципиально невозможен (например, бесконечные ряды), следует отразить в отчете предложенный способ выхода из такой ситуации и обосновать его. В случае необходимости использования каких-либо дополнительных параметров следует указать, как и откуда они берутся, и привести соответствующие расчеты;
5. С целью более глубокого усвоения материала курса некоторые варианты заданий содержат данные, делающие процедуру проектирования фильтра с заданными требованиями невыполнимой. В этом случае рекомендуется убедиться в правильности работы составленной программы, а затем обнаружить и изменить некорректно заданные параметры так, чтобы вычисления стали возможными. Не следует изменять корректируемый параметр больше, чем этого требуется для осуществления расчетов. Максимальное изменение – не более чем в два раза. Отразить эти обстоятельства в отчете. В случае получения фильтра с характеристиками, не соответствующими заданным, следует поступать аналогичным образом, однако в отчете наряду со скорректированными характеристиками необходимо привести также и графики ИХ, АЧХ и ФЧХ для изначально спроектированного по исходным данным фильтра;
6. Графики сигналов строить по окончании переходного процесса фильтра. Интервал определения выходного сигнала должен соответствовать периоду самой низкочастотной гармоники входного сигнала;
5. ПРОГРАМНОЕ ОБЕСПЕЧЕНИЕ ФИЛЬТРАЦИИ
Программное обеспечение фильтрации выполнено в виде пакета FILTR, работающего в режимах проектирования и функционирования фильтра.
В режиме проектирования фильтра производится:
1) синтез ИХ  ,
,  , требуемого нерекурсивного фильтра или передаточной функции
, требуемого нерекурсивного фильтра или передаточной функции 
 требуемого рекурсивного фильтра по задаваемым исходным данным
требуемого рекурсивного фильтра по задаваемым исходным данным  ,
,  ,
,  ,
,  ,
,  ,
,  и
и  ;
;
2) вычисление массива отсчетов АЧХ 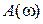 и ФЧХ
и ФЧХ  фильтра в задаваемом диапазоне частот
фильтра в задаваемом диапазоне частот  с выбранным шагом дискретизации по частоте
с выбранным шагом дискретизации по частоте  ;
;
3) линейную аппроксимацию ФЧХ  в полосе пропускания АЧХ
в полосе пропускания АЧХ  и определение приближенного значения фазовой задержки
и определение приближенного значения фазовой задержки  при рекурсивной фильтрации;
при рекурсивной фильтрации;
|
|
|
4) вычисление массива отсчетов временной характеристики  в задаваемом диапазоне времени
в задаваемом диапазоне времени  с выбранным шагом дискретизации по времени
с выбранным шагом дискретизации по времени  и определение по задаваемому уровню
и определение по задаваемому уровню  эффективной длительности
эффективной длительности  переходного процесса рекурсивного фильтра.
переходного процесса рекурсивного фильтра.
В режиме функционирования производится:
1) формирование массива отсчетов входного сигнала  и эталонного выходного сигнала
и эталонного выходного сигнала  в задаваемом диапазоне времени
в задаваемом диапазоне времени 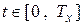 с задаваемым шагом дискретизации по времени
с задаваемым шагом дискретизации по времени  ;
;
2) синтез ИХ  ,
,  , требуемого нерекурсивного фильтра или передаточной функции
, требуемого нерекурсивного фильтра или передаточной функции  требуемого рекурсивного фильтра по задаваемым исходным данным
требуемого рекурсивного фильтра по задаваемым исходным данным  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ;
;
3) вычисление массива отсчетов выходного сигнала  в диапазоне времени
в диапазоне времени  с шагом дискретизации
с шагом дискретизации  ;
;
4) вычисление относительных среднеквадратических ошибок фильтрации 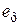 и
и  .
.
Программа FILTR работает в оконном режиме. В программе задаются следующие параметры:
режим работы, а именно:
· проектирование фильтра,
· функционирование фильтра;
вид фильтра, а именно:
· нерекурсивный фильтр,
· рекурсивный фильтр;
тип фильтра, а именно:
· низкочастотный фильтр (НЧФ),
· полосовой фильтр (ПФ),
· режекторный фильтр (РФ),
· высокочастотный фильтр (ВЧФ),
· дифференцирующий фильтр (ДФ);
шаг дискретизации по времени 
 ;
;
в зависимости от режима работы:
1) в режиме проектирования фильтра:
· шаг дискретизации по частоте 
 ;
;
· нижняя частота 
 диапазона определения АЧХ и ФЧХ;
диапазона определения АЧХ и ФЧХ;
· верхняя частота 
 диапазона определения АЧХ и ФЧХ;
диапазона определения АЧХ и ФЧХ;
и дополнительно при рекурсивной фильтрации:
· уровень  , определяющий эффективную длительность временной характеристики
, определяющий эффективную длительность временной характеристики  ;
;
· длительность  определения временной характеристики
определения временной характеристики  ;
;
2) в режиме функционирования фильтра:
тип модельной задачи, а именно:
· спектральный анализ сигнала;
· сглаживание сигнала;
· дифференцирование сигнала;
основная длительность 
 интервала фильтрации;
интервала фильтрации;
в зависимости от вида фильтрации:
1) при нерекурсивной фильтрации:
· параметр L длительности ИХ;
2) при рекурсивной фильтрации:
· эффективная длительность 
 переходного процесса фильтра;
переходного процесса фильтра;
· фазовая задержка фильтра 
 ;
;
в зависимости от типа модельной задачи:
1) при спектральном анализе сигнала:
индекс, определяющий эталонный выходной сигнал, а именно:
· 1 – при  ,
,
· 2 – при  ,
,
· 3 – при  ,
,
· 4 – при  ,
,
· 5 – при  ,
,
· 6 – при  ;
;
2) при сглаживании и дифференцировании сигнала:
· уровень  помехи
помехи  ;
;
· нижняя частота 
 эффективной полосы частотного спектра помехи
эффективной полосы частотного спектра помехи  ;
;
· верхняя частота 
 эффективной полосы частотного спектра помехи
эффективной полосы частотного спектра помехи  ;
;
· ширина 
 переходных полос АЧХ фильтра, формирующего помеху
переходных полос АЧХ фильтра, формирующего помеху  ,
,
а также при любом режиме работы:
|
|
|
· неравномерность  АЧХ фильтра в полосе пропускания;
АЧХ фильтра в полосе пропускания;
· неравномерность  АЧХ фильтра в полосе задерживания;
АЧХ фильтра в полосе задерживания;
· параметр  , определяющий ширину переходных полос АЧХ;
, определяющий ширину переходных полос АЧХ;
· верхняя граничная частота 
 полосы пропускания АЧХ фильтра в случае НЧФ, ПФ, РФ и ДФ;
полосы пропускания АЧХ фильтра в случае НЧФ, ПФ, РФ и ДФ;
· нижняя граничная частота 
 полосы пропускания АЧХ фильтра в случае ПФ, РФ и ВЧФ;
полосы пропускания АЧХ фильтра в случае ПФ, РФ и ВЧФ;
· коэффицент усиления  в полосе пропускания АЧХ фильтра.
в полосе пропускания АЧХ фильтра.
Выходными параметрами программы являются следующие:
1) в режиме проектирования фильтра
при нерекурсивной фильтрации:
- L – параметр L длительности ИХ;
- W (K) – массив отсчетов ИХ  ,
,  ;
;
при рекурсивной фильтрации:
- Y (K) – массив отсчетов переходной (временной) характеристики фильтра  ,
,  ,
,  , где
, где  – количество отсчетов эффективной длительности временной характеристики, фазовой задержки и интервала наблюдения выходного сигнала фильтра соответственно;
– количество отсчетов эффективной длительности временной характеристики, фазовой задержки и интервала наблюдения выходного сигнала фильтра соответственно;
и при любом виде фильтрации:
- A (K) – массив отсчетов АЧХ фильтра  ,
,  ;
;
- F (K) – массив отсчетов ФЧХ фильтра  ,
,  ;
;
2) в режиме функционирования фильтра
- X (K) – массив отсчетов входного сигнала фильтра  ,
,  ;
;
- Y (K) – массив отсчетов выходного сигнала фильтра  ,
,  ;
;
- Z (K) – массив отсчетов скорректированного выходного сигнала фильтра  ,
,  ;
;
- V (K) – массив отсчетов эталонного выходного сигнала фильтра  ,
,  ;
;
- EY – ошибка фильтрации 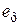 ;
;
- EZ – скорректированная ошибка фильтрации  .
.
Выходные параметры программы FILTR записываются в файлы данных. Структура файлов такова, что помимо комментариев каждый файл содержит соответствующее количество колонок. Первая колонка представляет собой порядковый номер элементов массива данных. Во второй колонке расположены значения аргумента (время в  для временных характеристик фильтра и сигналов или частота в
для временных характеристик фильтра и сигналов или частота в  для частотных характеристик), а далее следуют колонки, содержащие значения соответствующих функций.
для частотных характеристик), а далее следуют колонки, содержащие значения соответствующих функций.
В файл impuls.txt записывается массив ИХ нерекурсивного фильтра – F (K),  .
.
В файл perehod.txt записывается массив переходной характеристики рекурсивного фильтра – Y (K),  .
.
В файл characts.txt записываются массивы частотных характеристик фильтра: AЧХ и ФЧХ,  .
.
В файл signals.txt записываются массивы сигналов X (K), Y (K), Z (K), V (K),  .
.
В программе FILTR предусмотрена возможность графического изображения данных на экране монитора с последующим сохранением графиков в файл или буфер обмена.
6. ПРИМЕРЫ ФИЛЬТРАЦИИ
6.1. Общие положения
Ниже приведены примеры нерекурсивной и рекурсивной фильтрации сигнала  при фиксированных значениях ряда параметров
при фиксированных значениях ряда параметров  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  .
.
На рис. 6.1 показан отрезок входного сигнала  вида (4.2), используемого при решении задач спектрального анализа, а на рис. 6.2 и рис. 6.3
вида (4.2), используемого при решении задач спектрального анализа, а на рис. 6.2 и рис. 6.3
 |
Рис. 6.1
представлены отрезки входного сигнала  вида (4.1), содержащего случайную помеху
вида (4.1), содержащего случайную помеху  вида (4.3) и эталонного выходного сигнала
вида (4.3) и эталонного выходного сигнала  вида (4.4), используемых при решении задач сглаживания (рис. 6.2) и дифференцирования (рис. 6.3).
вида (4.4), используемых при решении задач сглаживания (рис. 6.2) и дифференцирования (рис. 6.3).
6.2. Нерекурсивный спектральный анализ
Рассмотрим задачу выделения из сигнала  вида (4.2), слагаемой
вида (4.2), слагаемой  .
.
Поставленная задача спектрального анализа сигнала  может быть
может быть
решена посредством использования, например, ВЧФ, проектируемого по следующим исходным данным:
 ,
,  ,
,  .
.
При проектировании фильтра получаем  .
.

Рис. 6.2

Рис. 6.3
Графики ИХ, АЧХ и ФЧХ фильтра приведены на рис. 6.4 – рис. 6.6.
На рис. 6.7 показаны отрезки сигналов  ,
,  и
и  , причем ошибки фильтрации составляют
, причем ошибки фильтрации составляют
 ,
,  .
.
Ошибки фильтрации порождаются следующими факторами:
1) не идеальностью АЧХ фильтра  , обусловленной ненулевыми неравномерностями
, обусловленной ненулевыми неравномерностями  и
и  в полосах пропускания и задерживания и ненулевой шириной
в полосах пропускания и задерживания и ненулевой шириной  переходной полосы АЧХ фильтра;
переходной полосы АЧХ фильтра;
2) не идеальностью ФЧХ фильтра  (ошибка
(ошибка 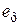 );
);
3) ненулевыми значениями амплитудного спектра  полезной составляющей
полезной составляющей  вне полосы пропускания АЧХ фильтра;
вне полосы пропускания АЧХ фильтра;
4) ненулевыми значениями амплитудного спектра  помехи
помехи  вне полосы задерживания АЧХ фильтра;
вне полосы задерживания АЧХ фильтра;
5) конечной разрядностью чисел в используемой ЦВМ.
 |
Рис. 6.4

|
|
|
|
Рис. 6.5 Рис. 6.6

Рис. 6.7
6.3. Нерекурсивное сглаживание
Рассмотрим задачу сглаживания сигнала  вида (4.1), содержащего случайную помеху
вида (4.1), содержащего случайную помеху  вида (4.3).
вида (4.3).
Поставленная задача сглаживания сигнала  решается посредством использования НЧФ, проектируемого, например, по следующим данным:
решается посредством использования НЧФ, проектируемого, например, по следующим данным:
 ,
,  ,
,  .
.
При проектировании фильтра получаем  .
.
Графики ИХ, АЧХ и ФЧХ фильтра приведены на рис. 6.8 – рис. 6.10.
 |
Рис. 6.8

Рис. 6.9 Рис. 6.10
На рис. 6.11 показаны отрезки сигналов  ,
,  и
и  , причем ошибки фильтрации составляют
, причем ошибки фильтрации составляют
 ,
, 
и порождаются теми же факторами, что и при спектральном анализе сигнала.
 |
Рис. 6.11
6.4. Нерекурсивное дифференцирование
Рассмотрим задачу дифференцирования сигнала  вида (4.1), содержащего случайную помеху
вида (4.1), содержащего случайную помеху  вида (4.3).
вида (4.3).
Задача дифференцирования сигнала  решается посредством использования ДФ, проектируемого, например, по следующим данным:
решается посредством использования ДФ, проектируемого, например, по следующим данным:
 ,
,  ,
,  .
.
При проектировании фильтра получаем  .
.
Графики ИХ, АЧХ и ФЧХ фильтра приведены на рис. 6.12 – рис. 6.14.
На рис. 6.15 показаны отрезки сигналов  ,
,  и
и  , причем ошибки фильтрации составляют
, причем ошибки фильтрации составляют
 ,
, 
и порождаются теми же факторами, что и при спектральном анализе сигнала.
 |
Рис. 6.12
 |
Рис. 6.13 Рис. 6.14
 |
Рис. 6.15
6.5. Рекурсивный спектральный анализ
Рассмотрим задачу выделения из сигнала  вида (4.2), слагаемой
вида (4.2), слагаемой  .
.
Поставленная задача решается посредством использования РФ, проектируемого, например, по следующим исходным данным:
 ,
,  ,
,  ,
,  ,
, 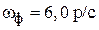 ,
,  .
.
В результате проектирования передаточная функция 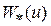 требуемого рекурсивного фильтра определяется выражением
требуемого рекурсивного фильтра определяется выражением
 ,
,  .
.
График переходной характеристики фильтра приведен на рис. 6.16, причем  .
.
Графики АЧХ и ФЧХ фильтра показаны на рис. 6.17 и рис. 6.18, причем линейная аппроксимация ФЧХ дает  .
.
На рис. 6.19 представлены отрезки сигналов  ,
,  и
и  , причем ошибки фильтрации составляют
, причем ошибки фильтрации составляют
 ,
,  .
.
 |
Рис. 6.16
 |
Рис. 6.17 Рис. 6.18

Рис. 6.19
Ошибки фильтрации порождаются вышеотмеченными в п. 4.2 пятью факторами, а также двумя дополнительными факторами:
6) бесконечной длительностью ИХ;
7) нелинейным характером ФЧХ в полосе пропускания АЧХ.
6.6. Рекурсивное сглаживание
Рассмотрим задачу сглаживания сигнала  вида (4.1), содержащего случайную помеху
вида (4.1), содержащего случайную помеху  вида (4.3).
вида (4.3).
Поставленная задача решается посредством использования НЧФ, проектируемого, например, по следующим исходным данным:
 ,
,  ,
,  ,
,  ,
,  .
.
В результате проектирования передаточная функция 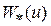 требуемого рекурсивного фильтра определяется выражением
требуемого рекурсивного фильтра определяется выражением
 ,
,  .
.
График переходной характеристики фильтра приведен на рис. 6.20, причем  .
.
Графики АЧХ и ФЧХ фильтра показаны на рис. 6.21 и рис. 6.22, причем линейная аппроксимация ФЧХ дает  .
.
На рис. 6.23 представлены отрезки сигналов  ,
,  и
и  , причем ошибки фильтрации составляют
, причем ошибки фильтрации составляют
 |
Рис. 6.20
 |
Рис. 6.21 Рис. 6.22

Рис. 6.23
 ,
,  .
.
и порождаются теми же факторами, что и при рекурсивном спектральном анализе сигнала.
|
|
|





