 |
Постановка задач линейного программирования и
|
|
|
|
Исследование их структуры
Большинство задач оптимизации, может быть сформулировано так:
максимизировать F (x1,x2,…xn)
при m ограничениях: g1 (x1,…xn)≤ b1;
g2 (x1,…xn)≤ b2;
……………….
gm (x1,…xn)≤ bm,
где F (x1,x2,…xn) – целевая функция, или критерий эффективности (например, прибыль от производства каких-либо видов продукции, стоимость перевозок и т.п); X = { x1,…xn } – варьируемые параметры; g1 (X),…, gm(X) – функции, которые задают ограничения на имеющиеся ресурсы.
Несмотря на требование линейности функций критериев и ограничений, в рамки линейного программирования попадают многочисленные задачи распределения ресурсов, управления запасами, сетевого и календарного планирования, транспортные задачи и прочие.
Рассмотрим некоторые из них.
Определение оптимального ассортимента.
Имеются m видов ресурсов в количествах b1,b2,…,bi,…, bm и n видов изделий. Задана матрица A = || aij ||, i = 1,…, n, где aij характеризует нормы расхода i -го ресурса на единицу j -го вида изделий. Эффективность производства j -го вида изделий характеризуется Cj, удовлетворяющим условию линейности. Нужно определить такой план выпуска изделий (оптимальный ассортимент), при котором суммарный показатель эффективности будет наибольший.
Обозначим количество единиц k -го вида изделий, выпускаемых предприятием, через xk, k = 1, K. Тогда математическая модель этой задачи будет иметь такой вид:
 максимизировать
максимизировать 
при ограничения 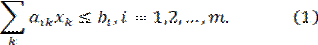
Кроме ограничений на ресурсы (1), в эту модель можно ввести дополнительные ограничения на планируемый уровень выпуска продукции x j ≥ x j0, xi: xj: xk = bi: bj: bk для всех i, j, k и т.д.
Оптимальное распределение взаимозаменяемых ресурсов.
Имеются m видов взаимозаменяемых ресурсов a1,a2,…am, используемых при выполнении n различных работ (задач). Объемы работ, которые должны быть выполнены, составляют b1,b2,…,bi,…, bn единиц. Заданы числа λ ij, указывающие, сколько единиц j- й работы можно получить из единицы i -го ресурса, а также Cij – затраты на производство j -й работы из единицы i -го ресурса. Требуется распределить ресурсы по работам таким образом, чтобы суммарная эффективность выполненных работ была максимальной (или суммарные затраты – минимальными).
|
|
|
Данная задача называется общей распределительной задачей. Количество единиц i -го ресурса, которое выделено на выполнение работ j- го вида, обозначим xij.
Математическая модель рассматриваемой задачи такова:
минимизировать

при ограничениях
 (2)
(2)
 (3)
(3)
Ограничение (2) означает, что план всех работ должен быть выполнен полностью, а (3) – что ресурсы должны быть израсходованы целиком.
Примером этой задачи может быть задача о распределении самолетов по авиалиниям.
Задача о раскрое материалов.
Пусть поступает в раскрой m различных материалов. Требуется изготовить из них k разных комплектующих изделий (комплектов) в количествах, пропорциональных величинам b1, b2,…,bk (условия комплектности). Пусть каждую единицу j -го материала j = 1,…, m можно раскроить n различными способами, так что при использовании i -го способа раскроя, i = 1,…, n получим aij единиц k -го изделия. Нужно определить план раскроя материалов, обеспечивающий максимальное количество комплектов, если имеющийся запас j -го материала составляет aj единиц.
Обозначим через xij количество единиц j -го материала, раскраиваемых i –м способом, а через x – общее количество изготавливаемых комплектов.
Математическая модель этой задачи имеет такой вид:
 (5)
(5)
 . (6)
. (6)
Условие (5) означает ограничение на запас j -го материала, а (6) – условие комплектности.
|
|
|


