Решение задачи о кратчайшем пути

Цель работы

Изучение методики выбора оптимального маршрута доставки в задачах, условия которых формализованы в виде ориентированного графа.

Краткие теоретические сведения

В повседневной практике часто возникают задачи, связанные с перемещением материальных объектов из одного пункта в другой, причем для этого существует множество возможных маршрутов, состоящих из последовательности пунктов. Задача заключается в нахождении оптимального маршрута, перемещение по которому потребует наименьших затрат.

Условия задачи можно формализовать в виде взвешенного ориентированного графа (орграфа). Например, для выбора оптимального маршрута перевозки грузов по городу можно принять, что вершинами орграфа являются перекрестки улиц, ребрами – отрезки улиц между перекрестками, весами – расстояние между вершинами.

Каждые две вершины могут соединять две дуги- туда и обратно, имеющие разный вес. Действительно, если пункт А расположен на горе, а пункт Б – в низине, то время на проезд из А в Б очевидно меньше времени на проезд из Б в А. Каждая вершина может быть посещена не более одного раза.

Взвешенный орграф может быть задан как графически, так и с помощью матрицы размерностью - количество вершин графа. Число 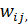, нахождение в ячейке (, является весом ребра, соединяющего i -ю и j -ю вершины. Если ячейка 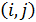пуста, то это означает, что из i -й верщины в j -ю перемещение невозможно.

Оптимизационные задачи на графах, возникающие при подготовке управленческих решений, весьма многообразны.

 

Методические указания

Рассмотрим методику поиска кратчайшего пути на примере. Пусть имеется орграф, представленный на рисунке 1.

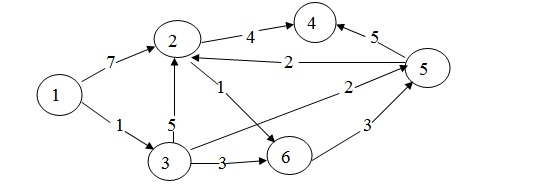
Рис. 1. Исходные данные к задаче в виде взвешенного орграфа

 

Приведенный граф может быть записан также в виде таблицы:

j i	Номера вершин
Номера вершин

 

Пусть необходимо найти кратчайший путь между вершинами 1 и 4.

Введем обозначение: С(Т) – длина кратчайшего пути из вершины 1 в вершину Т.

Оставленная задача состоит в вычислении С(4) и указании пути с минимальной стоимостью проезда.

Рассмотрим подробнее взвешенный орграф, представленный на рисунке 1.

В вершину 4 можно попасть либо из вершины 2, пройдя путь, равный 4,либо из вершины 5, пройдя путь, равный 5. Поэтому справедливо соотношение

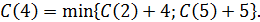
Таким образом, проведена реструктуризация (упрощение) задачи – нахождение С(4) сведено к нахождению С(2) и С(5).

В вершину 5 можно попасть либо из вершины 3, пройдя путь, равный 2, либо из вершины 6, пройдя путь, равный 3. Поэтому справедливо соотношение .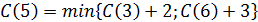

В вершину 3 входит только одна стрелка, как раз из вершины 1, и около этой стрелки стоит ее длина, равная 1, следовательно С(3)=1.

Поэтому .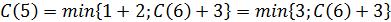

Поскольку очевидно, что С(6) – положительное число, то из последнего соотношения вытекает, что С(5)=3, то есть вычислять значение С(6) не имеет смысла, поскольку выражение С(6)+3 всегда будет больше 3.

В вершину 2 можно попасть либо из вершины 1, пройдя путь, равный 7, либо из вершины 3, пройдя путь, равный 5, либо из вершины 5, пройдя путь, равный 2. Поэтому справедливо соотношение

.

Очевидно, что С(1)=0. Нам известно, что С(3)=1, С(5)=3.

Поэтому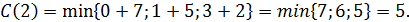

Теперь мы можем найти С(4):

Таким образом, длина кратчайшего пути равна 8. Из последнего соотношения ясно, что в вершину 4 надо идти через вершину 5. Возвращаясь к вычислению С(5), видим, что в вершину 5 надо идти через вершину 3. А в вершину 3 можно попасть только из вершины 1. Итак, кратчайший путь таков: 1→3→5→4.

Задача о кратчайшем пути для исходных данных полностью решена.

Варианты заданий

Найти кратчайший путь между вершинами 1 и 4 во взвешенном орграфе, заданном таблицей.

Вариант №1

j i	Номера вершин
Номера вершин

 

Вариант №2

j i	Номера вершин
Номера вершин

 

Вариант №3

j i	Номера вершин
Номера вершин

 

Вариант №4

j i	Номера вершин
Номера вершин

Вариант №5

j i	Номера вершин
Номера вершин

 

Вариант №6

j i	Номера вершин
Номера вершин

 

Вариант №7

j i	Номера вершин
Номера вершин

 

Вариант №8

j i	Номера вершин
Номера вершин

 

 

Вариант №9

j i	Номера вершин
Номера вершин

 

Вариант №10

j i	Номера вершин
Номера вершин

 

Контрольное задание 3

Методы обработки экспертных оценок

Цель работы

Изучение методов экспертной оценки эффективности принимаемых решений.

 

Краткие теоретические сведения

В настоящее время распространены экспертные, маркетинговые, ква-лиметрические, социологические и иные опросы, в которых опрашиваемых просят выставить баллы объектам, изделиям, технологическим процессам, предприятиям, проектам, заявкам на выполнение научно-исследовательских работ, идеям, проблемам, программам, политикам и т.п., а затем рассчиты­вают средние баллы и рассматривают их как интегральные оценки, выстав­ленные коллективом опрошенных. Какими формулами пользоваться для вы­числения средних величин?

Целесообразно использовать одновременно два метода: метод средних арифметических рангов (баллов) и метод медианных рангов. Такая рекомен­дация находится в согласии с концепцией устойчивости, рекомендующей ис­пользовать различные методы для обработки одних и тех же данных с целью выделить выводы, получаемые одновременно при всех методах. Такие выво­ды, видимо, соответствуют действительности, в то время как заключения, меняющиеся от метода к методу, зависят от субъективизма исследователя, выбирающего метод обработки исходных экспертных оценок.

Методические указания

Для демонстрации упомянутых методов обработки экспертных оценок рассмотрим пример сравнения восьми проектов. Экспертному совету, в со­став которого входит 12 специалистов, было представлено восемь проектов по развитию новых направлений бизнеса. Задача экспертов заключается в определении наиболее перспективного проекта для последующего выделения под него кредита на льготных условиях.

Проекты обозначены восемью первыми буквами латинского алфавита А,...,Н. В таблице 1 приведены ранги восьми проектов, присвоенные им каж­дым из 12 экспертов в соответствии с их представлением о целесообразности выделения кредита авторам проекта. При этом эксперт присваивает ранг 1 самому лучшему проекту, который обязательно надо реализовать. Ранг 2 по­лучает от эксперта второй по привлекательности проект,... наконец, ранг 8 -наиболее сомнительный проект, который стоит реализовывать в последнюю очередь. Анализируя результаты работы экспертов (то есть табл. 1), руководители финансовых структур были вынуждены констатировать, что полного согласия между экспертами нет, а потому данные, приведенные в таблице 1, следует подвергнуть более тщательному математическому анализу.

 

 

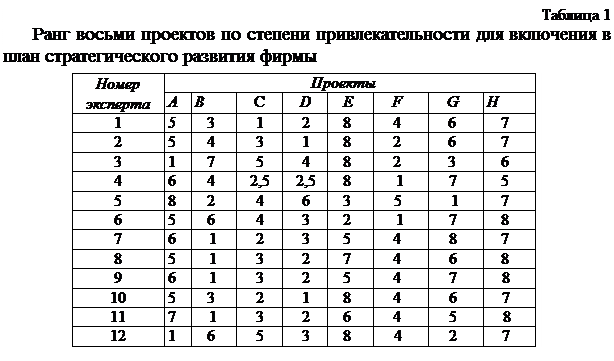
Примечание. Эксперт № 4 считает, что проекты С и D равноценны, но усту­пают лишь одному проекту - F. Поэтому проекты С и D должны были бы стоять на втором и третьем местах и получить баллы 2 и 3 соответственно. Но поскольку они равноценны, то получают средний балл (2+3)/ 2 = 5/2 = 2,5.

Сначала был применен метод средних арифметических рангов. Для этого была подсчитана сумма рангов, присвоенных проектам. Затем эта сум­ма была разделена на число экспертов, в результате рассчитан средний арифметический ранг (именно эта операция дала название методу). По сред­ним рангам строится итоговая ранжировка (в другой терминологии - упоря­дочение), исходя из принципа: чем меньше средний ранг, тем лучше проект.

Наименьший средний ранг, равный 2,625, у проекта D, следовательно, в итоговой ранжировке он получает ранг 1. Следующая по величине сумма, равная 3,125, у проекта С, и он получает итоговый ранг 2. Проекты В и F имеют одинаковые суммы (равные 3,25), значит, с точки зрения экспертов, они равноценны (при рассматриваемом способе оценки мнений экспертов), а потому они должны бы стоять на 3 и 4-м местах и получают средний балл (3+4) / 2 = 3,5. Дальнейшие результаты приведены в таблице 2.

Итак, ранжировка по суммам рангов (или, что то же самое, по средним арифметическим рангам) имеет вид:

 

D < С< {В, F} < А < G < Е < Н. (1)

Здесь запись типа «А<Б» означает, что проект А предшествует проекту Б (то есть проект А лучше проекта Б). Поскольку проекты В и F получили одинаковую сумму баллов, то по рассматриваемому методу они эквивалент­ны, а потому объединены в группу (в фигурных скобках). В терминологии математической статистики ранжировка (1) имеет одну связь

Далее был использован метод, в соответствии с которым проекты не­обходимо ранжировать по медианам рангов.

Рассмотрим вычисление медианы рангов проекта А. Для этого возьмем ответы экспертов, соответствующие проекту А из таблицы 1, и расположим их в порядке неубывания (проще было бы сказать - «в порядке возрастания», но поскольку некоторые ответы совпадают, то правильнее использовать термин «неубывание»). Получим последовательность: 1, 1, 5, 5, 5, 5, 5, 6, 6, 6, 7, 8. На центральных местах - шестом и седьмом - стоят 5 и 5. Следовательно, ме­диана равна 5.

Медианы совокупностей из 12 рангов, соответствующих определен­ным проектам, приведены в предпоследней строке таблицы 2. Итоговое упо­рядочение по методу медиан приведено в последней строке таблицы. Ранжи­ровка (то есть упорядочение - итоговое мнение комиссии экспертов) по ме­дианам имеет вид:

D < {С, B}<F<A<G<H<E. (2)

Поскольку проекты С и В имеют одинаковые медианы баллов, то по рассматриваемому методу ранжирования они эквивалентны, а потому объе­динены в группу (кластер), то есть с точки зрения математической статисти­ки ранжировка (2) имеет одну связь.

Сравнение ранжировок (1) и (2) показывает их близость (похожесть). Можно принять, что проекты С, В, F упорядочены как С < В < F, но из-за по­грешностей экспертных оценок в одном методе признаны равноценными проекты В и F (ранжировка (1)), а в другом - проекты С и В (ранжировка (2)). Существенным является только расхождение, касающееся упорядоче­ния проектов Н и Е: в ранжировке (1) Е < Н, а в ранжировке (2), наоборот, Н < Е. Однако эти проекты наименее привлекательные из восьми рассматри­ваемых, и при выборе наиболее привлекательных проектов для дальнейшего обсуждения и использования это расхождение несущественно.

Рассмотренный пример демонстрирует сходство и различие ранжиро­вок, полученных по методу средних арифметических рангов и по методу ме­диан, а также пользу их совместного применения.

Варианты заданий

Необходимо самостоятельно выбрать объекты для сравнения, смоделировать опрос экспертов, составить таблицу рангов по привлекательности некоторого товара/ресурса/проекта. Затем провести анализ представленных данных, используя метод средних арифметических рангов и метод медианных рангов. Дать обосно­ванное расчетами заключение о выборе наиболее перспективного товара/ресурса/проекта.

 

 

Учебное издание

⇐ Предыдущая1234

Поделиться:

Воспользуйтесь поиском по сайту: