 |
Равнобедренный треугольник.
|
|
|
|
Смежные и вертикальные углы.
1.1. Найти больший из смежных углов, если один из них на 380 меньше второго.
1.2. Найти больший из смежных углов, если один из них на 560 больше второго.
2.1. Найти меньший из смежных углов, если один из них в пять раз больше второго.
2.2. Найти меньший из смежных углов, если один из них в три раза меньше второго.
3.1. Найти больший из смежных углов, если их градусные меры относятся как 5:7.
3.2. Найти больший из смежных углов, если их градусные меры относятся как 7:8.
4. Найти величину большего из углов, образованных при пересечении двух прямых, если сумма двух из них равна 98 
.
5. Биссектриса угла и продолжение одной из его сторон образуют угол 124 . Найти исходный угол.
Треугольник.
6.1. Найти меньший угол треугольника, в котором один из углов на 300 больше второго и в три раза больше третьего.
6.2. Найти больший угол треугольника, в котором один из углов на 200 меньше второго и в два раза меньше третьего.
7. Найти средний угол треугольника, если градусные меры углов относятся как 3:5:7.
8.1. Два внешних угла треугольника равны 
и 
. Найти третий внешний угол.
8.2. Два внешних угла треугольника равны 
и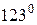 
. Найти третий внешний угол.
9. Могут ли длины сторон треугольника быть равными: а) 17 см., 36 см. и 19 см.; б) 83 см., 47 см. и 38 см.; в) 23 см., 28 см. и 52 см.?
10.1. Две стороны треугольника равны 7 см. и 11 см. Найти сумму целых значений, которые может принимать длина третьей стороны.
10.2. Две стороны треугольника равны 5 см. и 8 см. Найти сумму целых значений, которые может принимать длина третьей стороны.
11.1. В треугольнике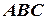 
=8 см., 
=10 см., 
=13 см., 
– середина , 
– середина . Найти периметр четырёхугольника 
.
11.2. В треугольнике 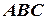=12 см., =15 см. =14 см., – середина , – середина . Найти периметр треугольника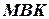 
.
|
|
|
12. Середины сторон треугольника, периметр которого 24 см., являются вершинами другого треугольника. Найти его периметр.
Прямоугольный треугольник.
13. В прямоугольном треугольнике угол между биссектрисой и высотой, проведёнными из вершины прямого угла, равен 15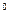 
. Найти меньший угол треугольника.
14. В прямоугольном треугольнике биссектрисы острого и прямого углов пересекаются под углом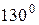 
. Найти меньший угол треугольника.
15.1.В прямоугольном треугольнике гипотенуза равна 5 см., а один из катетов 3 см. Найти периметр и площадь треугольника.
15.2. В прямоугольном треугольнике гипотенуза равна 13 см., а один из катетов 5 см. Найти периметр и площадь треугольника.
16.1. В прямоугольном треугольнике один из катетов на 8 см. меньше гипотенузы, а второй катет равен 12 см. Найти периметр и площадь треугольника.
16.2. В прямоугольном треугольнике один из катетов на 2 см. меньше гипотенузы, а второй катет равен 4 см. Найти периметр и площадь треугольника.
17.1. В прямоугольном треугольнике катеты относятся как 8:15, а гипотенуза равна 17 см. Найти периметр и площадь треугольника.
17.2. В прямоугольном треугольнике один из катетов относится к гипотенузе как 4:5, а второй равен 6 см. Найти периметр и площадь треугольника.
18.1.Найти площадь прямоугольного треугольника, если один из катетов равен 6 см., а медиана, проведённая к нему—5 см.
18.2.Найти площадь прямоугольного треугольника, если один из катетов равен 5 см., а медиана, проведённая к другому катету—13 см.
19. В прямоугольном треугольнике разность катетов равна 14 см., а гипотенуза равна 26 см. Найти периметр и площадь треугольника.
20. В прямоугольном треугольнике периметр равен 24 см., а гипотенуза относится к катету как 5:3. Найти площадь треугольника.
Равнобедренный треугольник.
21. Угол между высотами равнобедренного треугольника, проведёнными к боковым сторонам, равен 132 . Найти больший угол треугольника.
|
|
|
22. Угол между биссектрисами углов при основании равнобедренного треугольника равен 124 . Найти больший угол треугольника.
23.1. В треугольнике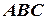 
, 
– биссектриса. Найти величины углов треугольника, если 
.
23.2. В треугольнике ,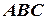 
– биссектриса. Найти величины углов треугольника, если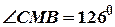 
.
24.1. Найти площадь равнобедренного треугольника (двумя способами), если его периметр 28 см., а основание на 8 см. меньше боковой стороны.
24.2.Найти площадь равнобедренного треугольника (двумя способами), если его периметр 22 см., а боковая сторона на 2 см. больше основания.
25. Найти площадь равнобедренного треугольника (двумя способами), если его периметр 50 см., а боковая сторона в два раза больше основания.
26.1. Найти периметр и площадь равнобедренного треугольника, если боковая сторона относится к основанию как 5:6, а высота, проведённая к основанию, равна 12 см.
26.2. Найти периметр и площадь равнобедренного треугольника, если основание равно 16 см., а боковая сторона на 2 см. больше высоты, проведённой к основанию.
27.1. Высота равнобедренного треугольника, проведённая к боковой стороне, равна 8 см и делит её на две части, одна из которых, прилежащая к вершине угла напротив основания, равна 6 см. Найти длину основания и площадь.
27.2. Высота равнобедренного треугольника делит боковую сторону на отрезки длиной 4 см и 16 см, считая от вершины угла при основании. Найти длину основания и площадь.
28.1. Угол при вершине равнобедренного треугольника 600, а его площадь – 4 
см2. Найти длину боковой стороны.
28.2. Угол при вершине равнобедренного треугольника 300, а его площадь – 9 см2. Найти длину боковой стороны.
29.1. Высота правильного треугольника равна 12 
см. Найти его периметр.
29.2. Периметр правильного треугольника равен 48 см. Найти длину высоты.
Подобные треугольники.
30.1. Стороны двух треугольников равны 5 см., 8 см., 9 см. и 15 см., 24 см., 27 см. соответственно. Подобны ли эти треугольники?
30.2. Стороны двух треугольников равны 8 см., 6 см., 12 см. и 4 см., 3 см., 6 см. соответственно. Подобны ли эти треугольники?
31.1. Стороны треугольника равны 7 см., 8 см. и 9 см. Найти длину большей стороны подобного треугольника, если его периметр равен 12 см.
|
|
|
31.2. Стороны треугольника равны 5 см., 6 см. и 7 см. Найти меньшую сторону подобного треугольника, если его периметр равен 72 см.
32.1. Стороны двух правильных треугольников относятся как 4:7, площадь большего 98 см 
. Найти площадь меньшего треугольника.
32.2. Стороны двух правильных треугольников относятся как 3:5, площадь меньшего 36 см . Найти площадь большего треугольника.
|
|
|
