 |
Теоремы косинусов и синусов.
|
|
|
|
33.1. Из вершины угла треугольника проведена высота длиной  см., которая делит этот угол на углы
см., которая делит этот угол на углы  и
и  . Найти стороны треугольника.
. Найти стороны треугольника.
33.2. В треугольнике 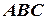 провели высоту
провели высоту 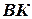 . Найти
. Найти  , если
, если  см.,
см., 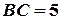 см.,
см., 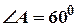 .
.
34.1. Найти сторону  треугольника
треугольника 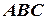 , если
, если 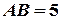 см.,
см.,  см.,
см.,  .
.
34.2. Найти сторону  треугольника
треугольника 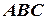 , если
, если  см.,
см.,  см.,
см.,  .
.
35.1. Две стороны треугольника равны 3 см. и 7 см., а угол напротив большей из них равен  . Найти площадь треугольника.
. Найти площадь треугольника.
35.2. Две стороны треугольника равны 3 см. и 7 см., а угол напротив большей из них равен  . Найти площадь треугольника.
. Найти площадь треугольника.
36. Одна из сторон треугольника равна 7 см., а вторая на 5 см. больше третьей и образует с ней угол 60 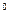 . Найти периметр треугольника.
. Найти периметр треугольника.
37. Одна из сторон треугольника равна 35 см., а две другие относятся как 3:8 и образуют угол  . Найти периметр треугольника.
. Найти периметр треугольника.
38.1. В треугольнике 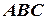
 см.,
см., 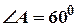 ,
, 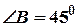 . Найти длину
. Найти длину  .
.
38.2. В треугольнике 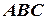
 см.,
см.,  ,
,  . Найти длину
. Найти длину  .
.
39.1. В треугольнике 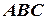
 см.,
см., 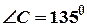 ,
,  . Найти длину
. Найти длину  .
.
39.2. В треугольнике 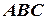
 см.,
см.,  ,
,  . Найти длину
. Найти длину  .
.
Площадь треугольника.
40. Найти площадь равнобедренного треугольника, если его основание равно 6 см., а боковая сторона – 5 см. (двумя способами)
41.1. Стороны треугольника равны 6 см, 25 см и 29 см. Найти длину высоты, проведённой к меньшей стороне.
41.2. Стороны треугольника равны 13 см, 14 см и 15 см. Найти длину высоты, проведённой к средней стороне.
Прямоугольник.
42.1. Диагональ квадрата равна 6 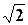 см. Найти его периметр и площадь.
см. Найти его периметр и площадь.
42.2. Периметр квадрата равен 24 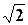 см. Найти площадь квадрата.
см. Найти площадь квадрата.
42.3. Площадь квадрата равна 18 см.2. Найти периметр квадрата.
43.1. В прямоугольнике диагональ образует с большей стороной угол 320. Найти угол между диагоналями, лежащий напротив меньшей стороны.
43.2. В прямоугольнике диагональ образует с меньшей стороной угол 460. Найти угол между диагоналями, лежащий напротив большей стороны.
|
|
|
44.1. Найти угол между меньшей стороной и диагональю прямоугольника, если он на 300 меньше меньшего угла между диагоналями.
44.2. Найти угол между большей стороной и диагональю прямоугольника, если он на 600 меньше большего угла между диагоналями.
45. Угол между диагоналями прямоугольника равен  . Найти длины меньшей стороны и диагонали, если большая сторона равна
. Найти длины меньшей стороны и диагонали, если большая сторона равна  см.
см.
46.1. Найти площадь прямоугольника, если его сторона равна 8 см. и образует с диагональю угол 300.
46.2. Найти площадь прямоугольника, если его диагональ равна  см. и образует со стороной угол 600.
см. и образует со стороной угол 600.
47. Найти периметр прямоугольника, если его площадь равна 21 см.2 и одна из сторон на 4 см. больше другой.
48. Найти периметр прямоугольника, если его площадь равна 144 см.2 и одна из сторон в 8 раз больше другой.
49. Найти периметр и площадь прямоугольника, если разность его сторон 4 см., а диагональ – 20 см.
50. Периметр прямоугольника равен 56 см. Найти длину диагонали, если разность сторон равна 4 см.
Параллелограмм.
51.1. Найти площадь параллелограмма, если его периметр равен 22 см, одна из сторон на 3 см. больше второй, а тупой угол равен 1500.
51.1. Найти площадь параллелограмма, если его периметр равен 28 см, стороны относятся как  , а острый угол равен 300.
, а острый угол равен 300.
52.1. Найти площадь параллелограмма, если его стороны равны 5 см. и 2  см., а один из углов в два раза больше второго.
см., а один из углов в два раза больше второго.
52.2. Найти площадь параллелограмма, если его стороны равны 3 см. и 5 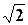 см., а сумма двух углов 900.
см., а сумма двух углов 900.
53.1. Площадь параллелограмма равна 45 см2, а его высота на 4 см. меньше стороны, к которой проведена. Найти данную сторону.
53.2. Площадь параллелограмма равна 112 см2, а его высота в 7 раз меньше стороны, к которой проведена. Найти данную сторону.
54. Два угла параллелограмма относятся как 3:7. Найти угол между высотами, проведёнными из вершины тупого угла.
|
|
|
55.1. Найти площадь параллелограмма, если биссектриса тупого угла делит его сторону на части длиной 3 см. и 5 см., считая от вершины острого угла, который равен  .
.
55.2. Найти площадь параллелограмма, если биссектриса острого угла делит его сторону на части длиной 6 см. и 2 см., считая от вершины тупого угла, который равен  .
.
56.1. Найти площадь параллелограмма, если его диагонали равны 16 см. и 20 см., и одна из них перпендикулярна стороне.
56.2. Найти площадь параллелограмма, если его стороны равны 9 см. и 15 см., а одна из диагоналей перпендикулярна стороне.
Ромб.
57.1. Угол между стороной и меньшей диагональю ромба равен 520. Найти острый угол ромба.
57.2. Угол между стороной и большей диагональю ромба равен 280. Найти тупой угол ромба.
58. Найти острый угол ромба, если высоты, проведённые из вершины тупого угла, образуют угол 480.
59. Найти тупой угол ромба, если высота, проведённая из вершины тупого угла, делит его сторону пополам.
60.1. Угол между стороной и большей диагональю ромба равен 300, а сама диагональ – 10  см. Найти периметр и площадь ромба.
см. Найти периметр и площадь ромба.
60.2. Угол между стороной и меньшей диагональю ромба равен 600, а сама диагональ – 6 см. Найти периметр и площадь ромба.
61.1. Диагонали ромба равны 6 см. и 8 см. Найти периметр и площадь ромба.
61.2. Диагонали ромба равны 10 см. и 24 см. Найти периметр и площадь ромба.
62. Сторона ромба 15 см., а одна из диагоналей – 18 см. Найти длину второй диагонали.
63.1. Найти периметр ромба, если его площадь 120 см2, а диагонали относятся как 5:12.
63.2. Найти периметр ромба, если его площадь 96 см2, а диагонали относятся как 3:4.
64. Найти площадь ромба, если его сторона равна 5 см., а сумма диагоналей – 14 см.
65.1. Угол между стороной ромба и высотой, проведённой из вершины тупого угла, равен 600, а сама высота – 5 см. Найти периметр и площадь ромба.
65.2. Угол между стороной ромба и высотой, проведённой из вершины тупого угла, равен 600, а сама сторона – 8 см. Найти периметр и площадь ромба.
66. Сторона ромба равна 25 см., а высота – 24 см. Найти диагонали ромба.
Трапеция.
67.1. В трапеции одно из оснований на 6 см. меньше другого, а длина средней линии равна 19 см. Найти длину меньшего основания.
67.2. В трапеции одно из оснований в три раза больше другого, а длина средней линии равна 4 см. Найти длину большего основания.
|
|
|
68. Средняя линия трапеции в два раза больше меньшего основания и на 8 см. меньше большего. Найти её длину.
69.1. В трапеции  продолжение боковых сторон
продолжение боковых сторон  и
и  пересекаются в точке
пересекаются в точке 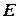 . Найти
. Найти  , если
, если 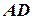 =12см.,
=12см.,  =15 см. и
=15 см. и  =5 см.
=5 см.
69.2. В трапеции  продолжение боковых сторон
продолжение боковых сторон  и
и  пересекаются в точке
пересекаются в точке  . Найти
. Найти  , если
, если 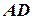 =26 см.,
=26 см.,  =9 см. и
=9 см. и  =4 см.
=4 см.
70.1. В трапеции  продолжение боковых сторон
продолжение боковых сторон  и
и  пересекаются в точке
пересекаются в точке  . Найти
. Найти  , если
, если  =10 см. и
=10 см. и  .
.
70.2. В трапеции  продолжение боковых сторон
продолжение боковых сторон  и
и  пересекаются в точке
пересекаются в точке 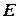 . Найти
. Найти  , если
, если  =36 см. и
=36 см. и  .
.
71. В трапеции  (
( )
)  – точка пересечения диагоналей.
– точка пересечения диагоналей.  , средняя линия равна 7 см. Найти меньшее основание.
, средняя линия равна 7 см. Найти меньшее основание.
72. Точка пересечения диагоналей трапеции делит одну из диагоналей трапеции на отрезки 7 см. и 11 см. Найти большее основание трапеции, если разность оснований равна 16 см.
73.1. Диагональ трапеции делит среднюю линию на отрезки, один из которых на 5 см. больше другого. Найти большее основание, если меньшее равно 6 см.
73.2. Диагональ трапеции делит среднюю линию на отрезки, один из которых в два раза больше другого. Найти меньшее основание, если большее равно 10 см.
74.1. Диагональ равнобокой трапеции образует с основанием угол 320, а боковая сторона равна меньшему основанию. Найти меньший угол трапеции.
74.2. Диагональ равнобокой трапеции равна большему основанию и образует с ним угол 380. Найти больший угол трапеции.
75.1. В равнобокой трапеции угол между диагоналями 800, а боковая сторона равна большему основанию. Найти больший угол трапеции.
75.2. В равнобокой трапеции угол между диагоналями 1100, а боковая сторона равна меньшему основанию. Найти меньший угол трапеции.
76. В равнобокой трапеции диагональ перпендикулярна боковой стороне и является биссектрисой острого угла. Найти меньший угол трапеции.
77. Основания и боковая сторона равнобокой трапеции равны 3 см., 17 см. и 25 см. соответственно. Найти длину диагонали.
78. Основания равнобокой трапеции равны 6 см. и 16 см, а боковая сторона образует с большим основанием угол 600. Найти длину диагонали.
79. Найти площадь равнобокой трапеции, если основания 18 см. и 36 см., диагональ – 45 см.
|
|
|
80.1. Найти площадь равнобокой трапеции, если большее основание 9  см., боковая сторона 8 см., тупой угол 1350.
см., боковая сторона 8 см., тупой угол 1350.
80.2. Найти площадь равнобокой трапеции, если меньшее основание 10 см., боковая сторона 6 см., тупой угол 1200.
81.1. Основания равнобокой трапеции равны 12 см. и 20 см., а диагональ является биссектрисой тупого угла. Найти площадь трапеции.
81.2. Основания равнобокой трапеции равны 12 см. и 18 см., а диагональ является биссектрисой острого угла. Найти площадь трапеции.
82. Найти острый угол прямоугольной трапеции, если её тупой угол в пять раз больше острого.
83. Боковые стороны и большая диагональ прямоугольной трапеции равны 12 см,.15 см. и 20 см. соответственно. Найти длины оснований.
84. Высота и боковая сторона прямоугольной трапеции равны 12 см. и 15 см. Найти периметр трапеции, если диагональ делит острый угол пополам.
85.1. Меньшее основание прямоугольной трапеции равно 12 см., а меньшая боковая сторона – 4  см. Найти площадь трапеции, если один из её углов равен 1200.
см. Найти площадь трапеции, если один из её углов равен 1200.
85.2. Меньшее основание прямоугольной трапеции равно 12 см., а высота – 3  см. Найти площадь трапеции, если один из её углов равен 1500.
см. Найти площадь трапеции, если один из её углов равен 1500.
86. Найти площадь прямоугольной трапеции, если меньшее основание 5  см., большая боковая сторона 18 см., тупой угол 1500.
см., большая боковая сторона 18 см., тупой угол 1500.
Окружность.
87.1. Длина окружности равна  см. Найти площадь соответствующего круга.
см. Найти площадь соответствующего круга.
87.2. Площадь круга равна  см
см  . Найти длину соответствующей окружности.
. Найти длину соответствующей окружности.
88. Диаметр окружности равен 8 см. Найти длину окружности и площадь круга.
89. Радиусы двух окружностей равны 7 см. и 11 см. Найти расстояние между их центрами, если окружности касаются (рассмотреть два варианта).
90.1. Найти площадь кольца между двумя концентрическими окружностями радиусами 4 см. и 6 см.
90.2. Найти площадь кольца между двумя концентрическими окружностями радиусами 5 см. и 8 см.
91.1. Точки  и
и  лежат на окружности по одну сторону от хорды
лежат на окружности по одну сторону от хорды  . Найти
. Найти  , если
, если  .
.
91.2. Точки  и
и  лежат на окружности по разные стороны от хорды
лежат на окружности по разные стороны от хорды  . Найти
. Найти  , если
, если  .
.
92.1. Из точки на окружности проведены две хорды. Найти угол между ними, если одна из них стягивает дугу  , а другая –
, а другая –  .
.
92.2. Из точки на окружности проведены две хорды, угол между которыми  . Одна из хорд стягивает дугу
. Одна из хорд стягивает дугу  . Найти дугу, стягиваемую второй хордой.
. Найти дугу, стягиваемую второй хордой.
93. Радиусы двух окружностей равны 3 см. 8 см., а расстояние между их центрами – 13 см. Найти длину их общей внешней касательной.
94.1. Хорда стягивает дугу  . Найти острый угол между этой хордой и касательной к окружности, проведённой через конец хорды.
. Найти острый угол между этой хордой и касательной к окружности, проведённой через конец хорды.
94.2. Тупой угол между хордой и касательной, проведённой через её конец, равен 1300. Найти градусную меру дуги, которую стягивает эта хорда.
|
|
|
95.1. Длина дуги окружности  см., а её градусная мера – 180. Найти радиус окружности.
см., а её градусная мера – 180. Найти радиус окружности.
95.2. Длина дуги окружности  см., а её градусная мера – 240. Найти радиус окружности.
см., а её градусная мера – 240. Найти радиус окружности.
96.1. Длина дуги окружности радиусом 30 см. равна  . Найти её градусную меру.
. Найти её градусную меру.
96.2. Длина дуги окружности радиусом 20 см. равна  . Найти её градусную меру.
. Найти её градусную меру.
97.1. Найти радиус круга, если площадь сектора, образованного центральным углом 1080, равна 7,5  см2.
см2.
97.2. Найти радиус круга, если площадь сектора, образованного центральным углом 720, равна 45  см2.
см2.
98. Найти площадь сектора круга радиусом 5 см., если соответствующий центральный угол равен 1500.
99.1. Радиус окружности, описанной около равностороннего треугольника, равен  см. Найти периметр треугольника.
см. Найти периметр треугольника.
99.2. Периметр равностороннего треугольника равен  см. Найти радиус окружности, описанной около треугольника.
см. Найти радиус окружности, описанной около треугольника.
100.1. Периметр правильного треугольника равен  см. Найти радиус окружности, вписанной в треугольник.
см. Найти радиус окружности, вписанной в треугольник.
100.2. Радиус окружности, вписанной в правильный треугольник, равен 6  см. Найти периметр треугольника.
см. Найти периметр треугольника.
101.1. Найти площадь круга, вписанного в треугольник со сторонами 4 см., 13 см. и 15 см.
101.2. Найти площадь круга описанного около треугольника со сторонами 13 см., 14 см. и 15 см.
102.1. Радиус окружности, описанной около квадрата, равен  см. Найти радиус окружности, вписанной в квадрат.
см. Найти радиус окружности, вписанной в квадрат.
102.2. Радиус окружности, вписанной в квадрат, равен 8 см. Найти радиус окружности, описанной около квадрата.
103. Радиус окружности, описанной около прямоугольника, равен 5 см., а стороны относятся как 3:4. Найти периметр и площадь прямоугольника.
Многоугольники.
104.1. Найти меньший угол выпуклого семиугольника, если его углы относятся как 4:5:6:7:7:8:8.
104.2. Найти меньший угол выпуклого девятиугольника, если его углы относятся как 5:6:7:8:8:9:9:9:9.
105. Найти меньший угол выпуклого пятиугольника, если один из углов 115 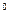 , второй, третий и четвёртый относятся как 7:5:3, а пятый равен полуразности второго и четвёртого.
, второй, третий и четвёртый относятся как 7:5:3, а пятый равен полуразности второго и четвёртого.
106.1. Найти количество сторон выпуклого многоугольника, если сумма внутренних углов на 540 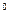 больше суммы внешних.
больше суммы внешних.
106.2. Найти количество сторон выпуклого многоугольника, если сумма внутренних углов в два раза больше суммы внешних.
107.1. Найти количество сторон правильного многоугольника, если а) внутренний угол равен 168 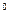 ; б) внешний угол равен 18
; б) внешний угол равен 18 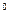 ; в) центральный угол равен 15
; в) центральный угол равен 15 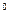 .
.
107.2. Найти количество сторон правильного многоугольника, если а) внутренний угол равен 172 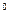 ; б) внешний угол равен 24
; б) внешний угол равен 24 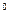 ; в) центральный угол равен 24
; в) центральный угол равен 24 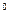 .
.
108. Найти количество сторон правильного многоугольника, если сумма внешних углов вместе с одним из внутренних равна 5320.
Ответы. 1.1. 109  ; 1.2. 118
; 1.2. 118  ; 2.1. 30
; 2.1. 30  ; 2.2. 45
; 2.2. 45  ; 3.1. 30
; 3.1. 30  ; 3.2. 12
; 3.2. 12  ; 4. а) 131
; 4. а) 131  ; б) 119
; б) 119 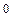 ; 5. 112
; 5. 112  ; 6.1. 30
; 6.1. 30  ; 6.2. 80
; 6.2. 80  ; 7. 60
; 7. 60  ; 8.1. 134
; 8.1. 134  ; 8.2. 130
; 8.2. 130  ; 9. а) нет; б) да; в) нет; 10.1. 143 см.; 10.2. 72 см.; 11.1. 28,5 см.; 11.2. 20,5 см.; 12. 12 см.; 13. 300; 14. 100; 15.1. 12 см. и 6 см.2; 15.2. 30 см. и 30 см.2; 16.1. 30 см. и 30 см.2; 16.2. 12 см. и 6 см.2; 17.1. 40 см. и 60 см.2; 17.2. 24 см. и 24 см.2; 18.1. 12 см.2; 18.2. 60 см.2; 19. 60 см. и 120 см.2; 20. 24 см.2; 21. 660; 22. 680; 23.1. 240, 780 и 780; 23.2. 120, 840 и 840; 24.1. 4
; 9. а) нет; б) да; в) нет; 10.1. 143 см.; 10.2. 72 см.; 11.1. 28,5 см.; 11.2. 20,5 см.; 12. 12 см.; 13. 300; 14. 100; 15.1. 12 см. и 6 см.2; 15.2. 30 см. и 30 см.2; 16.1. 30 см. и 30 см.2; 16.2. 12 см. и 6 см.2; 17.1. 40 см. и 60 см.2; 17.2. 24 см. и 24 см.2; 18.1. 12 см.2; 18.2. 60 см.2; 19. 60 см. и 120 см.2; 20. 24 см.2; 21. 660; 22. 680; 23.1. 240, 780 и 780; 23.2. 120, 840 и 840; 24.1. 4  см.2; 24.2. 3
см.2; 24.2. 3  см.2; 25. 12,5
см.2; 25. 12,5  см.2; 26.1. 48 см. и 108 см.2; 26.2. 50 см. и 120 см.2; 27.1. 4
см.2; 26.1. 48 см. и 108 см.2; 26.2. 50 см. и 120 см.2; 27.1. 4  см. и 40 см2; 27.2. 4
см. и 40 см2; 27.2. 4  см. и 120 см2; 28.1. 4 см.; 28.2. 6 см.; 29.1. 72 см.; 29.2. 24 см.; 30.1. да; 30.2. да; 31.1. 4,5 см.; 31.2. 20 см.; 32.1. 32 см2; 32.2. 100 см2; 33.1. 8
см. и 120 см2; 28.1. 4 см.; 28.2. 6 см.; 29.1. 72 см.; 29.2. 24 см.; 30.1. да; 30.2. да; 31.1. 4,5 см.; 31.2. 20 см.; 32.1. 32 см2; 32.2. 100 см2; 33.1. 8  см., 12
см., 12 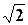 см. и (4
см. и (4  +12) см.; 33.2. 4 см.; 34.1.
+12) см.; 33.2. 4 см.; 34.1.  см.; 34.2.
см.; 34.2.  см.; 35.1. 15
см.; 35.1. 15  /4 см2.; 35.2. 6
/4 см2.; 35.2. 6  см2.; 36. 18 см.; 37. 90 см.; 38.1. 5
см2.; 36. 18 см.; 37. 90 см.; 38.1. 5 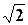 см.; 38.2. 4 см.; 39.1. 3 см.; 39.2. 6
см.; 38.2. 4 см.; 39.1. 3 см.; 39.2. 6 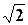 см.; 40. 12 см2; 41.1. 20 см.; 41.2. 12 см.; 42.1. 24 см. и 36 см2; 42.2. 72 см2; 42.3. 12
см.; 40. 12 см2; 41.1. 20 см.; 41.2. 12 см.; 42.1. 24 см. и 36 см2; 42.2. 72 см2; 42.3. 12 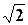 см.; 43.1. 640; 43.2. 920; 44.1. 500; 44.2. 400; 45. 12 см. и 24 см.; 46.1. 64/
см.; 43.1. 640; 43.2. 920; 44.1. 500; 44.2. 400; 45. 12 см. и 24 см.; 46.1. 64/  см2; 46.2. 108
см2; 46.2. 108  см2; 47. 20 см.; 48. 54
см2; 47. 20 см.; 48. 54 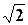 см.; 49. 56 см. и 192 см2; 50. 20 см.; 51.1. 14 см2; 51.2. 20 см2; 52.1. 15 см2; 52.2. 15 см2; 53.1. 9 см.; 53.2. 28 см.; 54. 540; 55.1. 12
см.; 49. 56 см. и 192 см2; 50. 20 см.; 51.1. 14 см2; 51.2. 20 см2; 52.1. 15 см2; 52.2. 15 см2; 53.1. 9 см.; 53.2. 28 см.; 54. 540; 55.1. 12  см2; 55.2. 24 см2; 56.1. 96 см2; 56.2. 108 см2; 57.1. 760; 57.2. 1240; 58. 480; 59. 1200; 60.1. 40 см. и 50
см2; 55.2. 24 см2; 56.1. 96 см2; 56.2. 108 см2; 57.1. 760; 57.2. 1240; 58. 480; 59. 1200; 60.1. 40 см. и 50  см2; 60.2. 24 см. и 18
см2; 60.2. 24 см. и 18  см2; 61.1. 20 см. и 24 см2; 61.2. 52 см. и 120 см2; 62. 24 см.; 63.1. 52 см.; 63.2. 40 см.; 64. 24 см2; 65.1. 40 см. и 50 см2; 65.2. 32 см. и 32 см2; 66. 30 см. и 40 см.; 67.1. 16 см.; 67.2. 6 см.; 68. 16 см.; 69.1. 4 см.; 69.2. 18 см.; 70.1. 6 см.; 70.2. 15 см.; 71. 6 см.; 72. 44 см.; 73.1. 16 см.; 73.2. 5 см.; 74.1. 640; 74.2. 1090; 75.1. 1000; 75.2. 700; 76. 600; 77. 26 см.; 78. 14 см.; 79. 972 см2; 80.1. 40 см2; 80.2. 39
см2; 61.1. 20 см. и 24 см2; 61.2. 52 см. и 120 см2; 62. 24 см.; 63.1. 52 см.; 63.2. 40 см.; 64. 24 см2; 65.1. 40 см. и 50 см2; 65.2. 32 см. и 32 см2; 66. 30 см. и 40 см.; 67.1. 16 см.; 67.2. 6 см.; 68. 16 см.; 69.1. 4 см.; 69.2. 18 см.; 70.1. 6 см.; 70.2. 15 см.; 71. 6 см.; 72. 44 см.; 73.1. 16 см.; 73.2. 5 см.; 74.1. 640; 74.2. 1090; 75.1. 1000; 75.2. 700; 76. 600; 77. 26 см.; 78. 14 см.; 79. 972 см2; 80.1. 40 см2; 80.2. 39  см2; 81.1. 128
см2; 81.1. 128 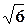 см2; 81.2. 45
см2; 81.2. 45  см2; 82. 300; 83. 50 см.; 84. 66 см.; 85.1. 56
см2; 82. 300; 83. 50 см.; 84. 66 см.; 85.1. 56  см2; 85.2. 58,5
см2; 85.2. 58,5  см2; 86. 85,5
см2; 86. 85,5  см2; 87.1. 36
см2; 87.1. 36  см2; 87.2. 10
см2; 87.2. 10  см.; 88. 8
см.; 88. 8  см. и 16
см. и 16  см2; 89. 18 см. или 4 см.; 90.1. 20
см2; 89. 18 см. или 4 см.; 90.1. 20  см2; 90.2. 39
см2; 90.2. 39  см2; 91.1. 420; 91.2. 1020; 92.1. 1000; 92.2. 1000; 93. 12 см.; 94.1. 400; 94.2. 1000; 95.1. 150 см.; 95.2. 60 см.; 96.1. 120; 96.2. 450; 97.1. 5 см.; 97.2. 15 см.; 98. 125
см2; 91.1. 420; 91.2. 1020; 92.1. 1000; 92.2. 1000; 93. 12 см.; 94.1. 400; 94.2. 1000; 95.1. 150 см.; 95.2. 60 см.; 96.1. 120; 96.2. 450; 97.1. 5 см.; 97.2. 15 см.; 98. 125  /12 см2; 99.1. 54 см.; 99.2. 8 см.; 100.1. 4 см.; 100.2. 108 см.; 101.1. 2,25
/12 см2; 99.1. 54 см.; 99.2. 8 см.; 100.1. 4 см.; 100.2. 108 см.; 101.1. 2,25  см2; 101.2. (65/8)2
см2; 101.2. (65/8)2  см2; 102.1. 5 см.; 102.2. 8
см2; 102.1. 5 см.; 102.2. 8 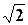 см.; 103. 28 см. и 48 см2; 104.1. 800; 104.2. 900; 105. 500; 106.1. 7; 106.2. 6; 107.1. 300, 200, 240; 107.2. 450, 150, 150; 108. 45.
см.; 103. 28 см. и 48 см2; 104.1. 800; 104.2. 900; 105. 500; 106.1. 7; 106.2. 6; 107.1. 300, 200, 240; 107.2. 450, 150, 150; 108. 45.
|
|
|


