Задачи вступительных экзаменов

Задача 6. Кубик плотности ρ находится в равновесии под наклонной стенкой (угол наклона α) в жидкости плотности ρ_ж >ρ и удерживается невесомой пружиной. Между стенкой и кубиком - тонкий слой жидкости. До какой величи­ны растянута пружина, если в отсут­ствии жидкости подвешенный на нее кубик растягивает ее до величины l, а длина ненагруженной пру­жины l₀?

Краткое решение. Растяжение пружины пропорционально нагрузке. Тонкий слой жидкости передает давление - в результате можно находить выталкивающую силу обычным путем 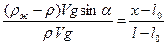; х = l ₀+(l - l ₀)(ρ_ж/ρ-1)sin α.

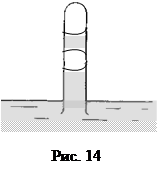Задача 7. Посередине барометри­ческой трубки имеется стол­бик воздуха. При температуре t₀ =0°С длина столбика равна l₀ = 10 см. Какой станет дли­на столбика при t = 20° С?

Решение. Давление в столбике воздуха равно весу столбика жидкости над воздухом, деленному на площадь сечения трубки. При изменении температуры изменится и высота столбика жид­кости, и его плотность. Но масса останется прежней. Прежним останется и вес столбика, а, следовательно, не изменится и давление воздуха. Поэтому отношение объемов воздушного столбика при температурах Т =293 К и Т₀ = 273 К равно отношению температур, и следовательно, 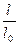= 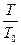. Отсюда l = l₀ 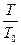≈ 10,7 см.

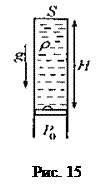Задача 8. Трубка, площадь сечения которой равна S, закрыта сверху и заполнена жидкостью плотности ρ на длину H. Внизу трубка перекрыта легким поршнем, к которому прилип пузырек воздуха объема V. Атмосферное давление Р_о. На какое расстояние х сдвинется поршень, если пузырек оторвется и всплывет вверх? Темпера­туру считать постоянной.

Решение. Вначале давление над поршнем атмосферное, а давление сверху меньше на величину ρgН. Давления определяются только равновесием поршня и жидкости и не зависят от присутствия пузырька. При всплывании давление в пузыре уменьшится от Р_о до (Р_о – ρgН), а объем возрастет до VР₀/(Р_о - ρgН). Изменение объема равно хS, где х - смещение поршня, откуда х = .

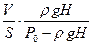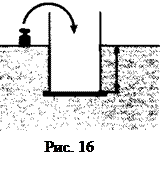
Задача 9. Цилиндрический сосуд с легким и тонким приставным дном, плотно прилегающим к стенкам сосуда, опущен в воду так, что дно находится на глу­бине Н=4 см, и удержи­вается неподвижно (ри­с.16). Гирю какой мини­мальной массы и куда на­до поставить на дно, чтобы оно отвалилось? Диаметр дна D=10 см, размеры ги­ри считать малыми по сравнению с диаметром со­суда.

Решение. Гирю нужно поставить как можно ближе к стенке сосуда — при этом необходимая для отрыва дна масса будет минимальной.

Будем считать приставное дно жестким. Тогда сила, с которой дно давит снизу на сосуд (а значит, и сила, действующая со стороны сосуда на дно), будет приложе­на в точке касания с противоположной от гири стороны. Запишем уравнение моментов относительно этой точки:

ρgH 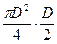= mgD, или m = 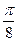ρHD ² =157 г. Это составит ровно половину массы вытесненной воды. Как только дно перестанет давить снизу на цилиндр и образуется небольшая щель — в нее войдет вода и дно отвалится.

Нужно сказать, что ответ сильно зависит от того, как «устроен» контакт дна с цилиндром — наша модель вза­имодействия, а потому и решение, не единственные.

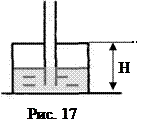Задача 10. В отверстие в дне перевернутого стакана, стоящего на горизонтальной плоскости, вставлена длинная тонкая трубка. Через трубку в стакан вли­вают воду. Высота стакана Н, площадь поперечного сечения S, масса М. Какой объем воды можно влить в стакан до момента, когда она начнет вытекать из-под стакана? Атмосферное давление р.

Краткое решение. Из условия равновесия получаем

Мg+рS = р₁S.

По закону Бойля - Мариотта имеем рН = р₁(Н - х).

Решая систему, получаем V = HS/(1 + SD/ Мg).

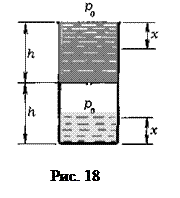Задача 11. Цилиндрический сосуд высоты 2h, поровну разде­ленный перегородкой, содер­жит в верхней части воду (ее плотность ρ), в нижней - воздух при атмосферном дав­лении p₀. В перегородке открывается небольшое от­верстие, так что вода начи­нает протекать в нижнюю часть сосуда. Какой толщины будет слой воды в нижней части сосуда, когда воздух начнет проходить из от­верстия вверх? Температура постоянна. Ускорение силы тяжести равно g.

Решение. Воздух из нижней части сосуда начнет проходить через отверстие вверх, когда давление его превысит гидростатическое давление воды на уровне отверстия, то есть при давлении p= p₀ + ρg(h–x), где х - понижение уровня воды в верхней части сосуда и, соответственно, толщина слоя воды в нижней части сосуда.

Так как температура воздуха не меняет­ся, согласно закону Бойля-Мариотта p₀hS=p(h–x)S, где S - площадь дна сосуда. Таким образом, р₀(h – x) + ρg(h – x)² = p₀h, откуда ρgx² – (2ρgh + p₀)x + ρgh² = 0. Решая это уравнение, находим х: 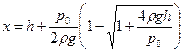(решение 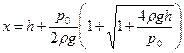не подходит, так как заведомо х<h.)

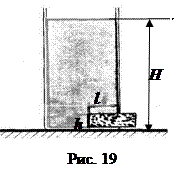Задача 12. В прямоугольный очень высокий сосуд налита жидкость плотности ρ. В одной из стенок у дна сосуда имеется прямоугольное отверстие высоты h, куда вдвинута на рас­стояние l невесомая пробка того же сечения (рис.19). Между пробкой и дном сосуда жид­кость не проникает. Коэффициент трения пробки о дно сосуда равен μ. Трение пробки о края сосуда пренебрежимо мало. При каком уровне жидкости над пробкой жидкость не сможет вытолкнуть пробку?

Решение. Обозначим высоту уровня жидкости над пробкой через Н. Запишем условие отсутствия движения пробки: р_срS ≥F_тр+рS, где р_ср= р + ρg(H+ h/2), S = а h (а - ширина пробки), F_тр = k(ρgH + р) lа.

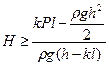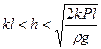Отсюда получаем при или .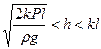

 

Задача 13. Цилиндрический бак наполнен доверху жидкостью плотности ρ. Сверху бак плот­но закрыт крышкой радиуса R. Снизу в баке имеется от­верстие площади s, закрытое пробкой массы m. Чтобы вытащить пробку из бака, нужно приложить силу f. С какой максимальной угловой скоростью можно вращать бак вокруг верти­кальной оси так, чтобы проб­ка не вылетала?

Решение. 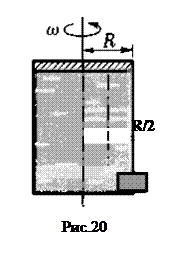Давление в жидкости во вращающемся баке на одной и той же глубине будет разным в центре сосуда и у стенок — давление нарастает по мере удаления от центра. Найдем, на сколько отличается давление у стенок от давления в центре.

Выделим мысленно тонкий горизонтальный столбик жидкости с площадью поперечного сечения σ (рис.20). Центр масс этого столбика движется по окружности ра­диуса R/2. Запишем уравнение движения столбика: 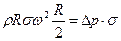(ρRσ — масса столбика, Δp·σ — результирующая сил давления, действующих на столбик справа и слева). Таким образом, давление в жидкости у стенки больше давления в центре на величину .

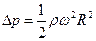Поэтому сила, действующая на пробку со стороны жид­кости, равна 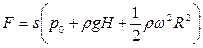, где p₀ - атмосферное давление, Н - высота бака. Запишем уравнение движения пробки: .

Как следует из условия, пробка вылетает из бака при F_тp = f + sρgH. Учитывая это, найдем угловую скорость вращения, при которой пробка вылетит: ω= .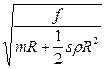

Задача 14. В цилиндрическом сосуде с площадью дна 125 см² находится вода. Когда в сосуд положили кубик льда, уровень воды повысился на 9 мм. Чему равна длина ребра ледяного кубика?

Решение. Представим себе, что кубик льда, помещенный в сосуд, растаял в воде. Масса воды в сосуде будет равна массе первоначальной воды (в сосуде без льда) плюс масса воды, образовавшейся из льда, то есть плюс масса кубика. Объем, занимаемый этой "дополнительной" водой, равен Vв = Sh; масса этой воды m = rвV= rвSh – равна массе ледяного кубика; но масса кубика равна m = rлVл= rл×а3 (а – длина ребра кубика). Следовательно, rвSh = rл×а3, откуда 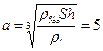см.

Задача 15. В цилиндрическом стакане с водой плавает льдинка, притянутая ко дну ниткой (рис). Когда льдинка растаяла, уровень воды в стакане понизился на Δh. Каково было натяжение нити? Площадь дна стакана S.

Решение. На основании второго закона Ньютона, запишем равенства:

Т = F_a – mg; F_a = p_вgV_п; m = ρ_лV_л. T- p_вgV_п - ρ_лV_лg (1)

V₁=V_в +V_п; V₂ =V_в+V'; V'=m_л/ρ_в; h₁ = h_в+V_п/S; h₂ =h_в + m_л/ρ_вS;

Δh=V_л/S - m_л /ρ_вS; V_п= (р_вSΔh+ ρ_лV_л)/ρ_в . Получаем Т= ρ_вgSΔh.

Задача 16. В сосуд с поперечным сечением 12 см², частично заполненный водой, положили деревянный кубик, ребро которого имеет длину 2 см. На сколько изменится уровень воды в сосуде? Плотность дерева принять равной 700 кг/м³. При помещении кубика вода не переливается через края сосуда.

Решение. Кубик, плавая в воде, вытеснит объем V = ΔhS. Объем вытесненной волы равен объему погруженной в воду части кубика. На кубик действует сила тяжести и архимедова сила: mg-ρ_вgV=0. Отсюда V = mg/ρ_вg = .

Изменение высоты уровня воды в сосуде составит Δh =V/S = 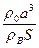≈ 4,7 мм.

Задача 17. Плотность некоторой жидкости меняется с глубиной по закону:

ρ(h)= ρ(0)(1+αh), где ρ(0) - известная постоянная. Для измерения константы α в жидкость опускают тяжелый цилиндр длиной l и сечением s, который висит вертикально на нити, привязанной к динамометру. Разность показаний динамометра равна ΔF в положениях, когда верхняя грань цилиндра совпадает с поверхностью жидкости и когда она же находится на глубине h = l от поверхности. Найти по этим данным величину α.

Решение. Разность показаний динамометра определяется разностью давлений на верхнюю и нижнюю грани цилиндра, находящегося в жидкости. Так как плотность жидкости меняется с глубиной по линейному закону, давление меняется по закону: p(h)=p(0)+p(0)g (h +αh2/2). Если m - масса цилиндра, то в первом случае показание динамометра равно F1= mg - ρ (0)g(l +αl2/2)s, а во втором – F2= mg - ρ (0)g(l +2αl2/2)s. По условию ΔF = F1 – F2, откуда находим: α = .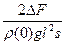

Задача 18. Какова минимальная масса проволоки из алюминия, которую следует намотать на пробку массы m=20 г, чтобы пробка вместе с проволокой полностью погрузилась в воду? Плотность пробки ρ_n= 0,5·10³ кг/м³, алюминиевой проволоки ρ_np= 2,7·10³ кг/м³, воды ρ=10³ кг/м³.

Решение. При полном погружении пробки с проволокой в воду выталкивающая сила будет равна r_вg(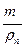 + 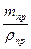), где m_np - масса проволоки. Эта сила будет уравновешивать cилу тяжести, действующую на пробку c проволокой, откуда r_вg( 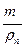+ 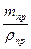)=(m+m_np)g, поэтому масса проволоки должна удовлетворять соотношению m_np= m 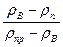= 31,7 г.

Задача 19. В колбе находится некоторое количество воды, в которой плавает пробка. На сколько процентов изменится объём надводной части пробки, если из колбы выкачать воздух? Плотностью образовавшихся после откачки паров воды пренебречь. Плотность воздуха 1,3 кг/м³.

Решение. Обозначим V₀- объем пробки, V₁и V₂ - объем надводной части пробки до и после откачки. Условия плавания пробки до и после откачки: ρ_вV₁g+ρ(V₀-V₁)g -ρ_пV₀g = 0;

ρ(V₀ -V₁)g - ρ_пV₀g = 0. Отсюда .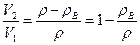

Подводная часть пробки потеряла в объеме .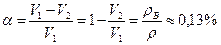

Задача 20. Сосуд заполнен жидкостью плотности ρ до уровня Н. Отверстие площади S в дне перекрыто снизу пластинкой, которая связана нитью с поплавком, наполовину погруженным в жидкость. С какой силой пластинка давит на дно, если при повышении уровня жидкости на величину h (при которой поплавок полностью погружен) жидкость начинает выдавливаться из отверстия? Массами поплавка, нити и пластинки пренебречь.

Краткое решение. Уравнения равновесия ρgНS+ F= F_А/2, ρg(Н+h)S=F_А.

F = .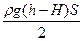

При h < Н вода вытекала бы также и в начальном положении.

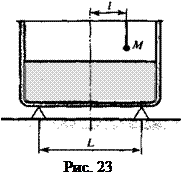Задача 21. Прямоугольный сосуд с водой стоит на двух опорах, разнесенных на расстояние L друг от друга. Над сосудом на перекладине подвешен на нити кусок свинца массой М на расстоянии l от цент­ра сосуда (рис.23). Силы реакции опор при этом равны N₁ и N₂. Нить удлиняют так, что свинец погружается в воду. Ка­кими станут после этого силы реакции опор? Плот­ность свинца в n раз боль­ше плотности воды.

Решение. Когда грузик окажется в воде, сила натяжения нити станет меньше на величину выталкивающей силы — силы Архимеда F_A=Mg/n.

Уровень воды в сосуде при этом поднимется, и сила давления воды на дно увеличится на такую же величину (третий закон Ньютона). Для симметричного сосуда точка приложения этой добавочной силы находится в середине дна сосуда.

Очевидно, что сумма сил реакций опор останется прежней: N'₁+ N'₂=N₁+N₂.

Поэтому, если сила N'₁, действующая со стороны левой опоры, станет на величину f больше прежней, то сила N'₂ станет на такую же величину меньше.

Из равенства нулю суммарного момента добавочных сил, действующих на систему: 2f L/2 =F_A l получаем f = F_A l /L = Mg l /(nL).

Тогда окончательно N'₁=N₁+ f = N₁+Mgl/(nL), N'₂= N₂- f = N₂- Mg l /(nL).

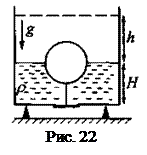
Задача 22. Цилиндрический сосуд, закрытый невесомым порш­нем площадью сечения S, со­держит газ под атмосферным давлением р₀. Объем газа при этом равен V₀. Сосуд погру­жают в воду (плотностью ρ_o) так, как показано на рисунке. Найти зависимость расстоя­ния х между поршнем и по­верхностью воды от модуля F силы, удерживающей нить, которая привязана к поршню.

Решение. 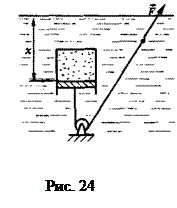Запишем уравнение состояния газа в цилиндре (закон Бойля — Мариотта), когда поршень находится на некоторой глубине х под водой: p0V0 = pV = phS, (1) где р — давление в цилиндре, а h - расстояние от днища цилиндра до поршня.

Условие равновесия поршня на глу­бине X –

pS + F = (p₀ + ρ₀gx)S. (2)

Условие равновесия цилиндра pS = (p₀+ ρ₀g(x-h))S + Mg, (3) где М - масса цилиндра. Решая совместно уравнения (1), (2), (3), получим: x = 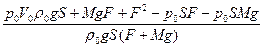или, если цилиндр невесом, x = 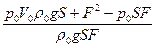. (5) Соотношения (4) и (5) справедливы, очевидно, лишь тогда, когда цилиндр полностью погружен в воду.

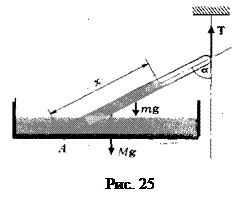
Задача 23. Тонкостенная трубка ртутного ба­рометра открытым концом опирается на дно чашки с ртутью. Закрытый конец удерживается вертикальной нитью, так что трубка составляет угол α с вертикалью (рис.25). Длина трубки l, масса m, плот­ность ртути ρ, атмосферное давление h мм рт. ст. Найти силу натяжения ни­ти. Размером погруженной в ртуть части трубки пренебречь. Площадь сечения труб­ки S.

Решение. Так как трубка барометра находится в равновесии, то сумма моментов всех сил, действующих На трубку со ртутью, относи­тельно любой оси должна быть равна нулю. Запишем условие равновесия для оси, пер­пендикулярной плоскости чертежа и про­ходящей через точку A, в которой трубка опи­рается на дно сосуда:

Тlsin α - mg 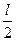sin α - Mg 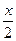sin α = 0. (1)

Здесь Т — сила натяжения нити, mg — сила тяжести трубки, Mg = ρxSg — вес ртути, находящейся в трубке, х — длина столбика ртути.

Давление столбика ртути в трубке равно атмосферному давлению, поэтому x = 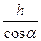. (2) Следовательно, из (1) и (2) T = 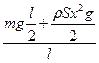= 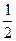g(m + ).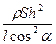

Задача 24. Цилиндрический стакан высоты Н, опущенный вверх дном в жид­кость плотности ρ, плавает погруженным до глубины h₁. Стакан, плаваю­щий дном вниз, погружен до глубины h₂. Найти атмосферное давление.

Решение. Пусть разница уровней жидкости наружи внутри перевернутого стакана равна х. Тогда по закону Паскаля ρgх + Р_о = Р, для запертого пе­ревернутого стакана по Бойлю - Мариотту Р₀Н = Р(Н - h₁+ х), из усло­вия равновесия перевернутого стакана (Р - Р_о) = mg/S, а для не перевернутого плавающего - ρgh₂ = mg/S. х = h₂. Получаем Р_о= ρgh₂(H + h₂ - h₁)/(h₁- h₂).

Задача 25. На квадратном де­ревянном плоту размером 2x2x0,3 м, сделанном из дерева плотностью 800 кг/м³, стоит человек массой 80 кг. На какое рас­стояние от центра плота он должен отойти, чтобы, край плота окунулся в воду?

Решение. Пусть в начальный момент человек находится в центре плота. Запишем условие равновесия системы «чело­век — плот» в виде Mg + mg = ρ_вgSh, где m — масса человека, M=ρV—масса плота, ρ_в — плотность воды, S — площадь плота, h — глубина погружения его в воду. Отсюда находим h = 0,26 м.

Теперь рассмотрим ситуацию, когда человек отошел от центра на расстояние l, и край плота окунулся в воду (см. рисунок). Поскольку система по-прежнему находится в равновесии, объем погруженной части плота измениться не должен:

Sh = SH - 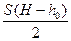, откуда находим h₀ = 0,22 м.

Нам осталось записать уравнение моментов сил относительно центра масс плота. Моменты создают следующие силы (только они и изображены на рисунке): сила тяжести человека mg, архимедова сила Р_А1, действующая на погруженную не заштрихованную на рисунке часть плота, и архимедова сила Р_А2, действующая на заштрихованный участок, причем точка ее приложения лежит в точке пересечения медиан выделенного тре­угольника (т. е. плечо этой силы равно L/2—L/3 = L/6, где L = 2 м — длина плота). Поэтому получаем равенство

mgl соs α + ρ_вL²h₀ 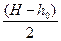sin α = ρ_вL² 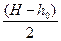g 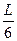, из которого, учитывая малость угла α, находим искомую величину l: l ≈ 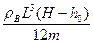≈ 0,67 м.

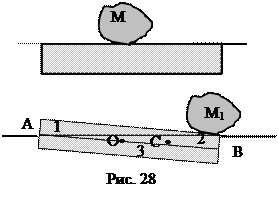Задача 26. Плавающая на поверхности пруда прямоугольная льдина, продольные размеры которой много больше её толщины, выдерживает груз массой 100 кг, помещённый в центр льдины. Какой груз можно разместить на краю льдины, чтобы он не касался воды?

Решение. Льдину считаем настолько длинной, что длина ее и диагональ практически равны между собой.

По условию равновесия груза на льдине в случае расположения его в центре льдины

ρ_лgV + Mg = ρ_вgV, где V – объем льдины; получаем V= M/(ρ_в- ρ_л) = 1м³.

При перемещении груза на край льды равновесие системы определяется равенством моментов сил, действующих на систему. При этом помним, что центр тяжести, а, значит, и точка приложения выталкивающей силы, действующей на треугольную фигуру, находится на расстоянии 1/3 от ее основания. Представив разрез льдины в виде трех фигур – равных по площади треугольников 1 и 2, и прямоугольника 3, определим точки приложения выталкивающей силы, действующей на части 2 и 3, находящиеся в воде. Для части 3 такой точкой является геометрический центр О. Точка С части 2 находится на расстоянии 2/3 l от точки А. Тогда объем подводной части V'=V₃+V₂=V-V₁ можно найти различными способами, например, правилом моментов относительно точки В: ΣМ_В= 0 ρ_лgV l /2 - ρ_вgV₃ l /2 - ρ_вgV₂ · l /3= 0; получим V'=0,075 м³.

Тогда правило моментов относительно противоположной точки льдины дает возможность рассчитать массу груза в точке В: ΣМ_А= 0 M₁g l /2 = ρ_в gV' l (2/3-1/2); M₁=1/3·0,075·10³ = 25 кг.

 

12	Поделиться:

Воспользуйтесь поиском по сайту: