 |
Применение ДП для решения задачи замены оборудования.
|
|
|
|
Постановка задачи. На некотором производстве рассматривается процесс эксплуатации оборудования в период времени длительностью n лет. Этот период условно разбивается на этапы (например, один этап – один год). В начале каждого этапа относительно оборудования принимается решение: продолжать эксплуатировать старое или заменить его новым оборудованием. Решение зависит от следующих четырех характеристик оборудования: производительности, величины эксплуатационных расходов, остаточной стоимости старого и стоимости нового оборудования. Отметим, что первые три характеристики старого оборудования определяются его возрастом. Эти характеристики определяют прибыль, получаемую от эксплуатации оборудования.
Алгоритм решения. Введем обозначения. Пусть t – возраст оборудования, t=0, 1, …, n, где n – длина планового периода; r(t) – стоимость продукции, производимой за год на единице оборудования, возраст которого t лет (производительность); u(t) – ежегодные затраты на обслуживание этого оборудования (эксплуатационные расходы); s(t) – остаточная стоимость оборудования; p – стоимость нового оборудования.
Первый этап метода динамического программирования – погружение задачи в семейство аналогичных задач. Рассмотрим при всех сформулированных условиях плановый период, включающий последние n-k лет. Будем считать, что возраст оборудования на начало k+1 –го года равен t лет. ясно, что  Если k=0, то получим исходную задачу.
Если k=0, то получим исходную задачу.
Введем функцию Беллмана – максимальное значение прибыли за последние n-k лет планового периода от использования оборудования, возраст которого на начало k+1 –го года равен t лет. Обозначим ее через  . Заметим, что это функция 2-х аргументов k и t. В принятых обозначениях возраст t=0 соответствует эксплуатации нового оборудования.
. Заметим, что это функция 2-х аргументов k и t. В принятых обозначениях возраст t=0 соответствует эксплуатации нового оборудования.
|
|
|
Перейдем ко второму этапу ДП – составлению уравнения Беллмана. Для этого рассмотрим 2 возможные ситуации на начало k+1 года.
Если на k+1-м году оборудование, возраст которого t лет, сохранить, то прибыль предприятия от его использования равна 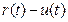 - стоимость произведенной продукции минус стоимость эксплуатационных издержек. Следуя принципу оптимальности, считаем, что все последующие годы решение о замене оборудования принималось оптимально. Поэтому общая прибыль за последние n-k лет в этом случае равна
- стоимость произведенной продукции минус стоимость эксплуатационных издержек. Следуя принципу оптимальности, считаем, что все последующие годы решение о замене оборудования принималось оптимально. Поэтому общая прибыль за последние n-k лет в этом случае равна
 (1.1)
(1.1)
Пусть на k+1 –ом году оборудование, возраст которого t лет, заменяется новым. Тогда прибыль предприятия за этот год состоит из выручки от продажи старого плюс стоимость произведенной продукции на новом оборудовании минус стоимость эксплуатационных издержек нового оборудования и минус затраты на его покупку, т.е. равна  . Согласно принципу оптимальности за последние n-k лет прибыль в этом случае равна
. Согласно принципу оптимальности за последние n-k лет прибыль в этом случае равна  . (1.2)
. (1.2)
Таким образом, если величина прибыли (1.1) больше или равна величине прибыли (1.2), то нужно работать на старом оборудовании, а противном случае оборудование следует заменить. Объединяя (1.1) и (1.2), запишем уравнение Беллмана:  , (1.3)
, (1.3)
Где первое выражение определяет прибыль, которая может быть получена за последние n-k лет на старом оборудовании, второе – при его замене. При этом предполагается, что переход к работе на новом оборудовании происходит за один этап.
Полагая в (1.3) k=n-1, получаем начальное условие для этого рекуррентного относительно аргумента k уравнения. Оно имеет вид уравнения одноэтапного процесса, для которого слагаемые  и
и  не имеют экономического смысла, и поэтому исключается, таким образом, прибыль от использования оборудования, возраст которого t лет, в последний год планового периода равна
не имеют экономического смысла, и поэтому исключается, таким образом, прибыль от использования оборудования, возраст которого t лет, в последний год планового периода равна
 (1.4)
(1.4)
|
|
|
Третий этап метода ДП – поиск решения уравнения (1.3) с начальными условиями (1.4) и построения по нему решения исходной задачи.
В уравнении (1.3) положим k=n-2:
 (1.5)
(1.5)
Далее полагаем в уравнении (1.3) k=n-3, n-4,…,0. после процесса оптимизации получим последовательность 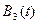 ,
,  , …,
, …, 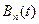 .
.
Исходные данные заносим в таблицу 1:
Таблица 1 – Исходные данные
| T | 0 | 1 | 2 | … | N |
| r(t) | r(0) | r(1) | r(2) | … | r(n) |
| u(t) | u(0) | U(1) | u(2) | … | u(n) |
| s(t) | s(0) | s(1) | s(2) | … | s(n) |
Далее составляем таблицу 2, заполняя ее значениями функции  . Каждое значение функции Беллмана соответствует либо политике сохранения оборудования, либо политике его замены. В каждой строке таблицы будем отделять такие значения жирной линией границы клетки.
. Каждое значение функции Беллмана соответствует либо политике сохранения оборудования, либо политике его замены. В каждой строке таблицы будем отделять такие значения жирной линией границы клетки.
Таблица 2
| T | 0 | 1 | 2 | … | n |
| B1(t) – прибыль за последний год | B1(0) | B1(1) | B1(2) | … | B1(n) |
| B2(t) – прибыль за последние 2 года | B2(0) | B2(1) | B2(2) | … | B2(n) |
| … | … | … | … | … | … |
| Bn(t) – прибыль за весь плановый период | Bn(0) | Bn(1) | Bn(2) | … | Bn(n) |
|
|
|


