Кольца Ньютона. Условия максимума и минимума. Радиусы светлых и темных колец Ньютона.

Ко́льца Нью́тона — кольцеобразные интерференционные максимумы и минимумы, появляющиеся вокруг точки касания слегка изогнутой выпуклой линзы и плоскопараллельной пластины при прохождении света сквозь линзу и пластину.

Интерференционная картина в виде концентрических колец (колец Ньютона) возникает между поверхностями одна из которых плоская, а другая имеет большой радиус кривизны (например, стеклянная пластинка и плосковыпуклая линза). Исаак Ньютон исследовав их в монохроматическом и белом свете обнаружил, что радиус колец возрастает с увеличением длины волны (от фиолетового к красному).

Удовлетворительно объяснить, почему возникают кольца, Ньютон не смог. Удалось это Юнгу. Проследим за ходом его рассуждений. В их основе лежит предположение о том, что свет — это волны. Рассмотрим случай, когда монохроматическая волна падает почти перпендикулярно на плосковыпуклую линзу.

Волна 1 появляется в результате отражения от выпуклой поверхности линзы на границе стекло — воздух, а волна 2 — в результате отражения от пластины на границе воздух — стекло. Эти волны когерентны, то есть у них одинаковые длины волн, а разность их фаз постоянна. Разность фаз возникает из-за того, что волна 2 проходит больший путь, чем волна 1. Если вторая волна отстает от первой на целое число длин волн, то, складываясь, волны усиливают друг друга.

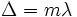— max, где - любое целое число, - длина волны.

Напротив, если вторая волна отстает от первой на нечетное число полуволн, то колебания, вызванные ими, будут происходить в противоположных фазах и волны гасят друг друга.

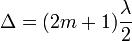— min, где - 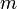любое целое число, 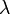- длина волны.

Для учета того, что в разных веществах скорость света различна, при определении положений минимумов и максимумов используют не разность хода, а оптическую разность хода. Разность оптических длин пути называется оптической разностью хода.

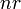— оптическая длина пути,

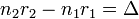— оптическая разность хода.

Если известен радиус кривизны R поверхности линзы, то можно вычислить, на каких расстояниях от точки соприкосновения линзы со стеклянной пластиной разности хода таковы, что волны определенной длины λ гасят друг друга. Эти расстояния и являются радиусами темных колец Ньютона. Необходимо также учитывать тот факт, что при отражении световой волны от оптически более плотной среды фаза волны меняется на , этим объясняется тёмное пятно в точке соприкосновения линзы и плоскопараллельной пластины. Линии постоянной толщины воздушной прослойки под сферической линзой представляют собой концентрические окружности при нормальном падении света, при наклонном — эллипсы.

Радиус k -го светлого кольца Ньютона (в предположении постоянного радиуса кривизны линзы) в отражённом свете выражается следующей формулой:

где

R — радиус кривизны линзы;

k = 2, 4, …;

λ — длина волны света в вакууме;

n — показатель преломления среды между линзой и пластинкой.

65. Волновой фронт электромагнитной волны. Принцип Гюйгенса - Френеля.

Волново́й фронт — это поверхность, до которой дошли колебания к данному моменту времени. Волновой фронт является частным случаем волновой поверхности.

Принцип Гюйгенса — Френеля — основной постулат волновой теории, описывающий и объясняющий механизм распространения волн, в частности, световых.

Принцип Гюйгенса — Френеля является развитием принципа, который ввёл Христиан Гюйгенс в 1678 году: каждая точка поверхности, достигнутая световой волной, является вторичным источником световых волн. Огибающая вторичных волн становится фронтом волны в следующий момент времени. Принцип Гюйгенса объясняет распространение волн, согласующееся с законами геометрической оптики, но не может объяснить явлений дифракции. Огюстен Жан Френель в 1815 году дополнил принцип Гюйгенса, введя представления о когерентности и интерференции элементарных волн, что позволило рассматривать на основе принципа Гюйгенса — Френеля и дифракционные явления.

Принцип Гюйгенса — Френеля формулируется следующим образом:

Фронтом волны точечного источника в однородном изотропном пространстве является сфера. Амплитуда возмущения во всех точках сферического фронта волны, распростр аняющейся от точечного источника, одинакова.