Построение графика на миллиметровой бумаге.

Построение графиков

При выполнении экспериментов в лабораторных работах часто приходится строить графики функциональных зависимостей вида Y=f(X).

При этом следует руководствоваться следующими правилами:

1. По оси абсцисс (горизонтальная ось) откладываются зна­чения независимой переменной (X), а по оси ординат - значения фун­кции (Y).

2. Размеры графика, толщина точек и соединяющих линий должны обеспечить необходимую точность отсчета, а также удобство пользования графиком.

3. Все точки, по которым строится график, должны быть отмечены на графике. При этом не следует специально откладывать соответствующие точкам значения на осях.

4. Нанесенные точки соединяются плав­ной кривой линией, то есть при построении линии следует применять сглаживание, учитывающее общий характер получаемой зависимости. При этом некоторые точ­ки, нанесенные на график, могут не вписываться в получаемую кривую (из-за неточностей измерений в этих точках). Благодаря тому, что измерение проводится в нескольких точках, применение сглаживания позволяет снизить влияние этих неточностей. На рис.1 приведены примеры построения графиков по одним и тем же точкам, правильного (рис.1, а) и – неправильного (рис.1, б). Толщина точек на примере выбрана большой для наглядности представления.

Рис.1. Примеры правильного (а) и неправильного (б) построения линий графиков

 

5. На координатных осях должны быть нанесены значения вели­чин X и Y, указаны единицы измерения в удобных величинах. Для выражения измеряемой величины с помощью числового значения целесообразно использовать десятичные кратные и дольные едини­цы, образованные от основной единицы и выраженные числовыми значениями между 0,1 и 1000. Этот подход обеспечивает наиболее удобное восприятие числовых данных.

Например: вместо 50000 Гц удобнее использовать 50 кГц, вместо 2·10^-3 А - 2мА.

 

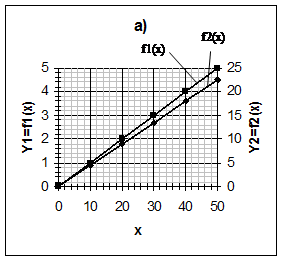
6. Если на одном графике строятся две зависимости Y₁=f₁(x) и Y₂ = f₂(x) и интервалы значений, в которых находятся величины Y1 и Y2, отличаются друг от друга более, чем в 1,5 раза, для каждой из этих функций на оси ординат следует откла­дывать свой масштаб (иначе погрешности графика для каждой из зависимостей будет сильно отличаться между собой). На рис.2, а показан пример правильного построения графика, на рис.2, б – неправильного (толщина точек на примере выбрана большой для наглядности).

Рис.2. Примеры правильного (а) и неправильного (б) выбора масштабов графика

 

5. График должен быть снабжен подписью, в которой содержатся сведения о том, какая зависимость построена и для какого прибора.

Расчет масштаба графика

 

От размеров графика зависит точность отсчета, однако при этом может пострадать удоб­ство пользования им. Поэтому масштаб графика рассчитывается ис­ходя из реальных условий.

При построении графиков градуировки приборов, погрешность, вносимую графиком (δ_гр), выбирают меньше погрешности самого при­бора (δ_пр) примерно в 5 раз. При этом суммарная погрешность δ_Σ(с уче­том погрешности, вносимой графиком) будет несущественно отличаться от погрешности самого прибора:

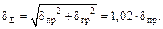
Построение графика на миллиметровой бумаге.

В случае построения графика на миллиметровой бумаге, абсолютная погрешность гра­фика в единицах длины выбирается равной Δl=0,5 миллиметра (половина цены деления миллиметровой сетки). Тогда с учетом приня­тых условий масштаб графика можно рассчитать по формуле

где А_н - номинальное значение (верхний предел) прибора; δ_пр – погреш­ность (класс точности) прибора, %; Δl - погрешность графика, мм.

Если график строится в интервале значений (не от нуля), то масш­таб графика рассчитывается по формуле

После расчета графика (масштаба) следует округлить полученный результат до ближайшей удобной для использования цифры. Масштаб должен выражать­ся числами 1, 2 или 5, умноженными на 10ⁿ, где п - целое число. Длина оси графика при этом определяется следующим образом:

Отсюда видно, что размеры графика определяются по­грешностью прибора и интервалом значений.

 

12Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: