 |
Абсолютная и условная сходимость.
|
|
|
|
Числовые ряды. Основные понятия.
Пример 1. Используя определение, исследовать ряд на сходимость 
.
Решение:
Составим частичные суммы ряда:
.
Таким образом, получим последовательность частичных сумм: 
.
Т.е. 
.
Найдем предел: 
. По определению ряд сходится и его сумма равна 0,5.
Пример 2. Показать, что ряд сходится и найти его сумму 
.
Решение:
Разложим общий член ряда в сумму простейших дробей
.
Запишем n-ую частичную сумму
Мы заметили, что (k-2)-й и k-й члены содержат одно и то же выражение с противоположными знаками.
Найдем предел
.
То есть данный ряд сходится и его сумма равна 0,3.
Пример 3. Исследовать ряд на сходимость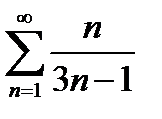 
.
Решение:
Пользуясь необходимым признаком сходимости, докажем расходимость ряда.
Найдем 
. Ряд расходится.
Задачи для самостоятельного решения
Исследовать ряды на сходимость:
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
Ответы:
1) s=13/2; 2) расходится; 3) s=7/2; 4) s=2; 5) расходится; 6) s=5/6; 7) s=1; 8) расходится; 9) s=22.
Достаточные признаки сходимости знакоположительных рядов.
Пример 1. Исследовать ряд на сходимость 
.
Решение:
Используем признак сравнения. Сравним члены данного ряда с членами гармонического ряда 
, который расходится: 
. Так как ряд с меньшими членами расходится, то и данный ряд с большими членами 
так же расходится.
Пример 2. Исследовать ряд на сходимость 
.
Решение:
Используем предельный признак сравнения. Возьмем обобщенный гармонический ряд 
. Он сходится, т.к. степень знаменателя больше 1. Вычислим предел отношения общих членов этих рядов
.
Получили конечный, не равный нулю, предел. Значит, ряды ведут себя одинаково. Исходный ряд также сходится.
|
|
|
Пример 3. Исследовать ряд на сходимость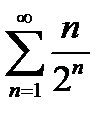 
.
Решение:
Используем признак Даламбера.
Вычислим предел отношения последующего члена к предыдущему:
. Ряд сходится.
Пример 4. Исследовать ряд на сходимость 
.
Решение:
Используем радикальный признак Коши.
Вычислим предел корня n-ой степени из общего члена:
. Ряд сходится.
Пример 5. Исследовать ряд на сходимость 
.
Решение:
Заметим, что
.
Будем исследовать на сходимость ряд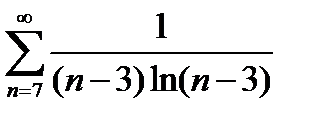 
Используем интегральный признак Коши.
Так как функция 
удовлетворяет условиям признака, а именно монотонна, положительна и 
при 
, то исследование сходимости ряда сводится к исследованию сходимости интеграла 
.
Интеграл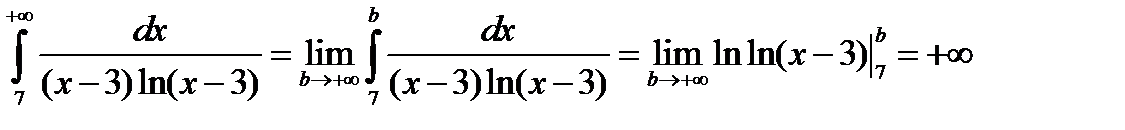 
расходится. Следовательно, расходится и ряд 
.
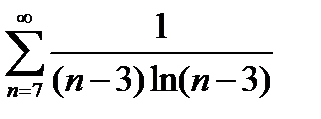По признаку сравнения, раз расходится ряд с меньшими членами, то расходится и ряд с большими членами. Значит, исходный ряд расходится.
Задачи для самостоятельного решения
Исследовать ряды на сходимость:
5. 
6. 
-
-
-
-
-
-
-
-
-
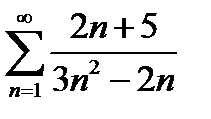
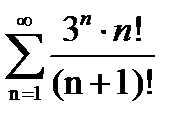
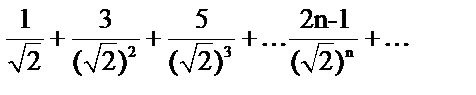
- а)
;
б)
. -
-
-
-
-
-
-
-
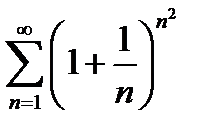
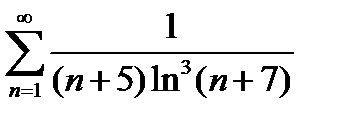
25. 
26. 
27. 
28. 
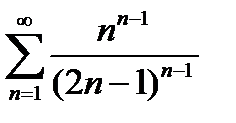
29. 
30. 
31. 
32. 
33. 
34. 
35. 
36. 
37. 
38. 
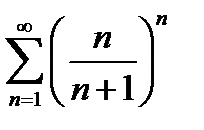
39. 
40. 
41. 
42. 
43. 
44. 
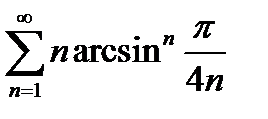
45. 
46. 
47. 
48. 
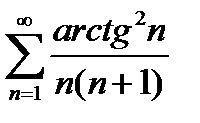
Ответы:
1) сходится; 2) сходится; 3) сходится; 4) расходится; 5) сходится; 6) расходится; 7) расходится; 8) сходится; 9) сходится; 10) расходится; 11) расходится; 12) сходится; 13) расходится; 14) сходится; 15) сходится; 16) а) сходится, б) сходится; 17) сходится; 18) сходится; 19) расходится; 20) расходится; 21) сходится; 22) расходится; 23) сходится; 24) расходится; 25) сходится; 26) расходится; 27) сходится; 28) сходится; 29) расходится; 30) сходится; 31) расходится; 32) расходится; 33) расходится; 34) расходится; 35) сходится; 36) сходится; 37) сходится; 38) расходится; 39) расходится; 40) сходится; 41) расходится; 42) сходится; 43) сходится; 44) сходится; 45) расходится; 46) сходится; 47) сходится; 48) сходится.
Абсолютная и условная сходимость.
Пример 1. Исследовать ряд на сходимость 
.
Решение:
|
|
|
Данный ряд знакопеременный, поэтому исследуем его на абсолютную сходимость. Применим обобщенный признак Даламбера:
.
Следовательно, ряд сходится абсолютно.
Пример 2. Исследовать ряд на сходимость 
.
Решение:
Применим признак Лейбница. Проверим выполнение условий признака:
а) 
, то есть члены ряда по модулю монотонно убывают. Первое условие признака выполнено;
б) 
.
Второе условие не выполнено и ряд расходится.
Пример 3. Исследовать ряд на сходимость 
.
Решение:
Данный ряд знакопеременный, поэтому исследуем его на абсолютную сходимость. Составим ряд из модулей членов исходного ряда: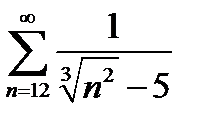 
.
Применим признак сравнения. Сравним члены данного ряда с членами обобщенного гармонического ряда 
, который расходится: 
. Так как ряд с меньшими членами расходится, то и ряд с большими членами 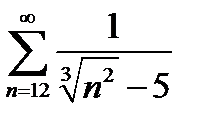так же расходится.
Итак, ряд, составленный из модулей членов исходного ряда расходится, поэтому продолжим исследование исходного ряда на условную сходимость. Для этого применим признак Лейбница.
Проверим выполнение условий признака:
а) 
, то есть члены ряда по модулю монотонно убывают. Первое условие признака выполнено;
б) 
. Второе условие выполнено.
Таким образом, исходный ряд сходится условно.
|
|
|
12 |
