 |
Задачи для самостоятельного решения
|
|
|
|
Исследовать на сходимость с помощью признака Лейбница:
1. 
2. 
3. 
4. 
Исследовать на абсолютную и условную сходимость:
5. 
6. 
7. 
8. 
9. 
10. 
11. 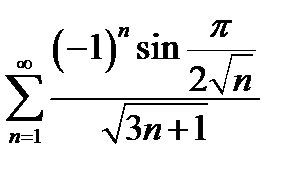
12. 
13. 
14. 
Ответы:
1) сходится; 2) сходится; 3) расходится; 4) сходится; 5) сходится абсолютно; 6) сходится абсолютно; 7) сходится абсолютно; 8) сходится абсолютно; 9) сходится условно; 10) сходится условно; 11) сходится условно; 12) сходится условно; 13) расходится; 14) сходится абсолютно.
Функциональные ряды.
Пример 1. Найти область сходимости функционального ряда 
Решение:
Применим обобщенный радикальный признак Коши:
 .
.
Что бы ряд сходился, получившийся предел должен быть меньше 1. Решив неравенство
 получаем
получаем 
Исследуем ряд при 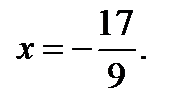 Получим знакочередующийся ряд
Получим знакочередующийся ряд 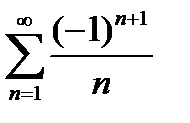 . Этот ряд по признаку Лейбница сходится условно.
. Этот ряд по признаку Лейбница сходится условно.
Таким образом, заданный ряд сходится при 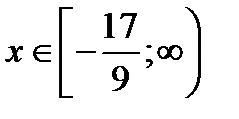 .
.
Пример 2. Найти радиус сходимости степенного ряда 
Решение:
Найдем радиус сходимости по формуле 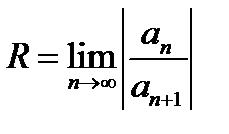 .
.

Получаем, что ряд сходится в круге  . Исследуем ряд на границе круга, то есть при
. Исследуем ряд на границе круга, то есть при  .
.
Если  имеем
имеем 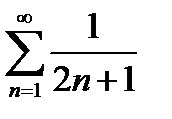 . Этот ряд расходится.
. Этот ряд расходится.
Если  имеем
имеем  Этот ряд сходится условно.
Этот ряд сходится условно.
Таким образом ряд сходится при  .
.
Пример 3. Вычислить  с точностью до 0,001.
с точностью до 0,001.
Решение:
Предварительно представим подынтегральную функцию в виде степенного ряда. Заменив в разложении функции 
 на
на 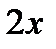 , получим:
, получим:
 .
.
Тогда

Полученный знакочередующийся ряд удовлетворяет условиям теоремы Лейбница. Четвертый член ряда по абсолютному значению меньше 0,001. Чтобы обеспечить требуемую точность, достаточно найти сумму первых трех членов. Следовательно,  .
.
Пример 4. Найти частное решение дифференциального уравнения  соответствующее начальным условиям
соответствующее начальным условиям  , в виде степенного ряда, найдя первые четыре ненулевые члена разложения. Составить таблицу полученного решения с шагом
, в виде степенного ряда, найдя первые четыре ненулевые члена разложения. Составить таблицу полученного решения с шагом  на отрезке
на отрезке  и построить его график. Вычисления вести с точностью до
и построить его график. Вычисления вести с точностью до  .
.
|
|
|
Решение:
Частное решение данного уравнения будем искать в виде степенного ряда

Из начального условия:  . Найдем значения
. Найдем значения  .
.
 .
.
Найдем вторую производную:

 .
.
Найдем третью производную:

Подставляем найденные значения в степенной ряд:
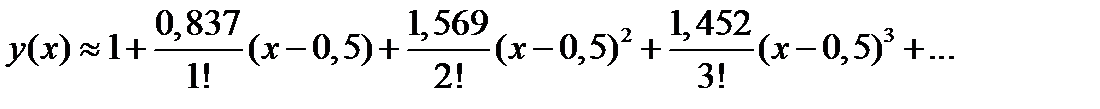 .
.
Получили приближенное частное решение данного дифференциального уравнения, удовлетворяющее заданному начальному условию:
 .
.
Составим таблицу значений полученного решения:

| 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | |
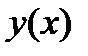
| 1,092 | 1,201 | 1,328 | 1,476 | 1,645 |
Построим график по найденным точкам:
Задачи для самостоятельного решения
Найти область сходимости данных рядов:
1. 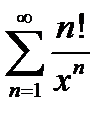
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 
13. 
14. Разложить функцию  в ряд Тейлора в окрестности точки
в ряд Тейлора в окрестности точки 
15. Найти первые пять членов ряда Тейлора для функции  в окрестности точки
в окрестности точки 
Разложить функции в ряд Маклорена:
16.  ;
;
17.  ;
;
18. 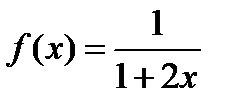 ;
;
19.  .
.
Разложить функции в ряд Тейлора:
20.  по степеням
по степеням 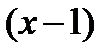 ;
;
21.  по степеням
по степеням 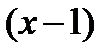 ;
;
22.  по степеням
по степеням  .
.
Вычислить приближенно:
23.  с точностью до
с точностью до 
24.  с точностью до
с точностью до 
25. 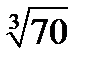 с точностью до
с точностью до 
26.  с точностью до
с точностью до 
27.  , взять 3 члена разложения, указать погрешность
, взять 3 члена разложения, указать погрешность
28.  , взять 2 члена разложения, указать погрешность
, взять 2 члена разложения, указать погрешность
Ответы:
1) расходится; 2) сходится абсолютно при  ; 3) сходится абсолютно при
; 3) сходится абсолютно при  ; 4) сходится при
; 4) сходится при 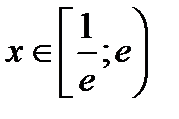 ; 5)
; 5)  ; 6)
; 6)  ; 7)
; 7)  ; 8)
; 8) 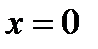 ; 9)
; 9)  ; 10)
; 10)  ;
;
11)  ; 12)
; 12)  ; 13)
; 13)  ; 14)
; 14)  ;
;
15)  ; 16)
; 16)  ; 17)
; 17)  ;
;
18)  ; 19)
; 19)  ; 20)
; 20)  ;
;
21)  ; 22)
; 22)  ; 23) 0,7788; 24) 0,17365; 25) 4,121; 26) 0,699; 27) 0,323, погрешность 0,0001; 28) 0,012, погрешность 0,001.
; 23) 0,7788; 24) 0,17365; 25) 4,121; 26) 0,699; 27) 0,323, погрешность 0,0001; 28) 0,012, погрешность 0,001.
Ряды Фурье.
Пример 1. Разложить функцию  в ряд Фурье и построить график суммы.
в ряд Фурье и построить график суммы.

Решение:
Данная функция терпит разрыв 1 рода в точке 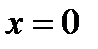 . Функция удовлетворяет условиям теоремы Дирихле. В данной задаче период
. Функция удовлетворяет условиям теоремы Дирихле. В данной задаче период  , а
, а  .
.
Разложим функцию в ряд Фурье:

Вычислим коэффициенты ряда. Поскольку функция разрывна в начале координат, то каждый коэффициент Фурье очевидным образом следует записать в виде суммы двух интегралов:
|
|
|
1) Первый интеграл:
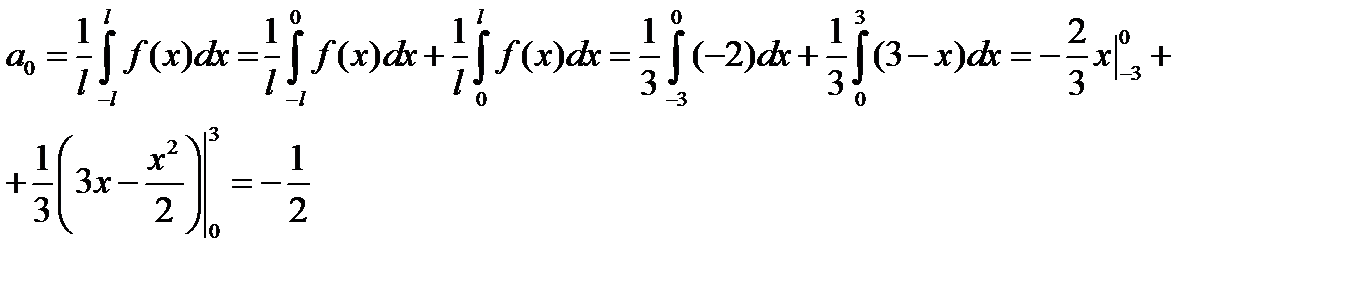
2) Второй интеграл:

3) Третий интеграл:

Подставим найденные коэффициенты Фурье в формулу:
 .
.
Полученный ряд Фурье сходится во всех точках отрезка  и его сумма
и его сумма  равна:
равна:
1) самой функции  в точках непрерывности функции,
в точках непрерывности функции,
2)  в точке разрыва
в точке разрыва  ,
,
3)  на концах отрезка
на концах отрезка
Построим график суммы ряда  . На интервале
. На интервале  строим прямую
строим прямую  , а на интервале
, а на интервале  — прямую
— прямую  . В точке разрыва
. В точке разрыва  —
—  , при
, при  —
— 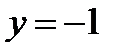 . И «продолжаем» график на всю числовую ось с периодом
. И «продолжаем» график на всю числовую ось с периодом  :
:

Пример 2.
Разложить функцию  в ряд Фурье.
в ряд Фурье.
Решение:
Наша функция удовлетворяет условиям теоремы Дирихле. В данной задаче период  , а
, а  . Заметим, что функция является нечетной. Поэтому будем раскладывать ее в ряд по синусам:
. Заметим, что функция является нечетной. Поэтому будем раскладывать ее в ряд по синусам:
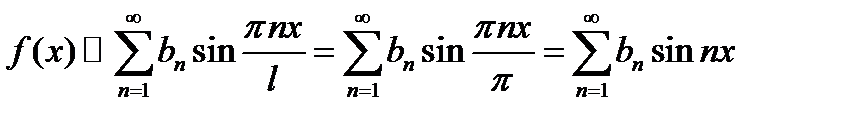 ,
,
где 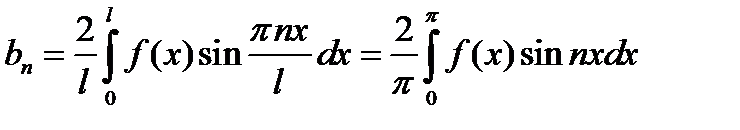 .
.
Вычислим коэффициенты

Подставим найденные коэффициенты Фурье в формулу:
 .
.
В точке  —
—  , на концах отрезка —
, на концах отрезка —  .
.
|
|
|
12 |


