Разрешающая способность микроскопа

Несмотря на то, что увеличение оптического микроскопа может быть сделано достаточно большим, возможность различения мелких деталей предмета ограничивается дифракционными явлениями. При прохождении света через мельчайшие детали предмета изображение их вследствие дифракции может терять резкость, может возникнуть нарушение геометрического подобия изображения предмету и, наконец, возможно полное исчезновение изображения. Поэтому, например, в оптическом микроскопе невозможно видеть фильтрующиеся вирусы, отдельные белковые молекулы и т. п.

Свойства оптической системы давать раздельное изображение двух близко расположенных светящихся (или освещенных) точек называют разрешающей способностью системы и характеризуют пределом разрешения, т. е. наименьшим возможным расстоянием между этими точками. Чем меньше предел разрешения, тем выше разрешающая способность оптического прибора.

Применяя это понятие к условиям микроскопирования биологических объектов, можно считать, что предел разрешения обусловливает наименьшую величину тех структурных деталей, которые могут различаться в препарате.

Разрешающая способность микроскопа в целом определяется разрешающей способностью объектива, в который непосредственно входят лучи света, дифрагировавшие на деталях предмета. Основным элементом, обусловливают им разрешающую способность объектива, является его апертурный угол.

Рассмотрим образование с помощью объектива изображения светящегося отверстия S достаточно малого диаметра d, на которое падает пучок параллельных монохроматических лучей (рис.3). Проходя через отверстие, свет испытывает дифракцию. Объектив собирает дифрагировавшие лучи н в сопряженной плоскости образует изображение S' отверстия. При этом возможны два случая. Во-первых, когда апертурный угол объектива q больше угла a дифракции лучей или равен ему (q≥a), тогда все дифрагировавшие лучи принимают участие в образовании изображения (рис. 3,а); в этом случае изображение будет геометрически подобно предмету. Во-вторых, когда апертурный угол q объектива, ограничивающий конус входящих в него лучей, меньше угла a дифракции лучей (q<a), тогда не все исходящие из отверстия лучи принимают участие в образовании изображения (рис. 3,б) в этом случае можно ожидать, что изображение не будет полностью подобно предмету. Степень нарушения подобия будет зависеть от того, какая часть дифрагировавших лучей не попадает в объектив и не принимает участия в образовании изображения.

Рис 3

Угол a дифракции лучей тем больше, чем больше длина волны λ и чем меньше диаметр d отверстия, т.е. a~λ/d. Тогда в предельном случае, когда q=a, между апертурным углом q, длиной волны λ и диаметром отверстия d можно установить аналогичное соотношение q~λ/d, откуда d~λ/q. Таким образом, диаметр d отверстия, при котором сохраняется подобие изображения предмету, может быть тем меньше, чем короче длина волны к и чем больше апертурный угол q объектива.

Перенося рассуждения на условия микроскопирования, можно считать, что диаметр d отверстия соответствует наименьшему размеру структурных деталей препарата, т.е. приравнять его пределу разрешения z объектива микроскопа z=d. Тогда можно сказать, что предел разрешения объектива z будет тем меньше, чем короче длина волны λ света, падающего на предмет, и чем больше апертурный угол q объектива.

В теории Аббе в качестве микроскопируемого предмета рассматривается дифракционная решетка (рис.4), которая освещается пучком перпендикулярно падающих на нее параллельных монохроматических лучей. Лучи, претерпевшие дифракцию на щелях решетки, собираются объективом Л в его фокальной плоскости, образуя систему дифракционных максимумов (0,1 и 1’, 2 и 2', 3 и 3' и т.д.). За фокальной плоскостью лучи, образующие максимумы различных порядков, расходятся и, пересекаясь между собой в сопряженной плоскости, дают на экране изображение решетки. Если в его образовании принимают участие лучи от всех максимумов (рис. 4,а), то изображение будет резким и геометрически подобным предмету.

Если с помощью диафрагмы Д уменьшать апертурный угол объектива (рис. 4,б), то лучи, образующие максимумы более высоких порядков, не попадут в линзу и не будут участвовать в образовании изображения. Изображение будет терять резкость и тем больше, чем меньшим будет апертурный угол. Если апертурный угол уменьшить так, что в линзу попадут только прямые лучи, образующие нулевой максимум (рис. 4,в), то экран будет равномерно освещен и изображения решетки не получится.

Как показал Аббе, для разрешения щелей в изображении дифракционной решетки необходимо, чтобы в образовании ее изображения участвовали лучи от максимумов нулевого и первого порядка хотя бы с одной стороны. Для этого направления лучей, образующих эти максимумы, должны быть в пределах апертурного угла объектива. Другими словами, апертурный угол объектива q должен быть больше угла φ₁ отклонения лучей, образующих максимум первого порядка, или в пределе равен ему: q≥φ₁. Предел разрешения в этом случае может быть приравнен периоду решетки: z=d. Тогда, используя формулу дифракционной решетки d=λ/sin φ₁ и подставляя в нее указанные величины, получим

Рис.4

т.е. предел разрешения численно равен отношению длины волны света к синусу апертурного угла объектива.

В более сильных микроскопах предмет освещается сходящимся пучком лучей, который образуется с помощью конденсора К. В этом случае вследствие концентрации света на небольшом участке предмета значительно повышается яркость изображения, а в связи с наличием лучей, падающих наклонно на предмет, улучшаются условия разрешения.

Пусть, например, пучок параллельных лучей падает на решетку под углом φ, равным апертурному углу θ, в таком случае (рис. 4) угол α₁ отклонения лучей, образующих максимум первого порядка, может быть приравнен удвоенному апертурному углу: α₁=2θ. В наших приближенных рассуждениях (рис. 4) это соответствует условию z=λ/2θ, а в теории Аббе формула для предела разрешения принимает вид

Дальнейшим усовершенствованием микроскопа явилось применение иммерсионного объектива. Так называют объектив, у которого пространство между наблюдаемым предметом и входной линзой заполняется жидкостью с показателем преломления, близким к стеклу, например глицерин (n=1,45) или монобромнафталин (n=1,65). При иммерсионном объективе, во-первых, значительно увеличивается яркость изображения и, во-вторых, повышается разрешающая способность микроскопа.

 

а) б)

Рис.5 Рис.6

Ход световых лучей показан сравнительно в простом («сухом») и иммерсионном объективах на рис. 6, на котором обозначено: П -препарат, С -покровное стекло, И -иммерсионная среда, О -фронтальная линза объектива и К -конденсор. При наличии между покровным стеклом и объективом воздуха (рис. 6,а) лучи, падающие на препарат под углом, большим предельного а, испытывают на границе стекла и воздуха полное внутреннее отражение и не попадают в объектив; отражение лучей происходит также и от передней поверхности объектива, на которую лучи падают под относительно большим углом.

При иммерсии свет от предмета до объектива проходит по оптически однородной среде и не дает потерь на отражение (рис 6,б). Это значительно повышает яркость изображения, что имеет существенное значение особенно для микроскопа с большим увеличением. (Для микроскопа с увеличением в 400 раз площадь изображения по сравнению с площадью предмета увеличивается в 160 000 раз, во столько же раз уменьшается его яркость по сравнению с яркостью предмета).

В иммерсионном объективе, где между предметом и объективом находится среда с показателем преломления n, длина волны λ_n света, проходящего в объектив, λ_n=λ/n, где λ -длина волны света в воздухе. Подставляя эти данные в формулу для предела разрешения, получим

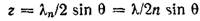
Величина А=sin θ для сухого или A_n=n sin θ для иммерсионного объектива называется численной апертурой и для сухого объектива обозначается на его оправе вместе о увеличением.

Максимальный апертурный угол может быть порядка 70°, тогда для сухого объектива численная апертура А=sin 70° = 0,94, для иммерсионного - при n - 1,5 А_п = 1,5-0,94 = 1,4.

При освещении предмета белым светом можно считать X = 0,555 мкм (длина волны, к которой глаз наиболее чувствителен), тогда предел разрешения для сухого микроскопа при прямом освещении z = λ/A = 0,5 нм, при наклонном освещении z = λ/A = 0,3 нм и для иммерсионного объектива z = λ /2Ап = 0,2 нм.

Для того чтобы эти объекты были различимы также и глазом, увеличение γ_м микроскопа должно быть не меньше величины, определяемой соотношением пределов разрешения глаза z_гл и микроскопа z_м: γ_м ≥ z_гл/z_м = 75/(0,2 - 0,3) = 250 - 400.

Такое увеличение называют полезным увеличением микроскопа. Практически (с некоторым запасом) увеличение микроскопа берут равным γ_м = (500- 1000)A, где А - численная апертура.

Дальнейшее повышение разрешающей способности оптического микроскопа достигается уменьшением длины волны света, с помощью которого производится исследование, например путем применения ультрафиолетового излучения. Для этого имеются специальные микроскопы с кварцевой оптикой, снабженные приспособлением для фотографирования наблюдаемых объектов.

Рис.7 внешний вид современного бинокулярного микроскопа

В настоящее время ограничения оптического микроскопа, обусловленные дифракцией света, потеряли свою остроту в связи с открытием электронного микроскопа, имеющего разрешающую способность на несколько порядков выше.

Конструкция микроскопа.

На рис 7 показан стереомикроскоп и пронумерованы его основные части:

1. Окуляры

2. Револьвер со сменными объективами

3. Объектив

4. Микровинт

5. Макровинт

6. Предметный столик

7. Источник света

8. Конденсор и диафрагма

9. Система крепления и перемещения препарата

123	Поделиться:

Воспользуйтесь поиском по сайту: