 |
Алгебраических преобразований.
|
|
|
|
А неопр.0^0, 1^¥, ¥^0 с помощью тождества
f(x)^g(x)=e^g(x)lnf(x) сводятся к неопр вида 0
#21,22 Многочлен Тейлора
Пусть ф-ция f(x) есть м-н Pn(x) степени n: f(x) = Pn(x)=a0+a1x+…+anxn=A0+A1(x-x0)+…+An(x-x0)n. Для нахож. коэфф. An продиф. Pn(x) n раз. Pn(n)(x) = n(n-1)(n-2)…2*1*An. При x = x0 получим Pn(x) = Pn(x0) + (P’n(x0)/1!)(x-x0) +… …+ (P(n)n(x0)/n!)(x-x0)n
Ф-ла Тейлора:
f(x) = f(x0) + (f’(x0)(x-x0)/1!) +…+(f(n)(x0) (x-x0)n/n!)+Rn(x)
Rn(x) – остат. член ф-лы показ. погреш. рав-ва f(x)» Pn(x)
Rn(x) в форме Лагранжа: f (n+1)(x0+q(x-x0))(x-x0)(n+1)/(n+1)!
Rn(x) в форме Пеано: o((x-x0)n) при x®x0
Ф-ла Маклорена
При x0=0 получаем частный случай Тейлора – ф-лу Маклорена f(x)=f(0)+f’(0)x/1!+f’’(0)x2/2!+.+f(n)(0)(xn)/n!+f(n+1)(c)(xn+1)/(n+1)!
f(x)»f(x0)+f’(x0)(x-x0)/1!+…+f(n)(x0)(x-x0)n/n!
1) e x=1+x/1!+x2/2!+x3/3!+…+xn/n!+ecxn+1/(n+1)! 2) sin x=x-x3/3!+x5/5!-…+(-1)n(x2n+1)/(2n+1)!+(-1)n+1(x2n+3)/(2n+3)!* cos c 3) cos x=1-x2/2+x4/4-…+(-1)nx2n/(2n)!+(-1)n+1x2n+2/(2n+2)!* cos c
4) ln (1+x)=x-x2/2+x3/3-x4/4+…+(-1)n-1xn/n+(-1)nxn+1/(n+1)(1+c)n+1
5) (1+x)k =1+kx+k(k-1)x2/2!+…+k(k-1)…(k-n+1)xn/n!+
+k(k-1)…(k-n)(1+c)k-n-1xn+1/(n+1)!
#23 Локальный экстремум ф-и 1-й переменной
Если произв. ф-ции y=f(x) в точке х0 не определена или равна нулю, то х0- точка экстремума ф-ции.
Локальный экстремум ф-ции 1-й перемен
д-во: (необх) Если дифф. Ф-ция y=f(x) имеет
экстремум в точке x0, то ее произв. в этой точке
равна нулю: f’(x0)=0.
(дост) Если непрерывная ф-ция y=f(x) дифф. В некоторой d-окр. критич. точки х0 и при переходе через нее(слева направо) произв. f’(x) меняет знак с плюса на минус, то х0 есть хmax, с минуса на плюс, то хmin
#24 Вычисляется вторая производная f''(x) и с ее
помощью находятся промежутки выпуклости
(f''(x)<0), вогнутости (f''(x)>0) и точка перегиба
(f''(x)=0). Точки перегиба:
Точка х0 наз. точкой перегиба графика ф-ции y=f(x), если $ e-окр. точки х0 такая, что в ее левой (х< х0) и правой (х> х0) половине график ф-ции у= f(x) имеет разные направления выпуклости.
Точки перегиба д-во:
(необх) Если ф-ция у= f(x) имеет в точке х0 вторую произв. и график этой ф-ции имеет перегиб в точке х0, то f''(х0)=0 (достат) Если f''(х) при переходе через точку х0, в которой она равна нулю или не сущ., меняет знак, то точка графика с абциссой х0 есть точка перегиба.
|
|
|
#25 Наклонные и горизонтальные асимптоты
Асимптота – прямая, расстояние до которой от точки, лежащей на кривой, стремится к нулю при неограниченном удалении от начала координат этой точки по кривой. Ур-е наклонной асимптоты будем искать в виде y = kx+ b. Пусть М(х;у) – произвольная точка кривой. По ф-ле расст. от точки до прямой находим: d = |(kx-y+b)/Ö k2 +1|. d®0 Û limx®¥(kx-y+b) = 0 Û Û limx®¥(y/x) = limx®¥(k+b/x(®0)) Þ k = limx®¥(y/x) Þ Þ b= limx®¥(y-kx). Если k=0, то b – гориз. асимптота.
Вертикальные асимптоты
Прямая x=a явл. вертик. асимптотой y=f(x), если limx®a f(x)= ¥, или limx®a-0 f(x)= ¥ limx®a+0 f(x)= ¥.
#26 Частные производные ф-ии неск.
Переменных:: Частной производной функции
f(x,y) 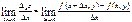
по х называется предел отношения
частного приращения ∆хz к приращению ∆х,
когда х→0 (если этот предел существует)(1)
Аналогично определяется частная производная
функции z=f(x,y) по у. Для частной производной
функции нескольких переменных, производную
функции одной переменной называют
переменной иногда обыкновенной.
#27 Дифференциал: диф. функции y=f(x) в данной т. x соответствующим приращением Dx называют главную относительную Dx часть приращения этой функции в т.x
Дифференциалом функции Z называется главная линейная часть приращения функции
Adx + Bdy = (Dz/Dx)dx + (Dz/Dy)dy Из условия дифф. Функции в Р0 следует сущ. касат.
плоскости к поверхности Z = f(x,y)
Геометрический смысл: приращение
кординаты касательной.
Dy=f’(x0)dx; f’(x0)=tga
#28 Локал. экстр. Функции нескольких перемен:
Р- min Z = f(P) если для любых P принад. окресн. Р0 следует:Z(p)>Z(Р0)
Р- max Z = f(P) если для любых P принад. окресн. Р0 следует:Z(p)<Z(Р0)
Необх. Условие экстремума. Часные производные первого порядка = 0
|
|
|
Стационарные точки это точки в которых выполняются необходимые условия экстремума.
#29 Предел функции: говорят что существует lim(x®a)f(x)=A Û когда существует окр-ть (e;A) такая что "окр-ти(d;A) $ окр-ть(0) (d;A) "xÎокр-ть(0) (d;A)Þf(x)Îокр-ть(e;A)
Предел ф-ции в точке Пусть ф-ция y = f (x) определена в некоторой окрестности точки x0. Число А наз пределом ф-ции в точке x0, если для "e>0 найдется такое d>0, что для всех x¹x0, удовл. нер-ву
|x-x0|<d, вып. нер-во | f (x) - A|<e. lim x®x0 f (x) = A.
Предел ф-ции на бесконечности Пусть ф-ция y=f(x) определена в промежутке (-¥; ¥). Число А наз. пределом ф-ции f(x) при x®¥, если ("e>0 $М(e)>0, "x: |х|>М Þ |f(x) - А| < e) Û limx®¥ f(x)=А.
#30 Бесконечно большие функции
Ф-ция y=f(x) наз. ббф
1) при x®x0, если ("М>0 $d>0 "x:|x-x0|<d, x¹x0 Þ |f(x)|>M) Û Û limx®x0f(x) = ¥
2) при x®¥, если ("М>0 $N>0 "x:|x|>N Þ |f(x)|>M) Û Û limx®¥f(x) = ¥." ббф в окрестности точки x0 явл. неогранич.
Т. о связи функций и ее предела: чтобы тело и являлось бы (lim(x®a)f(x)=A)Û(f(x)-A=a(x)) была бы бесконечно малой функциеей при x®a
Бесконечно большие функции: функция y=f(x) называется бесконечно большой при x®a если lim(x®a)f(x)=¥
Сравнение роста Б.Б.: u(x) v(x) – Б.б. при x®a
lim(x®a)n(x)/v(x) (1*)
(1*)=¥ u(x)-более высокого порядка роста чем v(x)
(1*)=0 v(x)-Б.б. более высокого порядка роста
(1*)=const u(x) и v(x) – одного порядка роста
(1*)=1 u(x)»v(x) при x®a
если не сущ lim(x®a)a(x)/b(x) – не сравниваются
#31 Ф-ция нескольких переменных.
Пусть даны два мн-ва DÌR2 и FÌR1 и пусть указано правило, по которому каждой точке (x;y)ÎD соответствует некоторое число zÎF. Вэтом случае говорят, что задана ф-ция z = f(x,y) с областью определения D и областью значений в F. При этом х и у называют независ. перемен., а z – зависимой переменной. Ф-ция двух перем. допуск. геометр. истолкование. Каждой точке М0(х0,у0) области D в системе координат Oхуz соотв. точка М0(x0,y0,z0), где z0-аппликата точки М. Совокупность всех этих точек есть некоторая поверхность, которая и будет геометрически изображать данную ф-цию z = f(x,y).
|
|
|


