Главная | Обратная связь | Поможем написать вашу работу!

Случайные величины, их функциональные и числовые характеристики

Математика

Программа, методические указания и задания контрольной и самостоятельной работы для студентов заочной формы обучения направления:

«Торговое дело-100700», «Менеджмент-080200»

Сокращенная образовательная программа

Квалификация выпускника - бакалавр

Новосибирск 2011

Кафедра общегуманитарных дисциплин

Математика. Теория вероятностей и математическая статистика: Программа, методические указания и задания контрольной работы 2 для студентов заочной формы обучения «Торговое дело-100700», «Менеджмент-080200»

Составитель: Вахромеева Т.В., доцент, Новосибирск: НФ РГТЭУ - 2011, 31 стр.

Рецензент: Бертик И.А., доцент кафедры общегуманитарных дисциплин

Методические указания рекомендованы к изданию кафедрой общегуманитарных дисциплин, протокол от «17» ноября 2011г.

Содержание

1. Правила выбора варианта контрольной работы................ 4

2. Содержание дисциплины................................... 5

3. Вопросы для подготовки к экзамену...........................7

4. Варианты контрольной работы............................ 8

5. Методические указания для решения задач................... 26

Правила выбора варианта контрольной работы, ее оформление и зачета

1. В процессе изучения дисциплины «Математика» студент должен выполнить две контрольные работы, задачи которых содержатся в разделе «Варианты контрольной работы». Не следует приступать к выполнению контрольного задания до решения достаточного количества задач по учебному материалу, соответствующему этому заданию. Опыт показывает, что чаще всего неумение решить ту или иную задачу контрольного задания вызывается тем, что студент не выполнил это требование.

2. Контрольная работа должны быть оформлена в соответствии с настоящими правилами. Работа, выполненная без соблюдения этих правил, не засчитываются и возвращаются студенту для переработки.

3. Каждую контрольную работу следует выполнять в отдельной тетради, чернилами любого цвета, кроме красного, оставляя поля для замечаний рецензента.

4. На обложке тетради должны быть разборчиво написаны фамилия, имя, и отчество студента, факультет (институт), номер группы, название дисциплины (Теория вероятностей), номер контрольной работы, номер варианта. В конце работы следует поставить дату ее выполнения и расписаться.

5. Номер варианта контрольной работы, которую выполняет студент, должен совпадать с последней цифрой номера его зачетной книжки.

6. Решения задач надо располагать в порядке возрастания номеров. Условия задач следует переписать в тетрадь.

7. При решении задач нужно обосновать каждый этап решения исходя из теоретических положений курса.

Решение задач и примеров следует излагать подробно, объясняя все выполненные действия и используемые формулы. Решение каждой задачи должно доводиться до окончательного ответа, которого требует условие. В промежуточные вычисления не следует вводить приближенные значения корней, числа p, e и т. д.

Полученный ответ следует проверить способами, вытекающими из существа данной задачи. Так, например, вычислив неопределенный интеграл, нужно проверить, равна ли подынтегральная функция производной от полученной первообразной. Полезно также, если это возможно, решить задачу несколькими способами и сравнить полученные результаты.

8. Срок проверки контрольных работ – 10 рабочих дней. Студенты обязаны сдавать письменные контрольные работы не позднее, чем за 10 дней до начала экзаменационной сессии. В противном случае они не будут допущены к зачетам и экзаменам.

9. После получения прорецензированной работы студент должен исправить все отмеченные рецензентом ошибки и недочеты, внести в решения задач рекомендуемые рецензентом изменения или дополнения и прислать работу для повторной проверки. В связи с этим рекомендуем при выполнении контрольной работы оставить в конце тетради несколько чистых листов для внесения исправлений и дополнений впоследствии.

В случае незачета работы и отсутствия прямого указания рецензента на то, что студент может ограничиться представлением исправленных решений отдельных задач, вся работа должна быть выполнена заново.

При представленных на повторную проверку исправлениях обязательно должны находиться прорецензированная работа и рецензия на нее. Вносить исправления в сам текст работы после ее рецензирования запрещается.

10. Прорецензированные контрольные работы вместе со всеми исправлениями и дополнениями, сделанными по требованию рецензента, следует сохранять.

На экзамен студент должен явиться с рецензией на выполненную контрольную работу. Без предъявления преподавателю прорецензированных контрольных работ студент к экзамену не допускается.

Содержание дисциплины

Основные понятия и основные теоремы теории вероятностей. Схема Бернулли.

Предмет и задачи теории вероятностей. Статистические закономерности, примеры применения теории вероятностей в экономике.

Опыт, случайное событие. Относительная частота, ее устойчивость. Построение математической модели случайного опыта: пространство элементарных исходов. Алгебраические операции над событиями. Аксиоматическое построение теории вероятностей. Примеры вероятностных моделей. Классическая вероятностная схема. Элементы комбинаторики. Геометрическая вероятность.

Условная вероятность. Теоремы сложения и умножения вероятностей. Независимость событий. Формулы полной вероятности и Бейеса. Схема Бернулли.

Формируемые компетенции: ПК-1, ПК-3.

Случайные величины, их функциональные и числовые характеристики

Определение случайной величины. Дискретные и непрерывные случайные величины. Ряд распределения и функция распределения дискретной случайной величины. Плотность распределения и функция распределения непрерывной случайной величины. Основные числовые характеристики случайных величин (математическое ожидание, дисперсия, среднее квадратичное отклонение) и их свойства.

Распределения дискретных случайных величин: биномиальное, Пуассона. Распределения непрерывных случайных величин: равномерное, показательное, нормальное. Центральная предельная теорема (в упрощенной формулировке Ляпунова), локальная и интегральная теоремы Муавра-Лапласа.

Понятие случайного вектора (системы случайных величин) на примере двух случайных величин. Функция распределения случайного вектора. Независимые случайные величины. Числовые характеристики системы случайных величин: ковариация, коэффициент корреляции двух случайных величин.

Формируемые компетенции: ПК-1, ПК-3.

Математическая статистика

Предмет и основные задачи математической статистики. Выборка и способы ее представления. Эмпирическая функция распределения. Гистограмма и полигон относительных частот. Числовые характеристики выборочного распределения.

Точечные оценки параметров распределения по выборке. Оценки математического ожидания и дисперсии случайной величины и свойства этих оценок. Квантиль распределения. Интервальные оценки: доверительные интервалы и доверительная вероятность. Доверительные интервалы для параметров нормально распределенной генеральной совокупности.

Элементы теории корреляции. Проверка статистических гипотез

Формируемые компетенции: ПК-1, ПК-3, ПК-32.

Вопросы для подготовки к экзамену

1. Основные понятия теории вероятностей. Операции над событиями.

2. Аксиоматическое построение теории вероятностей. Классическая вероятностная схема.

3. Элементы комбинаторики и вычисление вероятности событий. Геометрическая вероятность.

4. Теорема сложения вероятностей.

5. Условная вероятность. Независимость событий. Теорема умножения вероятностей.

6. Формула полной вероятности.

7. Формула Бейеса.

8. Вероятность событий в схеме Бернулли.

9. Локальная и интегральная теоремы Муавра – Лапласа.

10. Определение случайной величины. Функция распределения и ее свойства.

11. Ряд распределения, полигон и функция распределения дискретной случайной величины.

12. Плотность распределения и функция распределения непрерывной случайной величины.

13. Математическое ожидание дискретной и непрерывной случайной величины.

14. Дисперсия и среднее квадратическое отклонение дискретной и непрерывной случайной величины.

15. Распределения дискретных случайных величин: биномиальное, Пуассона. Их числовые характеристики.

16. Равномерное и показательное распределения, их числовые характеристики.

17. Нормальное распределение и его числовые характеристики.

18. Понятие случайного вектора на примере системы двух случайных величин. Закон распределения системы двух дискретных случайных величин. Условные законы распределения. Независимые случайные величины.

19. Числовые характеристики системы случайных величин.

20. Предельные теоремы теории вероятностей.

21. Статистические оценки.

Варианты контрольной работы

Вариант 0

1. В коробке 30 одинаковых юбилейных монет. Известно, что 5 из них имеют нестандартный процент содержания золота. Случайным образом выбирают три монеты. Вычислите вероятность того, что: а) все монеты имеют нестандартный процент содержания золота; б) только одна монета имеет нестандартный процент содержания золота.

2. Магазин получил две равные по количеству партии одноименного товара. Известно что 25% первой партии и 40% второй партии составляет товар первого сорта. Какова вероятность того, что наугад выбранная единица товара будет не первого сорта?

3. Задан закон распределения дискретной случайной величины X:

X	- 2	- 1
p	0,02	0,38	0,30	p	0,08	0,04	0,02

Найдите:

а) неизвестную вероятность p;

б) математическое ожидание M, дисперсию D и среднее квадратическое отклонение s данной случайной величины;

в) функцию распределения F(x) и построить её график;

г) закон распределения случайной величины Y, если её значения заданы функциональной зависимостью .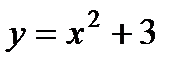

4. Известно, что вероятность опоздания ежедневного поезда на станцию равна 0,2. Какова вероятность того, что в течение 200 дней поезд опоздает на станцию а) 50 раз; б) от 100 до 150 раз?

5. Дана выборка количества сделок, совершенных фирмой по работе с недвижимостью за 20 дней.

1) Построить вариационный ряд.

2) Построить статистический ряд частот
3) Построить эмпирическую функцию распределения. и изобразить ее график
4) Найти выборочные характеристики: среднее, дисперсию, среднее квадратичное отклонение.
5) Найти 95% доверительный интервал для математического ожидания генеральной совокупности, если генеральная совокупность распределена по нормальному закону

6. Изучается зависимость количества продаж от расходов на рекламу

Расходы на рекламу х_i, млн. р.

0,5

1,5

2,5

3,5

4,5

Количества продаж y_i, тыс. ед.

34,4

34,8

36,1

37,7

37,3

37,5

39,6

40,9

43,6

1. Оценить тесноту линейной связи между признаками по данным выборки с помощью выборочного коэффициента линейной корреляции

2. Найти уравнение линейной регрессии , где ,

3. Изобразить на координатной плоскости точки с координатами () и прямую регрессии

Вариант 1

1. В студенческой группе 20 девушек. Известно, что 5 из них не любят читать детективы. Случайным образом выбирают трех девушек и дарят им по детективу. Вычислите вероятность того, что: а) все девушки оценят этот подарок; б) только одна девушка оценит этот подарок.

2. Товаровед плодоовощной базы определяет сорт поступившей от постоянного поставщика партии яблок. Известно. что в среднем 40% выращенного поставщиком урожая составляют яблоки первого сорта. Вероятность того, что товаровед признает первосортную партию первым сортом, равна 0,85. Кроме того, он может допустить ошибку, сочтя непервосортную партию первосортной, с вероятностью 0,2. Какова вероятность того, что он неверно установит сорт партии яблок?

3. Задан закон распределения дискретной случайной величины X:

X	- 2	- 1
p	0,06	p	0,12	0,24	0,33	0,14	0,03

Найдите:

а) неизвестную вероятность p;

б) математическое ожидание M, дисперсию D и среднее квадратическое отклонение s данной случайной величины;

в) функцию распределения F(x) и построить её график;

г) закон распределения случайной величины Y, если её значения заданы функциональной зависимостью y = x²+2.

4. Вероятность нормального расхода электроэнергии за день на предприятии бытового обслуживания равна 0,7. Какова вероятность того, что из 90 дней предприятие нормально расходует электроэнергию: а) в течение 60 дней; б) от 60 до 90 дней?

5. Дана выборка количества сделок, совершенных фирмой по работе с недвижимостью за 20 дней.

1) Построить вариационный ряд.

6. Изучается зависимость количества продаж от расходов на рекламу

Расходы на рекламу х_i, млн. р.

0,5

1,5

2,5

3,5

4,5

Количества продаж y_i, тыс. ед.

12,3

16,3

16,4

16,0

18,5

17,3

20,0

19,5

19,0

19,7

2. Найти уравнение линейной регрессии , где ,

3. Изобразить на координатной плоскости точки с координатами () и прямую регрессии

Вариант 2

1. В ящике 18 одинаковых бутылок минеральной воды без этикеток. Известно, что треть из них «Карачинская». Случайным образом выбирают 3 бутылки. Вычислите вероятность того, что среди них:

а) только минеральная вода сорта «Карачинская»;

б) ровно одна бутылка этого сорта.

2. В двух одинаковых коробках находятся карандаши «Конструктор». Известно, что треть карандашей в первой коробке и ¼ во второй имеют твердость ТМ. Наугад выбирается коробка, из нее наугад извлекается один карандаш. Он оказывается твердости ТМ. Какова вероятность того, что он извлечен из первой коробки?

3. Задан закон распределения дискретной случайной величины X:

X	- 2	- 1
p	0,16	0,25	0,25	0,16	0,10	p	0,03

Найдите:

а) неизвестную вероятность p;

б) математическое ожидание M, дисперсию D и среднее квадратическое отклонение s данной случайной величины;

в) функцию распределения F(x) и построить её график;

г) закон распределения случайной величины Y, если её значения заданы функциональной зависимостью

y = 4½x½ - 1.

4. Известно, что вероятность рождения мальчика равна 0,51, а девочки 0,49. Какова вероятность того, что 300 новорожденных окажется:

а) 150 мальчиков;

б) от 150 до 200 мальчиков?

5. Дана выборка количества сделок, совершенных фирмой по работе с недвижимостью за 20 дней

1) Построить вариационный ряд.

6. Изучается зависимость количества продаж от расходов на рекламу

Расходы на рекламу х_i, млн. р.

0,5

1,5

2,5

3,5

4,5

Количества продаж y_i, тыс. ед.

39,5

40,3

40,7

40,8

43,1

42,7

45,3

46,2

47,4

49,5

2. Найти уравнение линейной регрессии , где ,

3. Изобразить на координатной плоскости точки с координатами () и прямую регрессии

Вариант3

1. В нижней палате парламента 40 депутатов, среди которых первая партия имеет 20 представителей, вторая – 12 представителей, третья 5 представителей, а остальные считают себя независимыми. Случайным образом выбирают трех депутатов. Вычислите вероятность того, что среди них:

а) только представители первой партии,

б) только один депутат из первой партии.

2. Два специалиста ОТК проверяют качество выпускаемых изделий, причем каждое изделие с одинаковой вероятностью может быть проверено любым из них. Вероятность выявления дефекта первым специалистом равна 0,8, а вторым – 0,9. Из массы проверенных изделий наугад выбрано одно, оно оказалось с дефектом. Какова вероятность того, что ошибку допустил второй контролер?

3. Задан закон распределения дискретной случайной величины X:

X	- 2	- 1
p	0,05	0,12	0,18	0,30	p	0,12	0,05

Найдите:

а) неизвестную вероятность p;

б) математическое ожидание M, дисперсию D и среднее квадратическое отклонение s данной случайной величины;

в) функцию распределения F(x) и построить её график;

г) закон распределения случайной величины Y, если её значения заданы функциональной зависимостью y =5x - 2.

4. При оценке качества продукции было установлено, что в среднем третья часть выпускаемой фабрикой обуви имеет различные дефекты отделки. Какова вероятность того, что в партии из 200 пар, поступившей в магазин:

а) будут иметь дефекты отделки 60 пар;

б) не будут иметь дефектов отделки от 120 до 148 пар.

количества сделок, совершенных фирмой по работе с недвижимостью за 20 дней.

5. Дана выборка количества сделок, совершенных фирмой по работе с недвижимостью за 20 дней.

1) Построить вариационный ряд.

6. Изучается зависимость количества продаж от расходов на рекламу

Расходы на рекламу х_i, млн. р.

0,5

1,5

2,5

3,5

4,5

Количества продаж y_i, тыс. ед.

32,4

34,8

37,1

38,0

38,7

38,6

39,9

43,8

43,5

2. Найти уравнение линейной регрессии , где ,

3. Изобразить на координатной плоскости точки с координатами () и прямую регрессии

Вариант 4.

1. К экзамену приготовлено 24 одинаковых ручки. Известно, что треть из них имеет фиолетовый стержень, остальные – синий стержень. Случайным образом отбирают три ручки. Вычислить вероятность того, что:

а) все ручки имеют фиолетовый стержень;

б) только одна ручка имеет фиолетовый стержень.

2. Пассажир может приобрести билет в одной из двух касс. Вероятность обращения в первую кассу составляет 0,4, а во вторую – 0,6. Вероятность того, что к моменту приходя пасажира нужные ему билеты будут распроданы, равна 0,35 для первой кассы и 0,7 для второй. Пассажир посетил одну из касс и приобрел билет. Какова вероятность того, что он приобрел его во второй кассе?

3. Задан закон распределения дискретной случайной величины X:

X	- 2	- 1
p	p	0,29	0,12	0,15	0,21	0,16	0,04

Найдите:

а) неизвестную вероятность p;

б) математическое ожидание M, дисперсию D и среднее квадратическое отклонение s данной случайной величины;

в) функцию распределения F(x) и построить её график;

г) закон распределения случайной величины Y, если её значения заданы функциональной зависимостью y = ½x½.

4. По данным телеателье установлено, что в среднем 20% цветных телевизоров выходят из строя в течение гарантийного срока. Какова вероятность того, что из 225 проданных цветных телевизоров будут работать исправно в течение гарантийного срока: а) 164 телевизора; б) от 172 до 184 телевизоров.

5. Дана выборка количества сделок, совершенных фирмой по работе с недвижимостью за 20 дней.

1) Построить вариационный ряд.

6. Изучается зависимость количества продаж от расходов на рекламу

Расходы на рекламу х_i, млн. р.(одинаковое для всех вариантов)

0,5

1,5

2,5

3,5

4,5

Количества продаж y_i, тыс. ед.

21,0

23,0

23,7

23,8

25,8

27,6

28,4

29,7

31,7

31,6

2. Найти уравнение линейной регрессии , где ,

3. Изобразить на координатной плоскости точки с координатами () и прямую регрессии

Вариант 5

1. На витрине 32 одинаковых булочки. Известно, что среди них четверть булочек с изюмом, остальные с корицей. Случайным образом отбирают три булочки. Вычислите вероятность того, что:

а) все выбранные булочки с изюмом;

б) только одна булочка с изюмом.

2. Укупорка банок производится двумя автоматами с одинаковой производительностью. Доля банок с дефектом укупорки для первого автомата составляет 1%, а для второго 0,5%. Какова вероятность того, что наугад взятая банка будет иметь дефект укупорки?

3. Задан закон распределения дискретной случайной величины X:

X	- 2	- 1
p	0,08	0,10	0,14	0,17	0,19	0,18	p

Найдите:

а) неизвестную вероятность p;

б) математическое ожидание M, дисперсию D и среднее квадратическое отклонение s данной случайной величины;

в) функцию распределения F(x) и построить её график;

г) закон распределения случайной величины Y, если её значения заданы функциональной зависимостью

4. Установлено, что третья часть покупателей при посещении модного магазина приобретает себе одежду. Какова вероятность того, что из 150 посетителей магазина:

а) ровно 50 человек приобретут товар;

б) от 100 до 120 человек приобретут товар?

5. Дана выборка количества сделок, совершенных фирмой по работе с недвижимостью за 20 дней.

1) Построить вариационный ряд.

6. Изучается зависимость количества продаж от расходов на рекламу

Расходы на рекламу х_i, млн. р.

0,5

1,5

2,5

3,5

4,5

Количества продаж y_i, тыс. ед.

27,6

28,8

29,6

31,1

30,9

31,3

33,1

34,6

35,1

37,2

2. Найти уравнение линейной регрессии , где ,

3. Изобразить на координатной плоскости точки с координатами () и прямую регрессии

Вариант 6

1. В упаковке 12 одинаковых книг. Известно, что каждая третья книга имеет дефект обложки. Случайным образом выбирают 3 книги. Вычислите вероятность того, что среди них:

а) все книги имеют дефект обложки;

б) только одна книга имеет этот дефект.

2. Два контролёра производят оценку качества выпускаемых изделий. Вероятность того, что очередное изделие попадет к первому контролеру, равна 0,55; ко второму контролеру контролеру – 0,45. Первый контролёр выявляет дефект с вероятностью 0,8, а второй – с вероятностью 0,9. Вычислите вероятность того, что изделие с дефектом будет признано годным к эксплуатации.

3. Задан закон распределения дискретной случайной величины X:

X	- 2	- 1
p	0,42	0,23	p	0,10	0,06	0,03	0,01

Найдите:

а) неизвестную вероятность p;

б) математическое ожидание M, дисперсию D и среднее квадратическое отклонение s данной случайной величины;

в) функцию распределения F(x) и построить её график;

г) закон распределения случайной величины Y, если её значения заданы функциональной зависимостью y = -2x + 1.

4. Известно, что в данном технологическом процессе 10% изделий имеют дефект. Какова вероятность того, что в партии из 400 изделий:

а) не будут иметь дефекта 342 изделия;

б) будут иметь дефект от 30 до 52 изделий.

5. Дана выборка количества сделок, совершенных фирмой по работе с недвижимостью за 20 дней.

1) Построить вариационный ряд.

6. Изучается зависимость количества продаж от расходов на рекламу

Расходы на рекламу х_i, млн. р.

0,5

1,5

2,5

3,5

4,5

Количества продаж y_i, тыс. ед.

30,6

32,8

32,1

33,7

35,1

39,2

37,4

39,7

42,3

43,4

2. Найти уравнение линейной регрессии , где ,

3. Изобразить на координатной плоскости точки с координатами () и прямую регрессии

Вариант7

1. В туристической группе 15 человек, среди которых только 5 человек хорошо говорят по - английски. В Лондоне группу случайным образом расселили в два отеля (3 человека и 12 человек соответственно). Вычислить вероятность того, что из членов группы в первом отеле: а) все туристы хорошо говорят по - английски; б) только один турист хорошо говорит по - английски.

2. Покупатель может приобрести нужный ему товар в двух магазинах. Вероятности обращения в каждый из двух магазинов зависят от их местоположения и соответственно равны 0,3 и 0,7. Вероятность того, что к приходу покупателя нужный ему товар не будет распродан, равна 0,8 для первого магазина и 0,4 для второго. Какова вероятность того, что покупатель приобретет нужный ему товар?

3. Задан закон распределения дискретной случайной величины X:

X	- 2	- 1
p	0, 04	0, 08	0, 32	0, 31	0, 15	0, 08	p

Найдите:

а) неизвестную вероятность p;

б) математическое ожидание M, дисперсию D и среднее квадратическое отклонение s данной случайной величины;

в) функцию распределения F(x) и построить её график;

г) закон распределения случайной величины Y, если её значения заданы функциональной зависимостью y = x² – 1.

4. Установлено, что предприятие бытового обслуживания выполняет в срок в среднем 60% заказов. Какова вероятность того, что из 150 заказов, принятых в течение некоторого времени, будут выполнены в срок:

а) ровно 90 заказов;

б) от 93 до 107 заказов.

5. Дана выборка количества сделок, совершенных фирмой по работе с недвижимостью за 20 дней.

1) Построить вариационный ряд.

2) Построить статистический ряд частот
3) Построить эмпирическую функцию распределения. и изобра

12 Следующая ⇒

Воспользуйтесь поиском по сайту: