Методические рекомендации по выполнению контрольной работы

Для решения задачи 1 см. глава 1, § 1 – 5.

ЗАДАЧА 1.

На складе университета хранится 28 одинаковых упаковок писчей бумаги. Известно, что в четырех из них содержится бумага более низкого качества. Случайным образом выбирают три упаковки бумаги. Вычислить вероятность того, что среди них:

а) нет упаковок с бумагой более низкого качества,

б) есть одна упаковка такой бумаги.

Решение. Общее число возможных элементарных исходов для данных испытаний равно числу способов, которыми можно извлечь 3 упаковки бумаги из 28 упаковок, то есть – число сочетаний из 28 элементов по 3.

а) подсчитаем число исходов, благоприятствующих интересующему нас событию (нет упаковок с бумагой более низкого качества). Это число исходов ровно числу способов, которыми можно извлечь 3 упаковки бумаги из 24 упаковок (столько упаковок содержит бумагу высшего сорта),то есть

искомая вероятность равна отношению числа исходов, благоприятствующих событию, к числу всех элементарных исходов:

б) подсчитаем число исходов, благоприятствующих данному событию (среди трех упаковок бумаги ровно 1 упаковка содержит бумагу более низкого качества): две упаковки можно выбрать из 24 упаковок: способами, при этом одну упаковку нужно выбирать из четырех: способами. Следовательно, число благоприятствующих исходов равно

Искомая вероятность равна отношению числа исходов, благоприятствующих данному событию, к числу всех элементарных исходов .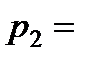

Ответ: а) 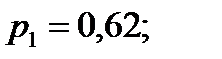б)

 

ЗАДАЧА 2.

Магазин получает электролампочки с двух заводов, причем доля первого завода составляет 25 %. Известно, что доля брака на этих заводах равна соответственно 5 % и 10 % от всей выпускаемой продукции. Продавец наугад берет одну лампочку. Какова вероятность того, что она окажется бракованной?

Решение: Обозначим через А событие – «лампочка окажется бракованной». Возможны следующие гипотезы о происхождении этой лампочки: «лампочка поступила с первого завода», «лампочка поступила со второго завода». Так как доля первого завода составляет 25 %, то вероятности этих гипотез равны соответственно:

Условная вероятность того, что бракованная лампочка выпущена первым заводом – вторым заводом – Искомую вероятность того, что продавец взял бракованную лампочку, находим по формуле полной вероятности: .

Ответ:

Для решения задачи 3 см. глава 6, § 1 – 3; глава 7, § 1 – 2; глава 8 § 1 – 3.

ЗАДАЧА 3.

Задан закон распределения дискретной случайной величены Х:

Х	– -4	– -2
р	00,05	р	00,12	00,23	00,32	00,14	00,04

Найдите:

а) неизвестную вероятность р,

б) математическое ожидание М, дисперсию D и среднее квадратическое отклонение данной случайной величены;

в) функцию распределения F(x ) и построить ее график;

г) закон распределения случайной величины Y, если ее значения заданы функциональной зависимостью

Решение:

а) так как сумма всех вероятностей должна равняться единице, то получим уравнение

Отсюда ;

б) математическое ожидание М это сумма всех произведений значений случайной величины на их вероятности:

Дисперсия D=

Среднее квадратическое отклонение = ;

в) если <

если – 4< <

если – 2< <

если 0< 0,05 + 0,1 + 0,12 = 0,15 + 0,12 = 0,27

если 2< 0,27 + 0,23 = 0,5;

если 4< 0,5 + 0,32 = 0,82;

если 6< 0,82 + 0,14=0,96;

если х >8, то F(x)=Р(Х < х)= 0,96 + 0,04=1.

Итак, функция распределения может быть записана так:

F (x) =

График этой функции приведен на рисунке:

 

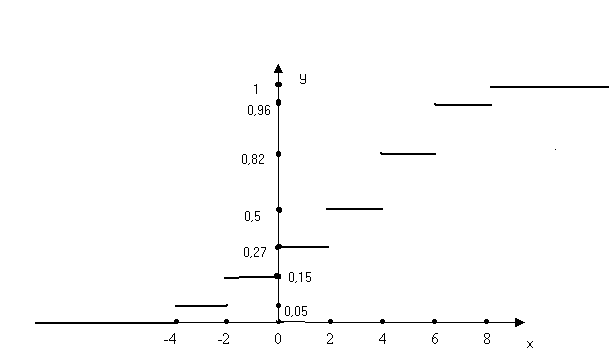
г) сначала найдем значения случайной величены Y.

По условиям задачи

Поэтому

Составим таблицу вида.

Y			– 1
P	0,05	0,1	0,12	0,23	0,32	0,14	0,04

Чтобы получить закон распределения случайной величены Y, необходимо:

1) рассмотреть ее значение в порядке возрастания;

2) сложить вероятности, соответствующие совпадающим значениям данной таблицы.

Итак, закон распределения случайной величены Y:

Y	– 1
Р	0,12	0,33	0,37	0,14	0,04

Для решения задачи 6 см. глава 5, §2, §3.

ЗАДАЧА 4.

Известно, что вероятность положительного исхода некоторого опыта равна 0,125. Найдите вероятность того, что в серии из 128 опытов положительный исход произойдет:

а) в 20 опытах;

б) от 12 до 20 опытов.

Решение:

а) воспользуемся локальной теоремой Лапласа. Вероятность того, что в n =128 испытаниях, в каждом из которых вероятность появления события равна равна к=20 раз (безразлично, в какой последовательности) приближенно равна

 

Так как

то

Значение функции находим в таблице (см. например, , стр. 461):

Итак,

Отметим, что таблица функции приведена только для положительных значений. Если же значение получилось отрицательным, то знак минус можно просто опустить в силу четности функции ;

б) воспользуемся интегральной теоремой Лапласа. Вероятность того, что в n =128 независимых испытаниях событие наступит от К₁=12 до К₂ =20 раз приближенно равна:

Так как ,

то

Значение функции также находим в специальной таблице (см. например приложение2). В таблице Для отрицательных значений х используют эту же таблицу, учитывая, что является нечетной функцией, то есть Итак, . Отсюда

Ответ:

 

 

Литература

1. Гмурман В. Е. Теория вероятностей и математическая статистика. — М. Высшая школа, 2009.

2. Гмурман В. Е. Руководство к решению задач по теории вероятностей и математической статистике. — М. Высшая школа, 2008.

3.Справочник по математике для экономистов: Учебное пособие / под ред.проф. В.И.Ермакова, М.: Инфра -М, 2009.- 464с.

4.Щипачев В.С. Высшая математика.Учебник для вузов.-5-е изд.,-М.: Высшая школа.2001.-479с.

5.Математика для экономистов: электронный учебник/ С.И.Макаров.- Москва.: Кнорус, 2009.

 

 

⇐ Предыдущая12

Поделиться:

Воспользуйтесь поиском по сайту: