Теоретический анализ модулятора на диоде

 

Поставленная задача анализа относится к классу нелинейных задач электродинамики, и её решение требует наличие достаточно мощных вычислительных средств. В то же время существует ряд приближённых методов анализа, позволяющих найти приемлемое решение, не прибегая к значительным затратам физического и машинного времени. Одним из них является квазилинейный метод, обычно применяемый для анализа нелинейных цепей при квазигармоническом характере протекающих в них токах и напряжениях [5], [7].

Суть метода заключается в том, что при определённых условиях ток или напряжение в нелинейной цепи может считаться периодическим процессом. В радиотехнических цепях основанием для такого допущения является наличие колебательных цепей в составе анализируемой цепи или системы. Периодический характер процесса, например тока в нелинейной цепи, позволяет представить его разложением в ряд Фурье:

i(t)=I₀+I₁cos(w ₀ t+ j ₀)+I₂cos(2 w ₀ t+2 j ₀)+…,                 (4.1)

где I_k – амплитуда k- ой гармоники тока;

I₀ – постоянная составляющая;

w₀ – частота первой гармоники;

j₀ – её начальная фаза.

Полагая, что ток вызывается некоторым воздействием, например, напряжением

U(t)=U₀cos(w ₀ t+ j ₀),                                        (4.2)

можно записать между амплитудами воздействия и отклика в виде:

                                         I_k(U₀)=Y_k(U₀)U₀,                                (4.3)

где Y_k(U₀) – проводимость нелинейной цепи по k – ой гармонике, зависящая от амплитуды воздействия.

Подобная зависимость может быть записаны и для постоянной составляющей, и для амплитуды какой-либо высшей гармоники. При этом зависимость проводимости от амплитуды воздействия, естественно, выражается другой функцией. Если фазовый сдвиг тока не совпадает с фазовым сдвигом входного напряжения (цепь является инерционной), то проводимость, связывающая комплексные амплитуды тока и напряжения, также является комплексной.

Таким образом, наличие нелинейного элемента («безынерционного» полупроводникового диода или варикапа) в составе модулятора – отражателя может быть учтено применением квазилинейного метода.

Основная задача расчёта – анализ тока в схемном эквиваленте вибратора, к которому последовательно подключён диод, а на диод подано модулирующее напряжение (рис 3.1). Это необходимо для определения параметров модуляции тока вибратора и создаваемого им поля в точке приёма.

В цепи действуют три источника напряжения – ЭДС высокочастотного колебания Е1, навязанного внешним полем, ЭДС модулирующего процесса U_МОД и постоянная ЭДС смещения Е_СМ. Значения параметров ЭДС модулирующего процесса U_МОД и смещения Е_СМ определяются внешними источниками соответствующих напряжений. Амплитуда Е₀ гармонической ЭДС Е1=Е₀cos(w₀t+ j₀) может быть рассчитана по формуле:

                                  (4.4)

где h_Д – действующая высота вибратора;

P_T,G_T – мощность передатчика и коэффициент направленного действия его антенны;

W=120 p - волновое сопротивление свободного пространства;

R – расстояние от передатчика до вибратора;

 - отношение потоков мощности поступающего на экран сигнала и сигнала, прошедшего через экран – коэффициент экранировки.

Равенство (4.4) предполагает нахождение точки приёма в дальней зоне, хотя в реальном случае она может находиться и в ближней зоне. Очевидно, что для ближней зоны равенство (4.4) не справедливо. Для полуволнового вибратора действующая высота равна 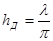, где l - длина волны.

Мощность передатчика, излучающего зондирующий сигнал, в (4.4) берётся в ваттах, тогда результат выражается в вольтах.

В качестве примера рассчитаем значение амплитуды наведённой ЭДС при облучении вибратора сигналом передатчика с расстояния R, при напряжение l=0,3м, мощности Р_Т=1Вт и Р_Т=4Вт, К_Э=G_T=1.

Рис.4.1. Зависимость амплитуды Е₀, ЭДС высокочастотного колебания Е1, навязанного внешним полем, от расстояния R.

При R=10м и Р_Т=1Вт Е₀ =0,074В. Приведённый пример показывает, что амплитуда наведённой ЭДС невелика, и при не больших значениях U_МОД возможна аппроксимация вольтамперной характеристики диода полиномом четвертого порядка:

i(t)» a₁U(t)+a₂U ²(t)+a₃U ³(t)+a₄U ⁴(t),                     (4.5)

где a₁, a₂, a₃, a₄ – коэффициенты аппроксимирующего полинома;

U(t) – напряжение на диоде.

Применяя квазилинейный метод, полагаем

U(t)=Е_СМ+U_МОД(t)+Е₀cos(w₀t)                           (4.6)

и находим значения для токов второй и третей гармоники:

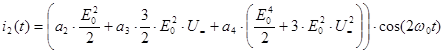,  (4.7)

,                                              (4.8)

где U_-=Е_СМ+U_МОД(t).

Дальнейшее выделение из (4.7) и (4.8) коэффициента модуляции М даёт следующий результат:

,  (4.9)

,    (4.10)

где

,    (4.11)

,                     (4.12)

   ,                               (4.13)

М₂ – коэффициент модуляции для тока второй гармоники;

М₃ – коэффициент модуляции для тока третей гармоники;

d₂ – относительный уровень нелинейности М₂;

U_M – амплитуда (половина размаха) модулирующего процесса.

Как видно из (4.11) и (4.13), коэффициенты модуляции зависят линейно от амплитуды модулирующего колебания. Кроме того, коэффициент модуляции тока второй гармоники имеет нелинейные искажения, отражённые в d₂. Эти искажения присутствуют принципиально в любом случае, у нас они появились только для второй гармоники из-за того, что мы ограничились четвёртой степенью полинома при аппроксимации зависимости тока от напряжения в нелинейном элементе. При увеличении порядка аппроксимирующего полинома нелинейные искажения появятся и в коэффициенте модуляции для тока третей гармоники. Правда, необходимо отметить, что в нашей задаче уровни сигналов незначительны, поэтому аппроксимация степенным рядом четвёртого порядка соответствует хорошей степени приближения.

Для обеспечения оптимальной работы системы необходимо решить задачу оптимизации, которая заключается в максимизации коэффициентов модуляции при заданном уровне нелинейных искажений (в нашем случае уровень нелинейных искажений пропорционален амплитуде модулирующего колебания) и при условии согласования вибратора на частоте зондирующего колебания (см. главу 1.1). Ясно, что при прочих равных условиях, увеличение одного коэффициента модуляции приведёт к уменьшению второго, поэтому нужно выбрать оптимальное соотношение между коэффициентами модуляции второй и третей гармоники.

Для примерной количественной оценки коэффициентов модуляции рассчитаем их на примере конкретного диода. В качестве диода возьмём арсенид галевый высокочастотный диод, вольтамперная характеристика которого записана в виде:

i=I₀(e^au-1),                                        (4.14)

где I₀ » 4,5 ×10^-8А, а=20В^-1.

Разлагая (4.14) в ряд Маклорена и ограничиваясь четвёртой степенью, можно получить:

,                 (4.15)

Сопоставляя выражения (4.15) и (4.5), и подставляя значения для а, получим a₁ =9×10^-7(А/В), a₂ =9×10^-6(А/В²), a₃ =6×10^-5(А/В³), a₄ =3×10^-4(А/В⁴).

Теперь необходимо подобрать смещение диода таким образом, чтобы дифференциальное сопротивление диода в рабочей точке было равно сопротивлению вибратора на частоте зондирующего сигнала. Из курса “Теория радиотехнических сигналов и цепей” известно, что дифференциальное сопротивление определяется значением производной функции напряжения от тока. В нашем случае известна обратная функция (зависимость тока от напряжения), поэтому мы можем найти дифференциальную проводимость. Возьмём производную от выражения (4.14) по напряжению, получим:

Y_ДИФ =a × I₀ ×× e^au,                                   (4.16)

Выразим из (4.16) u и вместо подставим Е_СМ, тогда получится следующее выражение для Е_СМ:

,                              (4.17а)

или

   ,                        (4.17б)

Подставляя значения для а и R_ДИФ=75Ом в (4.17б), получим Е_СМ» 0,48В.

Далее, задаваясь допустимым уровнем нелинейных искажений, найдём значение для амплитуды U_M из (4.12). Возьмём коэффициент модуляции 20%, а уровень нелинейных искажений 10%, тогда получим значение для амплитуды модулирующего напряжения равного:

,             (4.18)

Затем, используя выражение (4.11), выражаем и находим Е₀, которое задаёт требования к передающему устройству (его место положение, расстояние, мощность и т.п.). Эти требования выбираются согласно (4.4). В нашем случае Е₀»1,34(В).

Исходя из анализа, проведённого в этом разделе, можно сделать следующие выводы:

Ø использовать полупроводниковый диод в качестве нелинейного элемента в отражателе – модуляторе с энергетической точки зрения выгодно, что связано с незначительными энергетическими затратами на источник смещения (Р_СМ» 0,3мВт) и на источник модулирующего напряжения (Р_МОД» 0,2мВт);

Ø увеличение коэффициента модуляции за счёт уменьшения уровня зондируемого сигнала, повлечёт за собой уменьшение уровня отражённого сигнала, что в некоторых случаях недопустимо;

Ø увеличение коэффициента модуляции за счёт увеличения амплитуды модулирующего напряжения приведёт к прямо пропорциональному увеличению уровня нелинейных искажений;

Ø произведение требуемой мощности и коэффициента направленного действия зондирующей антенны должно быть порядка десятков тысяч для расстояния порядка сотни метров;

В разделе приведена примерная методика расчёта отражателя-модулятора, некоторые её этапы могут быть выполнены другими методами и в другом порядке.

 

1234	Поделиться:

Воспользуйтесь поиском по сайту: