 |
Полярная система координат
|
|
|
|
П. 4. 1. Системы координат
1) Декартова система координат. (см. стр.28-29 лекции 4)
Существуют различные способы задания точек набором координат. Аналитическая геометрия опирается на простейшую систему координат — прямоугольную, которая известна из школьного курса математики. Существуют системы координат более общего вида, в которой оси координат могут находиться по отношению друг к другу под произвольным углом. Прямоугольная система координат будет частным случаем, когда углы между осями координат будут прямыми.
Назовем декартовой (аффинной) системой координат пару, состоящую из фиксированной точки O и некоторого базиса. Соответственно трем пространствам  получаем три варианта декартовой системы координат: на прямой, на плоскости и в пространстве. Декартовыми (аффинными) координатами произвольной точки M являются координаты вектора
получаем три варианта декартовой системы координат: на прямой, на плоскости и в пространстве. Декартовыми (аффинными) координатами произвольной точки M являются координаты вектора  в заданном базисе.
в заданном базисе.

С декартовой системой координат связаны следующие понятия:
- начало (системы) координат — точка O в составе декартовой системы координат;
- репер — базис в составе декартовой системы координат, для векторов которого выбирается общая точка приложения в начале координат;
- оси координат (координатные оси) — прямые, на которых лежат векторы репера, задающие направление на этих прямых. Оси имеют специальные названия (в порядке нумерации): ось абсцисс, ось ординат и ось аппликат. Координаты точки именуются по осям: абс- абсцисса, ордината и аппликата. На плоскости отсутствует ось аппликат, на прямой также нет оси ординат.
- координатные плоскости — плоскости, определяемые парами векторов репера. Понятие используется для декартовой системы координат в пространстве;
|
|
|
- радиус-вектор точки M — вектор  , соединяющий начало координат O с этой точкой.
, соединяющий начало координат O с этой точкой.
Декартову систему координат общего вида часто называют косоугольной системой координат.
Если репер декартовой системы координат является ортонормированным базисом, то такую систему координат называют декартовой прямоугольной системой координат, или просто прямоугольной системой координат, а декартовы координаты точки — ее прямоугольными координатами.
Далее будем использовать в основном прямоугольные системы координат, т.е. будем предполагать, что репер представляет собой ортонормированный базис, причем обязательно правый. Отметим, что базис в 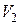 (т.е. на плоскости) называют правым (левым), если первый его вектор совмещается со вторым с помощью кратчайшего поворота против хода (по ходу) часовой стрелки.
(т.е. на плоскости) называют правым (левым), если первый его вектор совмещается со вторым с помощью кратчайшего поворота против хода (по ходу) часовой стрелки.
Итак, под системой координат подразумевается прямоугольная система координат с правым базисом, а под координатами точки — ее прямоугольные координаты. Для обозначения декартовых систем координат, например в пространстве, будем использовать обозначения типа O ijk, где O — начало системы координат, а i, j, k — ортонормированный репер (базис), или Oxyz, где указаны обозначения для координатных осей. 
Полярная система координат

Пример. Найти полярные координаты точки М(-1, -  ).
).

4.2. Преобразование прямоугольных координат (стр. 29-32)
Все прямоугольные системы координат в изучаемом пространстве, вообще говоря, равноправны, т.е. выбор одной из них ничуть не хуже (и не лучше) выбора другой. Те или иные предпочтения отдают исходя из особенностей конкретной задачи. Использование различных систем координат ставит задачу преобразования координат точки, т.е. задачу вычисления ее координат в одной системе координат по ее координатам в другой системе.
Пусть O ijk — некоторая прямоугольная система координат в пространстве, которую мы условно назовем старой, а О 'i'j'k' — вторая прямоугольная система координат, которую будем называть новой (рис. 4.1). Считаем, что известны координаты точки О'( ; b2; b3) и векторов i ' =
; b2; b3) и векторов i ' =  ; j ' = (а12; а22; а32), k '=
; j ' = (а12; а22; а32), k '=  в старой системе координат. Пусть для точки М известны ее координаты (x; y; z) в старой и координаты (х '; y'; z') в новой системах координат. Это значит, что выполняются два равенства
в старой системе координат. Пусть для точки М известны ее координаты (x; y; z) в старой и координаты (х '; y'; z') в новой системах координат. Это значит, что выполняются два равенства 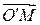 = x' i' + y' j' + z' k',
= x' i' + y' j' + z' k',
|
|
|
 = x i + y j + z k. (4.1)
= x i + y j + z k. (4.1)

|
Векторы  и
и 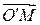 связаны соотношением
связаны соотношением  =
=  +
+ 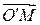 , причем координаты вектора
, причем координаты вектора  являются также координатами начала координат O' новой системы координат относительно старой, т.е.
являются также координатами начала координат O' новой системы координат относительно старой, т.е.  =
=  i + b2 j + b3 k. Поэтому
i + b2 j + b3 k. Поэтому  =
=  +
+ 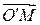 =
=  i + b2 j + b3 k + x ' i' + y' j' + z' k' =
i + b2 j + b3 k + x ' i' + y' j' + z' k' =
=  i + b2 j + b3 k + x '
i + b2 j + b3 k + x ' 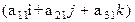 + y'
+ y'  + z'
+ z' 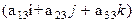 =
=
= ( x ' +
x ' +  y' +
y' +  z' +
z' +  ) i + (
) i + ( x ' +
x ' + 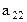 y' +
y' +  z' +
z' + 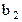 ) j +
) j +
+( x ' +
x ' +  y' +
y' +  z' +
z' +  ) k, (4.2) т.е. получено разложение вектора
) k, (4.2) т.е. получено разложение вектора  в репере старой системы координат. Оно должно совпадать с (4.1) в силу единственности координат вектора в одном и том же базисе. Приравнивая соответствующие коэффициенты разложений в (4.1) и (4.2), получаем
в репере старой системы координат. Оно должно совпадать с (4.1) в силу единственности координат вектора в одном и том же базисе. Приравнивая соответствующие коэффициенты разложений в (4.1) и (4.2), получаем
x =  x ' +
x ' +  y' +
y' +  z' +
z' +  ,
,
y =  x ' +
x ' + 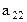 y' +
y' +  z' +
z' + 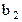 ,
,
z =  x ' +
x ' +  y' +
y' +  z' +
z' +  . (4.3)
. (4.3)
Соотношения (4.3), выражающие старые координаты через новые, представляют собой систему трех линейных уравнений относительно неизвестных x ', y', z'. Чтобы найти новые координаты x', y', z' по известным старым, необходимо решить эту систему относительно новых координат. Система (4.3) при любых x, y, z имеет единственное решение, поскольку ее определитель отличен от нуля. Это следует из того, что выполнены равенства
 = i'j'k'= 1,
= i'j'k'= 1,
так как векторы i', j', k' образуют правый ортонормированный базис и объем построенного на них параллелепипеда равен 1.
Набор коэффициентов в системе (4.3) отражает положение репера новой системы координат, а свободные члены bl, b2, b3 характеризуют изменение начала координат.
Если репер системы координат не изменился, а поменялось лишь начало координат, то формулы преобразования выглядят более просто:
x = x ' + bl,
y = y' + 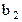 , (4.4)
, (4.4)
z = z' +  .
.
Преобразование (4.4) называют параллельным переносом системы координат в пространстве на вектор  .Все вышеизложенное относится к прямоугольной системе координат в пространстве. Прямоугольная система координат на плоскости отличается от пространственной лишь тем, что репер состоит из двух векторов, а точки имеют всего две координаты. Преобразование системы координат на плоскости описывается уравнениями:
.Все вышеизложенное относится к прямоугольной системе координат в пространстве. Прямоугольная система координат на плоскости отличается от пространственной лишь тем, что репер состоит из двух векторов, а точки имеют всего две координаты. Преобразование системы координат на плоскости описывается уравнениями:
|
|
|
x = all x ' + al2y' + bl,
y =  x ' +
x ' + 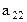 y' +
y' + 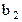 ,
,
где (ali; a2i), i = 1,2, — координаты векторов i', j' нового репера относительно старого (i, j); (bl; b2) — координаты точки O' начала новой системы координат в старой системе координат.
Преобразование параллельного переноса системы координат на плоскости выглядит так:
x = x' + bl,
y =y'+ 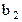 .
.
Если начала новой и старой систем координат на плоскости совпадают, а изменяется лишь репер системы координат, то формулы преобразования координат имеют вид:
x = all x ' + al2y',
y =  x ' +
x ' + 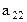 y'. (4.6)
y'. (4.6)
 |
Здесь возможны два случая. В первом из них новый репер может быть получен из старого поворотом последнего на некоторый угол
 вокруг общего начала систем координат, причем полагают, что
вокруг общего начала систем координат, причем полагают, что  > 0 (
> 0 ( < 0) при повороте против хода (по ходу) часовой стрелки. В этом случае преобразование (4.6) называют поворотом системы координат на плоскости на угол
< 0) при повороте против хода (по ходу) часовой стрелки. В этом случае преобразование (4.6) называют поворотом системы координат на плоскости на угол  . Из рис.4.2 следует, что координаты векторов i/ и j/ нового репера относительно старого выражаются через угол поворота
. Из рис.4.2 следует, что координаты векторов i/ и j/ нового репера относительно старого выражаются через угол поворота  :
:
i/ = (cos  ; sin
; sin  ), j/ = (— sin
), j/ = (— sin  ; cos
; cos  ).
).
Зная координаты векторов нового репера относительно старого, мы можем записать уравнения для поворота системы координат на плоскости:
х = х/ cos  - у/sin φ
- у/sin φ
у = х/ sin  + у/ cos
+ у/ cos  . (4.7)
. (4.7)
Если преобразование состоит в последовательном выполнении поворота и параллельного переноса, то оно имеет вид:
 х = х / cos
х = х / cos  - у/ sin φ + b 1
- у/ sin φ + b 1
у = х/ sin  + у/ cos
+ у/ cos  + b2.
+ b2.
Система (4.8) легко решается относительно х/, у/, и обратное преобразование координат, отражающее переход от новой системы координат к старой, будет иметь вид:
х / = х cos  + у sin
+ у sin  +
+  ,
,
у/ = - х sin  + у cos
+ у cos  +
+ 
где  = b1 cos
= b1 cos  + b2 sin
+ b2 sin  , b'2 = -b1 sin
, b'2 = -b1 sin  + b2 cos
+ b2 cos  . Как видим, старая система координат получается из новой с помощью поворота на тот же угол
. Как видим, старая система координат получается из новой с помощью поворота на тот же угол  , но в противоположную сторону (на угол -
, но в противоположную сторону (на угол -  в положительном направлении), и параллельного переноса (на вектор
в положительном направлении), и параллельного переноса (на вектор  ).
).
Во втором случае с помощью поворота старого репера вокруг начала координат на некоторый угол  можно совместить лишь векторы i и i /, но при этом векторы j и j/ окажутся противоположными и для их совмещения потребуется выполнение преобразования зеркального отражения плоскости относительно первой оси координат.
можно совместить лишь векторы i и i /, но при этом векторы j и j/ окажутся противоположными и для их совмещения потребуется выполнение преобразования зеркального отражения плоскости относительно первой оси координат.
|
|
|
В первом случае два репера имеют одинаковую ориентацию, а во втором
- противоположную.
Аналогичную терминологию используют и для пространства. Если начало новой и старой прямоугольных систем координат в пространстве совпадают и изменяется лишь репер системы координат, то формулы преобразования координат имеют вид:
 (4.9)
(4.9)
Преобразование (4.9) называют поворотом системы координат в пространстве, если реперы новой и старой систем координат имеют одинаковую ориентацию, т.е. являются оба правыми или левыми. Как и в случае плоскости, это связано с тем, что реперы с одинаковой ориентацией можно совмещать с помощью поворотов. Например, можно сначала совместить векторы i и i' с помощью поворота старого репера вокруг вектора i x i', а затем выполнить второй поворот вокруг вектора i' для совмещения повернутого вектора j с вектором j '. При этом векторы k и k ' автоматически совпадут для реперов одной ориентации и будут противоположными для реперов противоположной ориентации. В последнем варианте требуется, как и в случае плоскости, выполнение дополнительного преобразования зеркального отражения (относительно координатной плоскости, определяемой векторами i' и j').
|
|
|
12 |


