 |
Модель динамики ансамбля паровых пузырьков
|
|
|
|
Моделирование стационарного и нестационарного истечения адиабатно вскипающей жидкости из коротких каналов
В работе [1] для анализа процесса нестационарного и стационарного истечения вскипающей жидкости в термодинамически неравновесном приближении использован нетрадиционный подход, в основу которого положена разработанная ранее модель, описывающая эволюцию ансамбля паровых пузырьков в процессе их интенсивного роста при быстром понижении внешнего давления /2,3/. Полученная информация положена в основу рассматриваемой здесь математической модели, которая по известным значениям температуры и давления перегретой жидкости на входе в канал истечения, по данным о геометрии канала и по значению давлению газа вне канала, позволяет рассчитать параметры парожидкостного потока пузырьковой структуры в любом сечении канала. Предполагается, что в рамках модели можно уточнить физическую сущность кризиса течения двухфазных потоков и прогнозировать критические параметры потока.
Принципиальным отличием модели является строгое выполнение условий термодинамической неравновесности. И температура и давление в жидкой и паровой фазах внутри канала различны, что позволяет рассмотреть как инерционную, так и термическую стадии роста пузырьков. В данной работе истечение вскипающей жидкости рассмотрено в односкоростном приближении. Модель допускает, однако, возможность учета относительного движения дисперсной паровой фазы в направлении движения потока, а также дробления пузырьков вследствие их динамического взаимодействия с окружающей жидкостью.
Модель динамики ансамбля паровых пузырьков
Математическая модель, прогнозирующая поведение ансамбля растущих или схлопывающихся паровых пузырьков, базируется на модели динамики одиночного пузырька. Принципы построения системы обыкновенных дифференциальных уравнений, описывающих динамику сферического парового пузырька в неограниченном объеме несжимаемой вязкой жидкости с учетом основных определяющих факторов, подробно изложены в работе (2). Эти уравнения дают возможность рассчитать радиус пузырька r(t), давление и радиальную скорость жидкости на границе с пузырьком, соответственно, pr(t) = Pl(R, t) и wR(t) = wi(r, t), а также распределение скорости wl(r, t) и давления Pl(r, t) в окрестности пузырька. Кроме того, рассчитывается изменение температуры Tv(t), плотности rv(t) и давления пара pv(t) внутри пузырька. Предполагается, что эти параметры распределены в пузырьке однородно. Поток теплоты q(t) и массы j(t) через стенку пузырька в процессе испарения и конденсации пара описывается в приближении молекулярно -кинетической теории с учетом скачка температуры на межфазной границе DT = Ts — Tv, так что в общем случае температура жидкости на границе с пузырьком Ts отлична от температуры пара в пузырьке Tv. Распределение температуры в жидкости в окрестности пузырька Tl (r, t) в процессе его роста или сжатия рассматривается в терминах интегрального метода, в рамках которого получено дифференциальное уравнение изменения толщины теплового пограничного слоя в жидкой фазе. В работе (2) приведены также полуэмпирические уравнения, которые с достаточно высокой точностью аппроксимируют температурные зависимости таких теплофизических параметров воды и водяного пара, как скрытая теплота испарения, поверхностное натяжение, плотность насыщенного пара, плотность и вязкость жидкости для всего температурного интервала существования жидкой фазы вплоть до Тсr. Достоверность модели подтверждается удовлетворительным согласием полученных с ее помощью расчетных результатов с известными в литературе экспериментальными данными по росту и схлопыванию одиночных паровых пузырьков в воде в широком интервале изменения режимных параметров.
|
|
|
|
|
|
Уравнения динамики одиночного пузырька положены в основу модели эволюции неограниченного монодисперсного ансамбля паровых пузырьков, которая учитывает динамическое взаимодействие пузырьков и их коллективное влияние на характер микротечений в межпузырьковом пространстве. Кроме основных уравнений динамики одиночного пузырька система уравнений, описывающих поведение ансамбля, включает дифференциальное уравнение для расчета средней температуры жидкости 
, которая не остается постоянной благодаря интенсивному испарению при формировании паровой фазы. Модель динамики пузырьков в ансамбле подробно рассматривается в работе (3). Предполагается, что динамическое развитие пузырьков в ансамбле обусловлено нарушением термодинамического равновесия вследствие быстрого изменения внешнего давления.
Поведение пузырьков в ансамбле рассматривается в приближении ячеечной модели, основные положения которой изложены, например, в работе [4]. Весь объем жидкости в монодисперсном пузырьковом ансамбле разбивается на идентичные сферические ячейки, в центре которых находятся сферические пузырьки. Радиус ячейки x связан с величиной текущего паросодержания b соотношением x= R • b-0.33.Распределение давления зависит от текущих значений размера пузырьков и скорости их роста, а также от количества пузырьков в единице массы Nb, которое в отсутствие коагуляции или дробления пузырьков остается неизменным.
При заданной концентрации Nb величина объемного паросодержания определяется выражением
(1)
Для анализа поведения ансамбля в целом достаточно рассмотреть ситуацию в отдельной ячейке. При росте пузырька в его окрестности в пределах R ≤ r ≤x появляется сферически-симметричное распределение давления
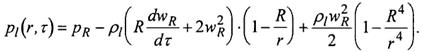(2)
Подстановка в (2) значения 
дает возможность найти давление в жидкости на внешней границе ячейки.
Когда пузырек находится в окружении других растущих пузырьков, поля давления ближайших соседей взаимно перекрываются и давление в любой точке межпузырькового пространства будет превышать внешнее давление, инициирующее рост или сжатие пузырьков. Поэтому поведение каждого отдельного пузырька в таком ансамбле должно определяться не внешним давлением рeх, действующим на систему в целом, а некоторым средним давлением в межпузырьковом пространстве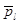 
> рeх. Как и для одиночного пузырька,в бесконечном объеме скорость радиального движения
|
|
|
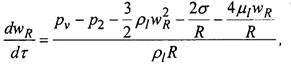(3)
за тем исключением, что в данном случае значение Р2 в (3) определяет не внешнее давление рeх, инициирующее рост пузырьков, а среднее давление в межпузырьковом объеме ансамбля pl (t). Это среднее давление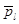 
вычисляется путем интегрирования функции Pl(r,t) по объему жидкости в ячейке и последующего деления на этот объем. Интегрирование правой части (2) приводит к уравнению
где рс определяет значение 
на предыдущем временном шаге расчета.
Усреднение относится как к отдельной элементарной ячейке, так и ко всему объему жидкости в пределах ансамбля. При использовании системы уравнений динамики одиночного пузырька это усредненное давление на каждом очередном шаге расчета определяет скорость изменения радиуса пузырька и значения теплофизических параметров системы, которые, в свою очередь, определяют на последующем шаге новое распределение давления в пределах ячейки и новое значение среднего давления в жидкости. Если термодинамическое равновесие в жидкости с пузырьками внезапно нарушено, например, вследствие резкого падения внешнего давления, наблюдается интенсивный рост паровой фазы. В начальный момент скорость расширения всех пузырьков определяется значением внешнего давления рex, а характер дальнейшего роста пузырьков ансамбля зависит от последующего изменения среднего давления .В результате давление в жидкой фазе асимптотически приближается к значению давления насыщения при данной температуре жидкости, но всегда остается меньше текущего давления пара внутри пузырька pv.
|
|
|
Поведение отдельного пузырька внутри ансамбля при тождественных условиях отличается от поведения одиночного пузырька в бесконечном объеме жидкости тем заметнее, чем сильнее проявляется фактор неодиночности пузырьков, т.е. чем выше концентрация Nb. На рис.1 показано, как меняются во времени среднее давление в межпузырьковом пространстве ансамбля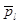 
и скорость расширения пузырьков после мгновенного сброса внешнего давления от начального равновесного значения Рi0 = Psat(Tlo) — 2s/R до величины рex<plo. Среднее давление в жидкости быстро возрастает, приближаясь затем постепенно к значению Psat(Tl). Давление 
стабилизируется тем быстрее, чем выше Nb. При больших концентрациях квазиравновесное давление со временем постепенно понижается по мере роста пузырьков в ансамбле, что объясняется постепенным охлаждением жидкости и уменьшением величины Psat(Tl). Различие в окружающем давлении 
обусловливает различие скоростей роста пузырьков в ансамбле при различных концентрациях, что видно из рисунка. При любых значениях Nb скорость расширения поверхности, одинаково высокая в начальной стадии, очень быстро падает и затем медленно уменьшается, так что со временем скорость роста пузырьков перестает зависеть от их концентрации и скорости роста пузырьков в ансамбле (штрихпунктир) при резком сбросе среднего давления.
Рис.1.Изменение среднего давления в жидкой фазе (сплошная линия)
Расчеты, выполненные в рамках этой модели, показывают, что вид функции (t) практически не зависит от начального радиуса паровых зародышей r0. Различие в начальном размере зародышей (в интервале r0 от 5 до 50 мкм) проявляется лишь на начальной стадии процесса роста пузырьков. Столь же малое влияние на динамику роста пузырьков при одних и тех же значениях Tl0 и Nb оказывает величина сброса внешнего давления, или степень начального перегрева жидкости (3). Однако в короткой начальной стадии роста до установления квазиравновесного значения давления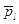 
интенсивность расширения пузырьков тем выше, чем больше перепад внешнего давления. Вместе с тем быстрый рост пузырьков в начальной стадии приводит к более быстрому нарастанию давления внутри ячейки, что, в свою очередь, снижает интенсивность последующего расширения.
Динамика пузырьков в ансамбле и поведение ансамбля в целом определяются разностью текущих значений давления пара в пузырьке pv и среднего давления в жидкости 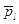. Давление в паровой фазе pv¥pv* Tv обусловлено двумя конкурирующими факторами: с одной стороны, уменьшением плотности и температуры пара из-за увеличения объема пузырька и, с другой - повышением плотности и температуры пара вследствие испарения внутрь пузырька и теплоподвода со стороны жидкости. Корректный учет этих факторов возможен только в предположении различия давления и температуры в жидкой и паровой фазах. Детальное рассмотрение кинетики фазовых переходов и взаимосвязанных процессов тепло- и массопереноса дает возможность прогнозировать эволюцию пузырькового ансамбля и рассчитывать временные зависимости величин R, wr,b, ,Tl и других параметров.
|
|
|
|
|
|
