 |
Выбор векторного критерия качества замкнутой системы из пяти компонентов
|
|
|
|
Выберем пять критериев качества для замкнутой системы:
Выберем следующие пять критериев для оценки качества системы:
1) Время регулирования (время, когда колебания регулируемой величины перестают превышать 5 % от установившегося значения).
2) Время нарастания (время, за которое уровень сигнала меняется с 10% до 90% максимальной амплитуды).
3) Время от начала процесса до первого момента достижения установившегося значения.
4) Перерегулирование ((определяется величиной первого выброса) — отношение разности максимального значения переходной характеристики и ее установившегося значения к величине установившегося значения. Измеряется в процентах).
1)
5) Максимальный отклик (максимальная величина отклика на воздействие).
Выпишем значения по каждому критерию для 5 воздействий (5 графиков), и 2 генераторов.
1 график
1 генератор
5.22 1.14 2.76 8.15 -5.96
2 генератор
11.6 0.936 3.07 37.8 -13.5
2 график
1 генератор
6.83 0 1.68 42.1 -1.21
2 генератор
14.3 0 2.23 11.1 -5.31
3 график
1 генератор
4.04 1.89 3.54 3.45 -21.5
2 генератор
12.2 0.988 3.73 48 -43.5
4 график
1 генератор
4.49 0.798 2.37 28.3 -18.9
2 генератор
14 0.686 3.07 148 -32.8
5 график
1 генератор
7.08 0.11 0.598 103 -12.4
2 генератор
14.6 0.458 2.48 415 -20.9
Таким образом, получим два вектора для двух генераторов:
vect1=[5.22 1.14 2.76 8.15 -5.96 6.83 0 1.68 42.1 -1.21 4.02 1.89 3.54 3.45 -21.5 4.49 0.798 2.37 28.3 -18.9 7.08 0.11 0.598 103 -12.4]
vect2=[11.6 0.936 3.07 37.8 -13.5 14.3 0 2.23 11.1 -5.31 12.2 0.988 3.73 48 -43.5 14 0.686 3.07 148 -32.8 14.6 0.458 2.48 415 -20.9]
Для централизованной системы были получены два аналогичных вектора:
vect1=[4.76 2.78 7.22 0.158 -0.5 6.94 0 1.83 51.2 -1.9 5.29 3 14 0.01 -15.7 5.29 1.62 2.89 8.03 -15.7 6.05 0.277 1.97 43 -11.7];
vect2=[14.8 0.42 3.09 139 -19.1 15.5 0 2.4 4 -10.6 6.44 3.13 7.41 1.11 -33 9.47 1.16 4.44 12.6 -31.7 13.4 0.491 1.43 69.4 -20.3].
8. Сравнение двух вариантов системы (централизованной и децентрализованной) с использованием:
|
|
|
Векторные методы оптимизации (количественные методы выбора наилучшей альтернативы)
При появлении многокритериальных задач возникли дополнительные трудности их решения, связанные с получением информации от ЛПР [4]. Естественной реакцией на это было стремление получить такую информацию сразу и быстро устранить многокритериальность. Этот подход был реализован путем объединения многих критериев в один с помощью так называемых весовых коэффициентов важности критериев. Глобальный критерий вычисляется по формуле:
,
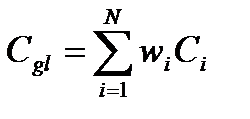где 
-частные критерии, а 
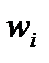- веса критериев.
Определим оценки весов по численной шкале 1-100 для пяти критериев:
1) Время регулирования - 
.
2) Время нарастания -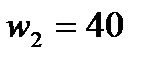 
.
3) Время от начала процесса до первого момента достижения установившегося значения - 
.
4) Перерегулирование -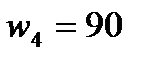 
.
2)
5) Максимальный отклик -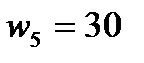 
.
Нормируем дынные оценки весов, разделив каждый вес на сумму всех:
.
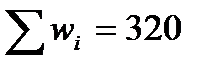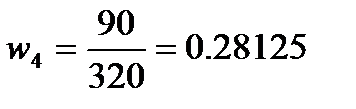
Теперь умножим полученные веса на каждый соответствующий критерий и просуммируем полученные числа:
w=[0.28125 0.125 0.21875 0.28125 0.09375 0.28125 0.125 0.21875 0.28125 0.09375 0.28125 0.125 0.21875 0.28125 0.09375 0.28125 0.125 0.21875 0.28125 0.09375 0.28125 0.125 0.21875 0.28125 0.09375]
vect1=[5.22; 1.14; 2.76; 8.15; -5.96; 6.83; 0; 1.68; 42.1; -1.21; 4.02; 1.89; 3.54; 3.45; -21.5; 4.49; 0.798; 2.37; 28.3; -18.9; 7.08; 0.11; 0.598; 103; -12.4]
vect2=[11.6; 0.936; 3.07; 37.8; -13.5; 14.3; 0; 2.23; 11.1; -5.31; 12.2; 0.988; 3.73; 48; -43.5; 14; 0.686; 3.07; 148; -32.8; 14.6; 0.458; 2.48; 415; -20.9]
vect11=[4.76; 2.78; 7.22; 0.158; -0.5; 6.94; 0; 1.83; 51.2; -1.9; 5.29; 3 14; 0.01; -15.7; 5.29;1.62; 2.89;8.03; -15.7;6.05; 0.277; 1.97;43; -11.7];
vect21=[14.8; 0.42; 3.09; 139;-19.1; 15.5;0;2.4;4;-10.6; 6.44;3.13; 7.41;1.11; -33;9.47; 1.16;4.44;12.6;-31.7;13.4;0.491; 1.43;69.4; -20.3].
kr1=w*vect1
kr11=w*vect11
kr2=w*vect2
kr21=w*vect21
Для первого генератора получили:
Для децентрализованной системы:
kr1 = 57.0699
Для централизованной системы:
kr11 = 39.5666
Для второго генератора получили:
Для децентрализованной системы:
kr2 = 197.0532
Для централизованной системы:
kr21 = 74.3617
Для двух генераторов оценки для централизованной системы получились меньше, что свидетельствует о более качественной централизованной системе (так как все оценки чем больше, тем хуже качество системы).
|
|
|
Вербальные методы анализа
Метод ЗАПРОС.
Метод Замкнутых Процедур Опорных Ситуаций применяется для упорядочения многокритериальных альтернатив [4].
Постановка задачи.
Дано:
1) 
- множество критериев с порядковыми шкалами.
2) 
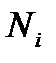- число оценок по шкале критерия 
.
3) 
- шкала критерия 
, 
- вербальные оценки по критерию.
4) 
- множество векторных оценок вида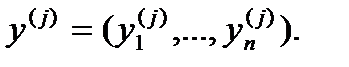 
5) 
- множество векторных оценок, описывающих реальные альтернативы.
Требуется: построить упорядочение многокритериальных альтернатив (множества А) на основе предпочтения ЛПР.
Таким образом, есть 2 альтернативы – централизованная и децентрализованная система (для 1 и для 2 генератора).
Векторные критерии для децентрализованной системы:
vect1=[5.22 1.14 2.76 8.15 -5.96 6.83 0 1.68 42.1 -1.21 4.02 1.89 3.54 3.45 -21.5 4.49 0.798 2.37 28.3 -18.9 7.08 0.11 0.598 103 -12.4]
vect2=[11.6 0.936 3.07 37.8 -13.5 14.3 0 2.23 11.1 -5.31 12.2 0.988 3.73 48 -43.5 14 0.686 3.07 148 -32.8 14.6 0.458 2.48 415 -20.9]
Векторные критерии для централизованной системы:
vect1=[4.76 2.78 7.22 0.158 -0.5 6.94 0 1.83 51.2 -1.9 5.29 3 14 0.01 -15.7 5.29 1.62 2.89 8.03 -15.7 6.05 0.277 1.97 43 -11.7];
vect2=[14.8 0.42 3.09 139 -19.1 15.5 0 2.4 4 -10.6 6.44 3.13 7.41 1.11 -33 9.47 1.16 4.44 12.6 -31.7 13.4 0.491 1.43 69.4 -20.3].
Было выделено 5 критериев оценки систем:
1) Время регулирования.
2) Время нарастания.
3) Время от начала процесса до первого момента достижения установившегося значения.
4) Перерегулирование.
3)
5) Максимальный отклик.
Время регулирования (f1). Шкала состоит из 2-х оценок (N1=2):
1) маленький промежуток времени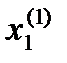 
2) большой промежуток времени 
Время нарастания (f2). Шкала состоит из 2-х оценок (N2=2):
1) маленький промежуток времени 
2) большой промежуток времени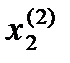 
Время от начала процесса до первого момента достижения установившегося значения. (f3). Шкала состоит из 2-х оценок (N3=2):
1) маленький промежуток времени 
2) большой промежуток времени 
Перерегулирование. (f4). Шкала состоит из 2-х оценок (N4=2):
1) маленькое 
2) высокое 
Максимальный отклик. (f5). Шкала состоит из 2-х оценок (N5=2):
1) маленький 
2) высокий 
Множество A будет состоять из векторных оценок сравниваемых проектов, например: a(i) = (маленький промежуток времени, большой промежуток времени, большой промежуток времени, маленькое, высокий).
|
|
|
Метод ЗАПРОС в данном случае может быть применен для упорядочивания сравниваемых вариантов по предпочтительности с учетом заданных критериев, после чего уже будет осуществлен отбор наиболее предпочтительной системы/
Основная идея метода ЗАПРОС заключается в том, что ЛПР предлагается сравнивать не реальные альтернативы (векторные оценки из множества A), а некоторые гипотетические варианты (их векторные оценки из множества Y).
Заданы пять критериев, у каждого шкала с двумя оценками.
Построим оценки для всех пяти графиков.
У первой альтернативы список векторных оценок будет иметь вид:
Для 1 генератора:
L11 = { (1,0,1,0,0),(1,1,1,0,1),(0,1,0,0,0),(0,1,0,0,0),(0,0,1,0,0) }.
Для 2 генератора:
L12 = { (1,0,0,1,0),(0,0,0,0,0),(0,1,1,0,1),(0,1,0,0,1),(1,0,0,0,1) }.
У второй альтернативы:
Для 1 генератора:
L21 = { (1,1,0,1,1),(1,1,1,0,1),(0,0,1,1,1),(0,0,0,1,0),(0,0,0,1,0) }.
Для 2 генератора:
L22 = { (1,1,0,0,0),(0,0,0,1,1),(1,0,0,1,1),(1,0,0,1,1),(1,0,1,1,1) }.
Представим полученные оценки в виде:
L = {(оценки по 1 критерию),(оценки по 2 критерию),(оценки по 3 критерию),(оценки по 4 критерию),(оценки по 5 критерию) }.
У первой альтернативы список векторных оценок будет иметь вид:
Для 1 генератора:
L11 = { (1,1,0,0,0),(0,1,1,1,0),(1,1,0,0,1),(0,0,0,0,0),(0,1,0,0,0) }.
Для 2 генератора:
L12 = { (1,0,0,0,1),(0,0,1,1,0),(0,0,1,0,0),(1,0,0,0,0),(0,0,1,1,1) }.
У второй альтернативы:
Для 1 генератора:
L21 = { (1,1,0,0,0),(1.1,0,0,0,),(0,1,1,0,0),(1,0,1,1,1),(1,1,1,0,0) }.
Для 2 генератора:
L22 = { (1,0,1,1,1),(1,0,0,0,0),(0,0,0,0,1),(0,1,1,1,1),(0,1,1,1,1) }.
Данные можно объединить в общий критерий (1 для 5 графиков).
У первой альтернативы список векторных оценок будет иметь вид:
Для 1 генератора:
L11 = { 0,1,1,0,0 }.
Для 2 генератора:
L12 = { 0,0,0,0,1 }.
У второй альтернативы:
Для 1 генератора:
L21 = { 0,0,0,1,1 }.
Для 2 генератора:
L22 = { 1,0,0,1,1 }.
Полученные пары предъявляются ЛПР для сравнения.
Будем задавать вопросы, подобные этим:
Вопрос. Что вы предпочитаете: систему с большим временем регулирования или большим временем нарастания?
Ответ ЛПР. Систему с большим временем нарастания.
Вопрос. Что вы предпочитаете: систему с большим временем нарастания или большим перерегулированием?
Ответ ЛПР. Систему с большим временем нарастания.
Пусть АБВГД – оценки по критериям.
|
|
|
А1Б1В1Г1Д1 – оценки для первой альтернативы.
А2Б2В2Г2Д2 – оценки для второй альтернативы.
Будем сравнивать оценки попарно, выступая в роли ЛПР.
Для первого генератора:
АБ -> Б1 (то есть выбираем из А1, Б1, А2,Б2)
АВ -> В1
АГ -> Г2
АД -> Д2
БВ-> Б1
БГ-> Г2
БД -> Д2
ВГ-> Г2
ВД-> Д2
ГД-> Д2
Таким образом, выберем наилучшие оценки - Г2, Д2, из чего следует, что вторая альтернатива (централизованная система для 1 генератора) лучше.
Для второго генератора:
АБ -> A2
АВ -> A2
АГ -> А2
АД -> А2
БВ-> Б1
БГ-> Г2
БД -> Д2
ВГ-> Г2
ВД-> Д2
ГД-> Г1
Таким образом, выберем наилучшие оценки - А2, Г2, Д2, из чего следует, что вторая альтернатива (централизованная система для 2 генератора) лучше.
ЗАКЛЮЧЕНИЕ
В результате выполненной работы была исследована модель турбоагрегата, состоящая из двух параллельно работающих синхронных генераторов, а именно было проделано следующее:
ü декомпозиция системы на подсистемы,
ü проведена проверка управляемости подсистемы (система управляема),
ü сформирована замкнутая система,
ü построена система сравнения для замкнутой подсистемы,
ü система сравнения была проверена на устойчивость (система сравнения неустойчива),
ü построены переходные процессы,
ü выбран векторный критерий качества замкнутой системы из пять составляющих,
ü проведено сравнение двух вариантов системы (централизованная и децентрализованная) с использованием векторных методов оптимизации и вербальных методов анализа (по двум методам централизованная система получилась лучше).
Список литературы
1. Шашихин В.Н. Теория автоматического управления. Методы декомпозиции, агрегирования и координации. Учеб. пособие. СПб.: Изд-во Политехн. ун-та, 2004. 116 с.
2. Козлов В.Н., Куприянов В.Е., Шашихин В.Н. Управление энергетическими системами. Часть 1:Теория автоматического управления: Учеб. пособие. – СПб.: Изд-во Политехн. ун-та, 2006.
3. Козлов В.Н., Куприянов В.Е., Шашихин В.Н. Теория автоматического управления: Учеб. пособие. – СПб.: Изд-во Политехн. ун-та, 2008.
4. Ларичев О. И. Теория и методы принятия решений, а Также Хроника событий в Волшебных Странах: Учебник. - М.: Логос, 2000. -296 с.
ПРИЛОЖЕНИЕ
%% система 5*5
A_n=[0 1 0 0 0;-7.8 -0.168 30 0 0; 0 0 -0.9 0.6 0; 0 -0.016 0 -0.9 0.6;0 0 0 0 -0.9];
A_v=[0 1 0 0 0;-5.2 -0.112 45 0 0; 0 0 -0.6 0.9 0; 0 -0.016 0 -0.6 0.9;0 0 0 0 -0.6];
B=[0;0;0;0;0.75];
%% система 10*10
format short g
Nl=[0;0;0;0;0]
B10=[B Nl;Nl B];
Nl2=[0 0 0 0 0]
A_21_n=[0 0 0 0 0; 0.8 0 0 0 0; 0 0 0 0 0; 0 0 0 0 0;0 0 0 0 0];
A_21_v=[0 0 0 0 0; 1.2 0 0 0 0; 0 0 0 0 0; 0 0 0 0 0;0 0 0 0 0];
A10_n=[A_n A_21_n; A_21_n A_n];
A10_v=[A_v A_21_v; A_21_v A_v];
%% медианные матрицы А и A11
for i=1:1:10
for j=1:1:10
A10_med(i,j)=[A10_n(i,j)+A10_v(i,j)]/2;
end
end
for i=1:1:5
|
|
|
for j=1:1:5
A_med(i,j)=[A_n(i,j)+A_v(i,j)]/2;
end
end
%% собственные числа медианных матриц
eig(A_med)
sob_chA10=eig(A10_med);
%% матрица управляемости, ее ранг
Sy=[B A_med*B A_med^2*B A_med^3*B A_med^4*B]
rang=rank(Sy)
%% решим уравнение Ляпунова:
Q=eye(5);
X=lyap((A_med)',A_med,Q)
%% находим макс и мин собственные числа матриц Q и Ляпунова
lam_X=eig(X)
lam_Q=eig(Q)
min_lamX= 0.38056
max_lamX= 1250.3
min_lamQ= 1
A_21=[0 0 0 0 0; 1 0 0 0 0; 0 0 0 0 0; 0 0 0 0 0;0 0 0 0 0];
A_12=A_21;
lamA=eig(A_21'*A_21)
max_lamA=1
%% находим элементы матрицы W для системы сравнения
w11=-0.5*min_lamQ/max_lamX;
w22=w11;
w21=max_lamX*sqrt(max_lamA)/(sqrt(min_lamX)*sqrt(min_lamX));
w12=w21;
format long g
W=[w11 w12;w21 w22]
%% находим соб. числа матрицы W для системы сравнения
eigW=eig(W)
%% находим элементы матрицы Gamma для системы сравнения
lam_B=eig(B'*B);
gamma11=max_lamX*sqrt(lam_B)/sqrt(min_lamX);
gamma22=gamma11;
Gamma=[gamma11 0;0 gamma22]
%% Решение уравнения Риккати
Q=eye(5)
R=1
[K,P,Lam]=lqr(A_n,B,Q,R)
[K2,P2,Lam2]=lqr(A_v,B,Q,R)
K10_n=[K Nl2; Nl2 K]
K10_v=[K2 Nl2; Nl2 K2]
for i=1:1:2
for j=1:1:10
K10_med(i,j)=[K10_n(i,j)+K10_v(i,j)]/2;
end
end
%% Построение системы сравнения
Az_n=A10_n-B10*K10_med
Az_v=A10_v-B10*K10_med
for i=1:1:10
for j=1:1:10
Az_med(i,j)=[Az_n(i,j)+Az_v(i,j)]/2;
end
end
RRR=rank(Az_med)
%% построение переходных процессов
%
C1=[1 0 0 0 0];
C2=[0 1 0 0 0];
C3=[0 0 1 0 0];
C4=[0 0 0 1 0];
C5=[0 0 0 0 1];
C11=[C1 Nl2];
C21=[C2 Nl2];
C31=[C3 Nl2];
C41=[C4 Nl2];
C51=[C5 Nl2];
D=0;
sys11=ss(Az_n,B10,C11,D);
sys21=ss(Az_v,B10,C11,D);
sys31=ss(Az_med,B10,C11,D);
sys12=ss(Az_n,B10,C21,D);
sys22=ss(Az_v,B10,C21,D);
sys32=ss(Az_med,B10,C21,D);
sys13=ss(Az_n,B10,C31,D);
sys23=ss(Az_v,B10,C31,D);
sys33=ss(Az_med,B10,C31,D);
sys14=ss(Az_n,B10,C41,D);
sys24=ss(Az_v,B10,C41,D);
sys34=ss(Az_med,B10,C41,D);
sys15=ss(Az_n,B10,C51,D);
sys25=ss(Az_v,B10,C51,D);
sys35=ss(Az_med,B10,C51,D);
% step(sys11,20)
% hold on
% step(sys21,20)
% hold on
% step(sys31,20)
% hold on
% step(sys12,20)
% hold on
% step(sys22,20)
% grid on
% step(sys32,20)
% hold on
% step(sys13,20)
% hold on
% step(sys23,20)
% hold on
% step(sys33,20)
% hold on
% step(sys14,20)
% hold on
% step(sys24,20)
% hold on
% step(sys34,20)
% hold on
% step(sys15,20)
% hold on
% step(sys25,20)
% hold on
% step(sys35,20)
% grid on
%% построение АЧХ
% nyquist(sys35)
%% Векторные критерии для двух систем с двумя генераторами
w=[0.28125 0.125 0.21875 0.28125 0.09375 0.28125 0.125 0.21875 0.28125 0.09375 0.28125 0.125 0.21875 0.28125 0.09375 0.28125 0.125 0.21875 0.28125 0.09375 0.28125 0.125 0.21875 0.28125 0.09375]
vect1=[5.22; 1.14; 2.76; 8.15; -5.96; 6.83; 0; 1.68; 42.1; -1.21; 4.02; 1.89; 3.54; 3.45; -21.5; 4.49; 0.798; 2.37; 28.3; -18.9; 7.08; 0.11; 0.598; 103; -12.4]
vect2=[11.6; 0.936; 3.07; 37.8; -13.5; 14.3; 0; 2.23; 11.1; -5.31; 12.2; 0.988; 3.73; 48; -43.5; 14; 0.686; 3.07; 148; -32.8; 14.6; 0.458; 2.48; 415; -20.9]
vect11=[4.76; 2.78; 7.22; 0.158; -0.5; 6.94; 0; 1.83; 51.2; -1.9; 5.29; 3; 14; 0.01; -15.7; 5.29;1.62; 2.89;8.03; -15.7;6.05; 0.277; 1.97;43; -11.7];
vect21=[14.8; 0.42; 3.09; 139;-19.1; 15.5;0;2.4;4;-10.6; 6.44;3.13; 7.41;1.11; -33;9.47; 1.16;4.44;12.6;-31.7;13.4;0.491; 1.43;69.4; -20.3]
kr1=w*vect1
kr11=w*vect11
kr2=w*vect2
kr21=w*vect21
|
|
|
