 |
Случайный процесс с дискретным числом состояний
|
|
|
|
Система Х называется системой с дискретным числом состояний Х 1, Х 2, …, Хn, …, если переход из одного состояния в другое осуществляется скачком. Возможные состояния системы изображаются с помощью так называемого графа состояний, на котором состояния изображены прямоугольниками, а возможные переходы системы из состояния в состояние – стрелками.
На черт. 2 изображен граф системы, имеющей 3 состояния и возможные переходы из Х 1 в Х 2, из Х 1 в Х 3, из Х 3 в Х 2, из Х 3 в Х 1. Состояние Х 2 – состояние без выхода. На черт. 3 изображен граф системы, имеющей четыре состояния.
Для описания случайного процесса, протекающего в системе, используются вероятности состояний p 1(t), p 2(t), …, pn (t), где pk (t) (k = 1, 2, …, n) – вероятности того, что в момент t система находится в состоянии Хk.
Вероятности pk (t) удовлетворяют условию:
.
Пусть переходы системы из одного состояния в другое осуществляются под влиянием простейших потоков событий. В этом случае для вероятностей состояний системы p 1(t), p 2(t), …, pn (t) можно составить систему линейных дифференциальных уравнений. При составлении дифференциальных уравнений удобно пользоваться размеченным графом состояний, на котором у каждой стрелки, ведущей из состояния в состояние, проставлена плотность (интенсивность) потока событий, переводящего из состояния в состояние по данной стрелке (черт. 4).
Здесь li,j обозначает плотность потока событий, переводящего систему из состояния Хi в состояние Хj.
Если имеется размеченный граф состояний системы Х, то систему дифференциальных уравнений для вероятностей pk (t) (k = 1, 2, …, n) можно составить, пользуясь простым правилом. В левой части каждого уравнения стоит 
, а в правой – столько членов, сколько стрелок связано непосредственно с состоянием Хk. Если стрелка ведет в данное состояние, то член имеет знак плюс, если ведет из данного состояния, то член имеет знак минус. Каждый член равен плотности потока событий, переводящего систему по данной стрелке, умноженной на вероятность того состояния, откуда исходит стрелка. Например, для системы Х с размеченным графом (черт. 4) система дифференциальных уравнений будет:
|
|
|
Число уравнений можно уменьшить на 1, если учесть, что p 1(t) + p 2(t) + p 3(t) + p 4(t) = 1.
Начальные условия для интегрирования такой системы отражают состояние системы в начальный момент. Если, например, при t = 0 система была в состоянии pk, то pk (0) = 1; pi (0) = 0, где i ≠ k.
Предельным режимом для системы Х называется случайный процесс, устанавливающийся в системе при t ⇢∞. В этом случае 
. Следовательно, 
. Если число состояний системы конечно, нет состояний без выхода, то предельный режим существует и характеризуется предельными вероятностями p 1, p 2, …, pn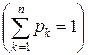 
.
Чтобы найти pk, приравниваем нулю левые части дифференциальных уравнений (полагаем 
= 0) и решаем полученную систему линейных алгебраических уравнений. К ним добавляем нормировочное условие .
Для системы Х предельный режим будет определяться системой алгебраических уравнений
Пример. Известен граф состояний системы:
1) Составить дифференциальные уравнения для вероятностей 
, если известно, что в начальный момент времени система находится в состоянии 
.
2) Для стационарного режима составить систему линейных уравнений и найти предельные вероятности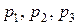 
.
Решение.
1)
.
Начальные условия: 
.
2) Для стационарного режима имеем:
Из системы находим: 
, 
. Подставим в 4-е уравнение: 
, 
, 
.
Заметим, что 1-е уравнение оказалось «лишним». Но его можно использовать для проверки.
СМО с отказами
Работа СМО с отказами определяется следующими параметрами:
|
|
|
1) число каналов n;
2) плотность потока заявок l;
3) плотность «потока обслуживаний» m, то есть плотность потока заявок, обслуживаемых одним непрерывно занятым каналом.
Величина m обратно среднему времени обслуживания одной заявки:
,
где 
= M [ Tоб ]; Tоб – случайное время обслуживания.
Рассмотрим размеченный граф состояний n -канальной СМО с отказами. Состояние Хk (1 ≤ k ≤ n) соответствует занятости ровно К каналов из n.
Отсюда получаем дифференциальные уравнения для вероятностей состояний (уравнения Эрланга):
Эту систему обычно интегрируют при начальных условиях:
P 0(0)=1; pk (0)=0 (k >0)
– в начальный момент все каналы свободны.
При t ® ¥ существует предельный (установившийся, стационарный) режим. В этом случае
то есть система дифференциальных уравнений Эрланга заменяется однородной системой линейных алгебраических уравнений
(3.1)
Последнее уравнение обозначает, что сумма вероятностей всех состояний равна 1.
Начальные условия для стационарного режима не важны: pk не зависят от того, сколько каналов было занято в начальный момент времени.
Решим систему. Из первого уравнения (3.1) имеем
(3.2)
Из второго с учетом (3.2)
(3.3)
Аналогично из третьего с учетом (3.2) и (3.3)
и вообще, для любого k ≤ n
(3.4)
Введем обозначение 
и назовем величину a приведенной плотностью потока заявок. Здесь a – среднее число заявок, приходящееся на среднее время обслуживания одной заявки.
Действительно, 
.
Тогда 
.
Используем формулу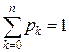 
.
Подставив выражения 
в эту формулу, получим
(3.5)
откуда
(3.5*)
Окончательно для pk получим
(3.6)
где 
, или P (k; a) = R (k; a) – R (k –1; a).
Значения функции R (k; a) могут быть найдены по таблице.
При малых n вероятности pk несложно вычислить непосредственно.
Вероятность того, что заявка будет обслужена (не получит отказа) выражается формулой
(3.7)
Найдем остальные характеристики СМО.
Среднее число занятых каналов 
определим из равенства: m = lРобс, где справа и слева стоит плотность потока обслуженных заявок.
Откуда
(3.8)
или 
Выражение для можно найти и из формулы 
, где pk определены раньше.
Обозначим вероятность того, что произвольно взятый канал занят обслуживанием какой-то заявки, через Рзан. Очевидно, что эта вероятность одинакова для всех каналов, следовательно 
, откуда
|
|
|
(3.9)
Среднее время занятости канала 
, то есть равно среднему времени обслуживания заявки.
Среднее время простоя канала 
определим из условия 
, откуда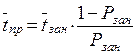 
.
Задача 1. Организация принимает заказы по телефону. Имеется четыре телефонных линии. В среднем за 1 мин. поступает 6 заказов. Время приема заказа в среднем составляет 30 сек. и распределено по показательному закону. Определить:
1) вероятности pk – занято k каналов;
2) вероятность того, что заказ будет принят;
3) среднее число занятых каналов;
4) вероятность занятости канала;
5) среднее время простоя канала.
Имеем СМО с отказами.
Решение. Число каналов n =4;
l = 6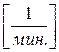 
; 
; 
; 
.
1) Вычислим вероятности pk:
.
Имеем: 
(полагаем 0!=1).
,
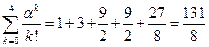откуда 
.
2) Вероятность того, что заказ будет принят, то есть хотя бы один телефон свободен:
робс = 1 – р 4 =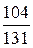 
» 0,793.
3) Среднее число занятых каналов:
.
4) Вероятность того, что произвольно взятый канал будет занят:
.
5) Среднее время простоя канала:
.
Замечание. Среднее число занятых каналов можно вычислить и по формуле:
Задача 2. Рассматривается работа автоматической телефонной станции (АТС), рассчитанной на одновременное обслуживание 25 абонентов (25-канальная СМО). Вызов на АТС поступает в среднем через 6 секунд. Каждый разговор длится в среднем 2 минуты. Если абонент застает АТС занятой, то он получает отказ. Если абонент застает свободным хотя бы один из 25 каналов, то он соединяется с нужным ему номером.
Определить: 1) вероятность обслуживания абонента;
2) среднее число занятых каналов;
3) вероятность того, что произвольно взятый канал будет занят;
4) среднее время простоя канала.
Решение. n =25; l = 
; 
; 
.
1) Вероятность обслуживания:
2) Среднее число занятых каналов:
.
3) Вероятность того, что канал занят:
.
4) Среднее время простоя канала.
.
Из полученных данных видно, что АТС достаточно загружена, но имеется некоторый резерв. Вероятность дозвониться с первого раза достаточная.
Задача 3. Рассмотрим работу телефонной справочной службы с одним каналом обслуживания (СМО с отказом). Среднее число поступающих в течение одного часа заявок равно 20. Среднее время обслуживания одной заявки составляет одну минуту.
|
|
|
Найти основные характеристики СМО:
1) вероятности состояний системы р 0, р 1;
2) вероятность обслуживания заявки робс;
3) среднее число занятых каналов ;
4) вероятность занятости канала;
5) среднее время простоя канала.
Проанализировать, как изменятся характеристики, если создать еще один канал обслуживания. С какой интенсивностью должна обслуживаться заявка каждым каналом, чтобы доля потерянных заявок составила менее 20 %?
Решение.
а) Для одноканальной СМО.
Из условия п = 1; l = 20 (з/час); 
. Найдем 
.
Для нахождения р 0 и р 1 используем формулу: 
Þ 
.
2) робс = 1 – p 1 = 
=0,75.
3) Среднее число занятых каналов 
.
4) Найдем вероятность занятости канала:
(для одноканальной СМО Рзан = р 1).
5) Найдем среднее время простоя канала:
.
б) Для двухканальной СМО с отказом: п = 2; l = 20 (з/час); 
; 
.
1) Состояний системы будет три: р 0, р 1; р 2.
В этом случае 
.
Вычислим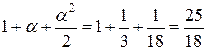 
.
Найдем 
..
2) робс = 1 – p 2 = 
=0,96.
3) 
.
4) 
.
5) 
.
в) Заявка, поступившая в систему, теряется в том случае, если заняты все каналы. В нашем случае р 2 = 0,2. Параметр l = 20 остается, так как не зависит от внутренних характеристик системы. Новую интенсивность обслуживания обозначим m *. Тогда 
; 
. Получим уравнение 
или 2 a *2 – a – =0. Решая полученное уравнение, получим a *1 = 1, a *2 = 
. Так как a * > 0, то a *2 = не удовлетворяет условию задачи. Получим 
; m * = l; m * = 20.
Итак, интенсивность обслуживания, при которой теряется менее 20% заявок, должна быть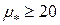 
заявок в час.
Задача 4. Станция ПВО имеет четыре канала наведения. Каждый канал может наводить одну ракету на одну цель. Среднее время наведения 30 сек. Поток целей простейший с плотностью l = 4 цели в минуту. Станцию можно считать системой с отказом, так как цель, по которой наведение не началось в момент, когда она вошла в зону действия станции ПВО, вообще остается не атакованной. Найти следующие характеристики станций:
1) рi – вероятность того, что занято i каналов;
2) робс – вероятность уничтожения цели;
3) вероятность прорыва цели к объекту;
4) – среднее число занятых каналов;
5) с какой интенсивностью должны работать два канала, чтобы доля прорвавшихся через станцию ПВО объектов осталась на прежнем уровне?
Решение. Рассмотрим время в минутах.
Дано: п = 4; 
; l = 4.
Найдем 
; 
.
1) Воспользуемся формулой
.
Найдем 
Следовательно, 
Контроль: 
.
2) Вероятность уничтожения цели:
робс = 1 – p 4 = 1 – 
.
3) Вероятность прорыва цели к объекту равна 
.
4) Среднее число занятых каналов
.
5) Обозначим вероятности состояний двухканальной системы р 0*, р 1*; р 2*.
|
|
|
Пусть m – интенсивность работы канала для двухканальной системы (то есть количество объектов, на которые канал наводит ракету за 1 минуту). Пусть . Поток целей для двухканальной системы остается с прежней плотностью l = 4. Цель прорывается к объекту в случае, если заняты все каналы, то есть p 4 = p 2* или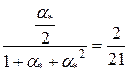 
. После преобразований получим квадратное уравнение 17 a *2 – 4 a * – 4 =0. Решая это уравнение, получим 
не удовлетворяет условиям задачи.
Найдем m * из уравнения ; 
, откуда m * 
.
Сравним результаты. В четырехканальной системе каждый канал за минуту наводил ракеты на 2 цели. В двухканальной системе, которая обладает той же степенью надежности защиты объекта, интенсивность работы канала должны составлять 6,56 целей в минуту, то есть возрасти более чем в три раза.
Задача оптимизации СМО с отказом.
Пусть известна плотность потока поступающих в систему заявок 
, среднее число заявок, обслуживаемых одним каналом в единицу времени 
. За обслуживание одной заявки клиент платит A рублей. Содержание одного канала обслуживания составляет B рублей в час. Необходимо определить оптимальное число каналов таким образом, чтобы получить максимальную прибыль.
Метод решения: 
- среднее число заявок, обслуживаемых системой в единицу времени.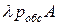 
- денежная сумма, оплаченная клиентами за единицу времени (доходы). 
- расходы на содержание n каналов. Учитывая, что 
, решение задачи сводится к нахождению минимума функции целочисленного аргумента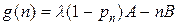 
. Методы дифференциального исчисления здесь не применимы, так как 
не существует. Найдем 
и 
. Если 
, то оптимальное число каналов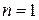 
. Если 
, то найдем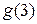 
. Если 
, то оптимальное число каналов 
. В противном случае ищем 
и т.д. до тех пор, пока не получим неравенство 
. В этом случае оптимальное число каналов 
. Задача всегда имеет решение, так как доходы ограничены числом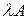 
, а расходы с увеличением n неограниченно увеличиваются. В частности, если расходы заведомо превысят доходы в случае 
Задача 5. Пусть в СМО с отказом поступает в среднем 12 заявок в час. Среднее время обслуживания заявки составляет 10 мин. За обслуживание заявки клиент платит 50 рублей. Содержание одного канала обслуживания обходится 90 рублей в час. Определить число каналов обслуживания, при которых прибыль максимальна.
Решение. Из условия имеем 
, 
Þ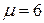 
, 
. Функция прибыли 
1) Пусть .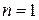 
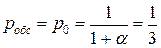. Прибыль 
.
2) Для 
. Прибыль 
. 
, поэтому рассмотрим 
.
3) Для получим 
. Прибыль 
. 
, поэтому рассмотрим 
.
4) Для имеем 
. Прибыль составит 
. Прибыль уменьшилась, так как 
, то оптимальное число каналов обслуживания .
Смо с ожиданием
Если время пребывания в очереди и число мест в очереди не ограничено, то такая система называется чистой системой с ожиданием. Предельный стационарный режим при t ® ¥ существует, если a < n, то есть «мощность» системы достаточна для обслуживания данного потока заявок. В случае a ³ n очередь будет неограниченно расти и предельного стационарного режима не существует. Размеченный граф состояний имеет вид:
где состояния Х 0 – все каналы свободны;
Х 1 – один канал занят;
… … … … … … … …
Хn –1 – n –1 канал занят;
Хn – n каналов занято;
Хn +1 – n каналов занято, и одна заявка стоит в очереди;
Хn + s – n каналов занято и s заявок стоит в очереди.
Предельные вероятности состояний определяются по формулам:
, (4.1)
, (4.2)
или
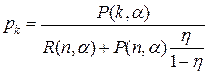, (4.3)
, (4.4)
где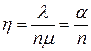 
.
Формулы (4.3) и (4.4) имеет смысл применять при n ³ 5.
Среднее число заявок, находящихся в очереди определяется по формуле
(4.5)
или
(4.6)
В частности, для одноканальной СМО (n =1)
(4.7)
Для двухканальной СМО (n =2) средняя длина очереди определена формулой:
(4.8)
Задача 1. Рассматривается работа автозаправочной станции (АЗС), на которой имеются четыре заправочных колонки (n =4). Заправка одной машины длится в среднем 3 минуты. В среднем на АЗС каждую минуту прибывает машина, нуждающаяся в заправке бензином. Число мест в очереди практически не ограничено. Все машины, вставшие в очередь, терпеливо дожидаются своей очереди, так как на других АЗС города бензина нет.
Определить, существует ли установившийся режим обслуживания; если да, то найти:
1) вероятности p 0, p 1, p 2, p 3, p 4, p 5, p 6;
2) вероятность наличия очереди Роч;
3) среднюю длину очереди 
;
4) среднее число занятых колонок ;
5) вероятность занятости колонки Рзан;
6) среднее время ожидания машины в очереди 
;
7) среднее время простоя колонки.
Решение. 
; n = 4; a < n. Следовательно, стационарный предельный режим при t ® ¥ существует.
1) Вероятности pi:
Используя формулу (4.1), находим
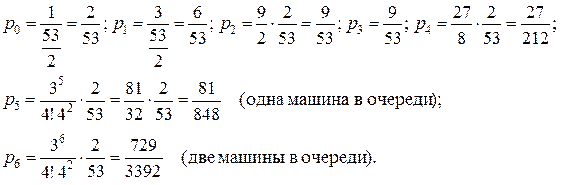
2) Вероятность наличия очереди:
3) Среднее число машин, находящихся в очереди, можно найти по формуле (4.5)
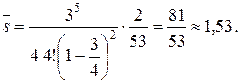
4) Так как Робс = 1, то среднее число занятых колонок
5) Среднее время ожидания машины в очереди:
.
6) Среднее время пребывания машины у АЗС равно 3 + 1,53 = 4,53 мин.
7) Среднее число машин, ожидающих заправки или заправляющихся 
8) Среднее время простоя колонки 
, так как 
.
Задача 2. На вход трехканальной системы с неограниченным временем ожидания поступает простейший поток заявок с плотностью l = 4 (четыре заявки в час). Среднее время обслуживания одной заявки 
Определить, существует ли установившийся режим обслуживания; если да, то найти вероятности состояний p 0, p 1, p 2, p 3; вероятность наличия очереди и среднюю длину очереди .
Решение. Имеем 
, так как 
; ; n = 3; a < n. Значит, стационарный режим существует. По формуле (4.1) находим 
Вероятность наличия очереди роч = 1 – (р 0 + р 1 + р 2 + р 3)» 0,297.
Средняя длина очереди определяется по формуле (4.5) или (4.6): 
|
|
|
