 |
N-каналъная СМО с отказами (задача Эрланга)
|
|
|
|
СИСТЕМЫ МАССОВОГО ОБСЛУЖИВАНИЯ
Одноканальная СМО с отказами
Абсолютная пропускная способность (среднее число заявок, обслуживаемых в единицу времени):
А= 
(шт./ед. времени),
где λ. - интенсивность потока заявок; μ - интенсивность потока обслуживаний.
Относительная пропускная способность (средняя доля заявок, обслуживаемых системой):
Q=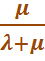 
Вероятность отказа (вероятность того, что заявка покинет СМО необслуженной):
Очевидны следующие соотношения: Q = 1- и 
.
Пример 1. Технологическая система состоит из одного станка. На станок поступают заявки на изготовление деталей в среднем через 0,5 часа. Среднее
время () изготовления одной детали равно 0,6 час. Если при поступлении заявки на изготовление детали станок занят, то она (деталь) направляется на другой станок. Найти абсолютную и относительную пропускную способности системы и вероятность отказа по изготовлению детали.
Решение.
То есть в среднем примерно 46 % деталей обрабатываются на этом станке.
То есть в среднем примерно 54 % деталей направляются на обработку на другие станки.
N-каналъная СМО с отказами (задача Эрланга)
Это одна из первых задач теории массового обслуживания. Она возникла из практических нужд телефонии и была решена в начале XX века датским математиком Эрлангом.
Выходные характеристики (характеристики эффективности) данной СМО определяются следующим образом.
Абсолютная пропускная способность:
где n - количество каналов CMO; 
- вероятность нахождения CMO в начальном состоянии, когда все каналы свободны (финальная вероятность нахождения CMO в состоянии 
).
Для того чтобы написать формулу для определения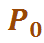 
, рассмотрим рис. 1.
|
|
|
Граф, представленный на этом рисунке, называют еще графом состояний для схемы «гибели и размножения». Напишем сначала для 
общую формулу (без доказательства):
Кстати, остальные финальные вероятности состояний СМО запишутся следующим образом:
1) Вероятность того, что СМО находится в состоянии 
, когда один канал занят:
.
2) Вероятность того, что СМО находится в состоянии 
, т. е. когда два канала заняты:
3) Вероятность того, что СМО находится в состоянии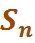 
т. е. когда все каналы заняты:
= 
Теперь для n -канальной СМО с отказами
Относительная пропускная способность:
Q = 1- 
- средняя доля заявок, обслуживаемых системой. При этом А = λQ, где Q = 1 -
Вероятность отказа: = - вероятность того, что заявка покинет СМО необслуженной. Очевидно, что = 1 - Q.
Среднее число занятых каналов (среднее число заявок, обслуживаемых одновременно):
При этом
Пример. Имеется технологическая система (участок), состоящая из трех одинаковых станков. В систему поступают для обработки детали в среднем через 0,5 часа. Среднее время () изготовления одной детали равно 0,6 ч. Если при поступлении заявки на изготовление детали все станки заняты, то деталь направляется на другой участок таких же станков. Найти финальные вероятности состояний системы и характеристики (показатели эффективности) данной СМО.
Решение. λ = 
= 
= 2, т. е. в среднем две заявки на обработку деталей в час.
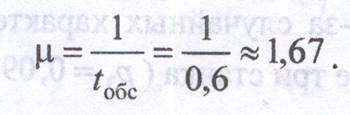
Граф состояний системы представлен на рис. 2.
Возможные состояния системы:
- в СМО (на участке) нет ни одной заявки;
- в СМО (на участке) одна заявка;
- в СМО (на участке) две заявки;
- в СМО (на участке) три заявки (заняты все три станка).
Вероятность того, что все станки свободны:
Вероятность того, что один станок занят:
Вероятность того, что два станка заняты:
Вероятность того, что все три станка заняты:
То есть в среднем в этой системе обрабатывается 1,82 дет/ч (примерно 91 % направляемых деталей), при этом примерно 9 % деталей направляются для обработки на другие участки. Одновременно в среднем работает в основном один станок (= 1,09). Но из-за случайных характеристик потока заявок иногда работают одновременно все три станка (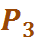 
= 0,09), отсюда 9 % отказов.
|
|
|
|
|
|
