 |
СМО с ожиданием и ограниченной длиной очереди
|
|
|
|
Заявка, поступившая в систему с ожиданием с ограниченной длиной очереди и нашедшая все каналы и ограниченную очередь занятыми, покидает систему необслуженной.
Основной характеристикой качества системы является отказ заявке в обслуживании.
Ограничения на длину очереди могут быть:
1. из-за ограничения сверху времени пребывания заявки в очереди;
2. ограничения сверху длины очереди;
3. ограничения общего времени пребывания заявки в системе.
По ниже написанным формулам можно рассчитать СМО с ожиданием и с ограниченной длиной очереди:
1. Вероятность простоя каналов обслуживания, когда нет заявок (k = О):
2. Вероятность отказа в обслуживании:
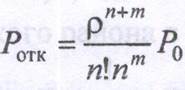
3. Вероятность обслуживания:
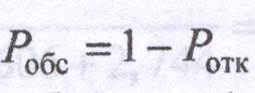
4. Абсолютная пропускная способность:
А = * λ.
5.Среднее число занятых каналов: 
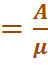
6.Среднее число заявок в очереди:
7.Среднее время ожидания обслуживания:
8.Среднее число заявок в системе:
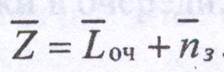
9.Среднее время пребывания в системе:
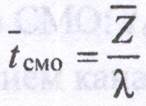
Пример 1. На АЗС установлена 21 колонка для выдачи бензина. Около станции находится площадка на три автомашины для ожидания заправки. На станцию прибывает в среднем 25 машин в час, среднее время заправки одной автомашины - 2,5 мин. Определить вероятность отказа.
Решение. n = 2, m = 3, λ = 0,42 машин/мин, μ = 0,4 машин/мин, ρ = 1,05.
1. Вероятность простоя колонок АЗС:
2. Вероятность отказа в обслуживании
3. Вероятность обслуживания
4. Абсолютная пропускная способность:
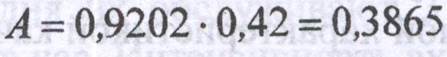
5. Среднее число занятых обслуживанием каналов:
6.Среднее число заявок в очереди:
7. Среднее время ожидания обслуживания:
8. Среднее число заявок в системе:
9. Среднее время пребывания на стоянке:
Вероятность отказа в обслуживании составляет
|
|
|
0,8 %.
Пример 2. Магазин получает ранние овощи из пригородных теплиц. Автомобили с грузом прибывают в разное время с интенсивностью λ=6 машин в день. Подсобные помещения и оборудование для подготовки
овощей к продаже позволяют обрабатывать и хранить товар, привезенный двумя автомашинами (m = 2). В магазине работают три фасовщика (n = 3), каждый из которых в среднем может обрабатывать товар с одной машины в течение = 4 ч. Продолжительность рабочего дня при сменной работе составляет 12 ч.
Определить, какова должна быть емкость подсобных помещений, чтобы вероятность полной обработки товаров была ≥ 0,97.
Решение. Определим интенсивность загрузки фасовщиков:
1. Найдем вероятность простоя фасовщиков при отсутствии машин (заявок):
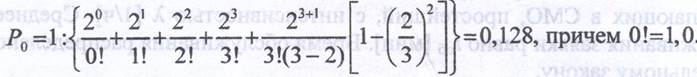
2. Вероятность отказа в обслуживании:
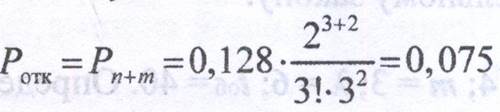
3.Вероятность обслуживания:
Так как = 0, 925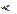 
=0, 97, произведем аналогичные вычисления для m = 3, получим 
=0,122, =0,048, =0,952.
Так как = 0,965 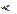=0, 97, примем
m = 4.
Для этого случая =0,12, =0,028, = =0,972, 0,972 
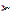0,97, емкость подсобных помещений необходимо увеличить до m = 4.
Для достижения заданной вероятности обслуживания можно увеличивать число фасовщиков, проводя последовательно вычисления СМО для n = 4,5 и т. д. Задачу можно решить, увеличивая емкость подсобных помещений, число фасовщиков, уменьшая время обработки товаров.
Найдем остальные параметры СМО для рассчитанного случая при =0,12, =0,028, = =0,972.
4. Абсолютная пропускная способность: А=0,972*6=5,832 авт./дн.
5. Среднее число занятых обслуживанием каналов (фасовщиков):
= 
=1,944.
6. Среднее число заявок в очереди:
7. Среднее время ожидания обслуживания:
дн.
8. Среднее число машин в магазине :
авт.
9. Среднее время пребывания машины в магазине:
= 
Таким образом, емкость подсобных помещений магазина должна вмещать товар, привезенный четырьмя автомашинами (m = 4), при этом вероятность полной обработки товара будет = 0, 972.
|
|
|
|
|
|
