 |
Линейные преобразования (операторы). Матрица линейного преобразования
|
|
|
|
Линейное векторное пространство. Линейная зависимость и независимость векторов. Базис и размерность
Линейное векторное пространство. Вектор. Линейные операции с векторами
Определение 1.3.1
Множество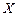 
называется линейным (векторным) пространством, если выполняются следующие два условия:
1) Любым элементам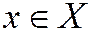 
и 
соответствует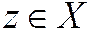 
, который обозначается 
и называется суммой 
и 
.
2) Любому элементу 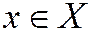и любому числу 
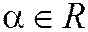ставится в соответствие элемент 
этого множества, который обозначается 
и называется произведением на число 
.
Операции сложения и умножения на число должны быть подчинены аксиомам:
1) 
;
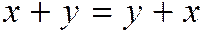2) 
;
3) 
;
4) существует нулевой элемент 
, такой, что 
для любого ;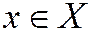
Наиболее важным примером линейного пространства является конечномерное линейное пространство 
с элементами (векторами) вида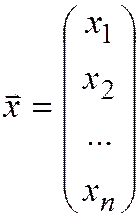 
.
Координатами вектора 
называются значения 
.
Линейная зависимость и линейная независимость векторов
Определение 1.3.2
Пусть даны векторы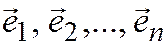 
линейного пространства и числа 
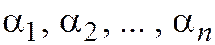. Вектор
называется линейной комбинацией данных векторов.
Определение 1.3.3
Если
только в случае
,
то векторы называются линейно независимыми. В противном случае они линейно зависимы.
Задача 1.3.1
Являются ли векторы 
и 
линейно независимыми?
Решение
Поскольку 
, и, следовательно, 
, то векторы линейно зависимы.
Размерность и базис линейного пространства
Определение 1.3.4
Базисом в линейном пространстве называется набор векторов 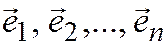, такой, что любой вектор 
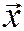этого пространства единственным способом представить в виде:
.
Последняя формула называется разложением вектора 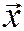по базису 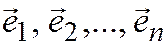, а числа 
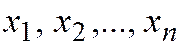координатами 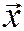в этом базисе.
|
|
|
Определение 1.3.5
Максимальное число линейно независимых векторов линейного пространства называется его размерностью.
Теорема 1.3.1
Конечномерное пространство имеет размерность, равную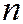 
.
Доказательство
В пространстве можно указать базис из 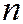линейно независимых векторов:
, 
,…, 
.
С другой стороны векторы 
линейно зависимы, поскольку для:
,
система
Преобразование координат вектора при переходе к другому базису
Координаты любого вектора 
– это координаты его в некотором заданном базисе 
, т.е.
.
Если требуется найти координаты вектора в другом базисе 
, и если заданы координаты нового базиса в старом базисе :
, 
,…, 
,
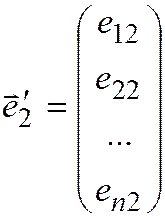то следует составить матрицу перехода:
,
поставив координаты векторов нового базиса в ее столбцы.
Тогда вектор 
с координатами 
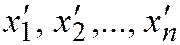в новом базисе определяется из матричного уравнения
,
решение которого при невырожденной матрице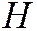 
имеет вид:
.
Задача 1.3.2
Разложить вектор 
пространства 
по базису векторов: 
, 
и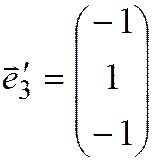 
.
Решение
Матрица перехода имеет вид:
.
Обратная матрица:
.
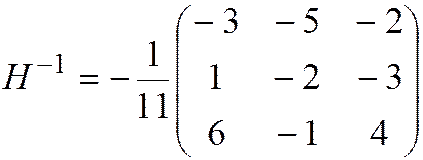Тогда вектор в новом базисе имеет вид:
.
Это значит, что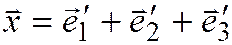 
.
Если матрицей перехода является единичная матрица 
, то
.
Это означает, что координаты вектора 
не меняются при переходе к базису
, 
,…, 
.
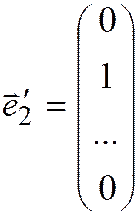Этот базис называют каноническим.
Линейные преобразования (операторы)
Линейные преобразования (операторы). Матрица линейного преобразования
Определение 1.4.1
Линейным преобразованием (линейным оператором) в линейном пространстве называется отображение 
этого пространства на себя, обладающее двумя свойствами:
1) 
;
2) 
;
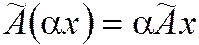где 
и 
– образы элементов (векторов) и , а – вещественное число.
Если линейный оператор 
и если 
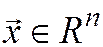, а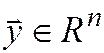 
– образ 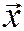и при заданном отображении, то это обозначают:
.
Если при этом в линейном пространстве задан базис , то соответствие между векторам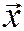и и 
можно записать в виде матричного уравнения:
|
|
|
,
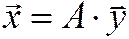где векторы 
и 
заданы в базисе , а матрица 
называется матрицей преобразования (оператора) .
Например, матрицей оператора подобия:
является матрица
,
поскольку
.
Матрица A линейного преобразования 
в базисе связана с матрицей 
этого же преобразования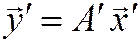 
в новом базисе формулой:
,
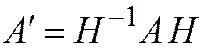где H – матрица перехода.
Задача 1.4.1
Как изменится матрица 
линейного преобразования при переходе к базису 
, 
, 
?
Решение
Матрица перехода к базису 
:
,
обратная матрица:
.
Тогда
|
|
|
12 |
