 |
Собственные числа и собственные векторы матрицы
|
|
|
|
Определение 1.4.2
Пусть квадратная матрица 
– матрица линейного оператора 
в линейном пространстве 
. Ненулевой вектор 
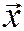называется собственным векторомматрицы 
и оператора , если выполняется:
, (1.4.1)
где 
– называется собственным числом матрицы и оператора.
Векторное равенство (1.4.1) можно записать в виде:
, (1.4.2)
где 
– единичная матрица той же размерности, что и матрица .
Следовательно, собственный вектор 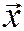является ненулевым решением однородной системы (1.4.2), а собственные числа определяются из условия:
. (1.4.3)
где
.
Задача 1.4.2
Найти собственные числа и собственные векторы матрицы 
.
Решение
Для собственных чисел справедливо равенство:
.
Прибавим ко второму столбцу первый, умноженный на 2. Получим:
.
Из второго столбца можно вынести множитель 
:
.
Прибавим к первой строке вторую, умноженную на 
, и используем теорему разложения:
,
,
,
, 
.
Следовательно, 
.
Собственные числа: 
, 
.
Найдем собственные векторы, соответствующие найденным собственным числам.
1. 
. Матрица однородной системы 
.
Решение однородной системы:
Для координат первого собственного вектора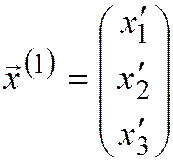 
справедливо уравнение: 
или 
Если 
– свободные неизвестные, то первый собственный вектор:
,
где 
и 
– фундаментальная система решений, 
– любые вещественные числа, не равные нулю одновременно.
2. 
. Матрица однородной системы 
. Решение однородной системы:
Отсюда 
. Обозначая свободное неизвестное 
, найдем второй собственный вектор:
.
Евклидово пространство
Определение 1.4.3
Линейное пространство называется евклидовым, если любым двум его элементам 
и 
ставится в соответствие вещественное число, которое обозначается 
и называется скалярным произведением и которое подчинено следующим аксиомам:
|
|
|
1) 
;
2) 
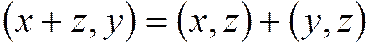, где 
– элемент линейного пространства;
3) 
, где 
– вещественное число;
4) 
, 
, если – нулевой элемент.
Примером евклидова пространства является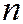 
– мерное векторное пространство , в котором скалярное произведение двух векторов 
и 
определяется соотношением:
.
Ясно, введенное скалярное произведение удовлетворяет всем четырем аксиомам.
Для скалярного произведения элементов и любого евклидова пространства выполняется неравенство:
,
которое называется неравенством Коши–Буняковского.
Определение 1.4.4
Нормой элемента в линейном пространстве называется вещественное число 
, которое ставится в соответствие этому элементу и которое подчинено следующим аксиомам:
1) 
, 
, если – нулевой элемент;
2) 
, где – вещественное число;
3) 
(неравенство Минковского), где элемент линейного пространства.
Если линейное пространство является евклидовом, то определенная равенством
(1.4.4)
норма удовлетворяет всем требуемым аксиомам.
В 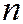– мерном векторном пространстве норма вектора определяется соотношением:
. (1.4.5)
Задача 1.4.3
Скалярное произведение векторов 
и 
пространства 
равно:
.
Скалярное произведение векторов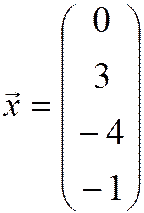 
и 
пространства 
равно:
.
Задача 1.4.4
Норма вектора 
пространства равна:
.
Норма вектора 
пространства равна:
.
Определение 1.4.5
Два элемента евклидова пространства и называются ортогональными, если их скалярное произведение равно нулю.
Например, векторы 
и 
ортогональны, так как 
.
Определение 1.4.6
Если норма элемента (вектора) евклидова пространства 
, то называется нормированным.
Определение 1.4.7
Базис векторов 
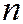– мерного векторного евклидова пространства называется ортонормированным, если:
.
Примером ортонормированного базиса является базис (канонический) векторов
|
|
|
, 
,…, 
.
|
|
|
12 |
