 |
Повторные испытания. Схема Бернулли.
|
|
|
|
Эксперимент. Случайный эксперимент.
С.Э. – эксперимент, исход которого нельзя заранее предсказать
Случайное событие.
С.С. – 
факт, который может произойти/не произойти при проведении С.Э. при данном комплексе условий.
Частота случайного события. Устойчивость частот.
Ч.С.С. – отношение количества наступлений интересующего нас события А в испытаниях, к количеству испытаний. У.Ч. – колебание значения Ч.С.С. около некоторого, среднего значения (опыт с монетой).
Статистическое определение вероятности случайного события.
Вероят-ю событ. А наз-ся предел к которому стремится частота событ. А при неогран. увелич. числа опытов 
Достоверное событие. Невозможное событие.
Событ. которое при наступл. данного комплекса услов. всегда наступает, наз-ся Д.С.(
), а которое наступить не может Н.С.(
)
Элементарное событие. Пространство элементарных событий.
Э.С. это такое событие 
, которое принадлежит пространству элемент. событ., т.е. принадл. множ-ву достоверных событий 
Сумма случайных событий.
Сумма с.с. – событие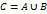 
наступающее 
когда наступает А или B или оба вместе
Произведение случайных событий.
Произвед. с.с. – событие 
наступающее когда А и B наступают одновременно
Разность случайных событий.
Разн. с.с. – событие 
наступающее 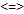когда событие А наступает, а B нет.
Противоположное событие.
Событ.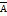 
противоположно событ. А, если оно наступает 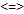когда событие А не наступает
Несовместное событие. А влечет В.
События несовместны, если они не могут произойти одновременно 
. Событ. А влечет за собой соб. B если каждый раз когда наступает А, наступает и B т.е. 
Сигма-алгебра событий.
-алгеброй событ. F наз-ся непустая сист. подмножеств из удвл. св-вам: 1. Если 
; 2. Если 
то и их объедин. и пересеч. принадл. F: 
, 
|
|
|
Классическое определение вероятности.
Вер-ю соб. А наз-ся отношения числа 
благоприятствующих соб. А элем. исходов (т.е. входящих в А) к общему числу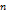 
равновозможн. элем. исходов
Правила комбинаторики. Формулы комбинаторики.
Размещения из n элементов по k: 
. Перестановки из n элементов: 
. Сочетания из n элементов по k (порядок следования элементов не важен): 
. Перестановки с повторениями: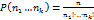 
. Сочетания с повторениями из элементов n различных типов по k элементов: 
. Размещения с повторениями (комбин. из элементов n типов по k элементов, комбин. различ. порядком следования элементов, числом повторений элементов, например ввод пароля):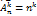 
Геометрическое определение вероятности.
Вер-ю соб. А наз-ся отношение меры множ. А к мере множ. : 
Условная вероятность.
Усл. вер. соб. А при условии наступления события B наз-ют отношение вер. пересеч. соб. 
к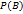 
, при условии, что B наступило. 
, 
Формулы умножения вероятностей.
Теорема: Если 
, 
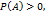то 
Независимость событий. Зависимость событий.
Соб. А и В имеющие ненулевую вероятность наз-ся независимыми если условн. вер. 
совпадает с безусловной вер., т.е.
или 
, иначе А и В – зависимые соб. Соб А и В независ <=> 
Независимость в совокупности.
Соб. 
наз-ся независ. в совокупн. если вер. произвед. 
событ. равна произвед. вер. этих событий (
)
Попарная независимость событий.
Соб. наз-ся независ. в совокупн. если вер. произвед. двух из них равна произвед. вер. этих двух событий
Гипотезы. Полные группы событий.
Априорная вероятность. Апостериорная вероятность.
– попарно не совместные события, одно из них обязательно наступит (т.е. гипотезы). P(H) – априорная вероятность, P(Н/А) – апостериорная.
Повторные испытания. Схема Бернулли.
П.И. – послед-ное. провед. n раз одного и того же опыта или одновременное проведение n одинаковых опытов. С.Б. – послед-ть независ. испытаний (вер. успеха/неуспеха не зависит от предыдущих опытов, и всегда неизменна) итогом которых явл. успех А или неуспех
|
|
|
|
|
|
