 |
Интеграл Лапласа. Его свойства.
|
|
|
|
И.Л. – фун.  .Если k – кол-во успехов, n – число испыт., р – вер. успеха, q –вер. неуспеха,
.Если k – кол-во успехов, n – число испыт., р – вер. успеха, q –вер. неуспеха, 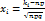 , i=1,2, то
, i=1,2, то  .
.
Случайная величина.
С.В – числовая величина, знач которой зависит от того, какой именно элем. исход произошел в рез-те опыта. Числ. фун.  заданную на простр. эл. исходов наз-ют с.в. если
заданную на простр. эл. исходов наз-ют с.в. если  множ.
множ.  явл. случ. соб.
явл. случ. соб.
Закон распределения вероятностей случайной величины.
Правило (как правило это функция распределения), позволяющее находить вер. того, что с.в. примет значение из подмножества её значений.
Функция распределения.
Ф.Р. – фун 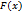 знач. которой в т. x равно вер. соб. {X<x}, т.е. соб. сост. только из тех эл. исх. ω для которых X(ω)<x
знач. которой в т. x равно вер. соб. {X<x}, т.е. соб. сост. только из тех эл. исх. ω для которых X(ω)<x
Дискретная величина. Ряд распределения.
С.в. Х наз-ся дискр. если множ. ее знач. конечно или счетно. Р.Р. – табл, 1стр – знач. с.в. 2стр – вер. 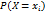
Непрерывная случайная величина. Плотность.
Н.с.в. – с.в. X., фун. распред. которой можно представить виде 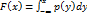 где
где  – плотность распред. с.в.
– плотность распред. с.в.
Математическое ожидание дискретной случайной величины.
М.о.д.с.в. – сумма произвед. значений 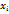 с.в. и ее вероятностей
с.в. и ее вероятностей 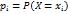
Математическое ожидание непрерывной случайной величины.
М.о.н.с.в. – сходящийся абс. несобств. интеграл 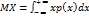
Свойства математического ожидания.
M*const=const; M(aX+b)=aMX+b; M(aX)=aMX; M(X1+X2)=MX1+MX2; если X1,X2-независ. с.в.: M(X1*X2)=MX1*MX2
Дисперсия СВ. Дисперсия дискретной СВ. Дисперсия непрерывной СВ.
Д.с.в. – это мат. ожид. квадрата отклонения с.в. Х от ее мат. ожид.  .
.
Для дискр:  . Для непрер.
. Для непрер. 
Начальный момент к – порядка.
Это 
Центральный момент к – порядка.
Это 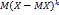
Свойства дисперсии.
Если с.в. Х принимает только одно знач. const с вер. 1 то DC=0; 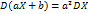 ; Если X1,X2 – независ. D(X1+X2)=DX1+DX2
; Если X1,X2 – независ. D(X1+X2)=DX1+DX2
N-мерный случайный вектор.
N-м.с.в.  – совокупн. с.в.
– совокупн. с.в. 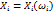 заданных на одном вероятностном простр. (
заданных на одном вероятностном простр. ( )
)
|
|
|
Функция распределения n – мерного случайного вектора. Вероятностный смысл.
Фун., знач. которой в т. 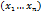 равно вер. совместн. наступл. событ.
равно вер. совместн. наступл. событ.  , т.е. P(
, т.е. P( )
)
Вер. смсл двумерн с.в. –  - вер попад. случ. вектора
- вер попад. случ. вектора  в квадрант с вершинами
в квадрант с вершинами 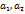
Двумерная дискретная величина.
Двум.с.в.  наз-ся дискр если каждая из с.в.
наз-ся дискр если каждая из с.в.  явл. дискр.
явл. дискр.
Непрерывная двумерная СВ. Двумерная плотность.
Непр.двум.с.в. 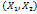 это такая двум.с.в.
это такая двум.с.в. 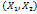 , совмест-ю фун. распред. которой
, совмест-ю фун. распред. которой  (
( ) можно представить в виде сход. несобств. интеграла
) можно представить в виде сход. несобств. интеграла  где
где  – совмест-я двум. плотн. распред. с.в.
– совмест-я двум. плотн. распред. с.в. 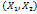
Независимость СВ.
С.в. 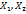 наз-ся независ-ми. если совместн. фун. распред.
наз-ся независ-ми. если совместн. фун. распред.  явл произвед. одномерных фун. распред.
явл произвед. одномерных фун. распред.

Определение ковариации. Формула вычисления дискретной СВ; непрерывной СВ.
Ков. с.в. 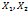 наз-ся мат. ожид. произв. отклон-ий. с.в. от их мат. ожид.
наз-ся мат. ожид. произв. отклон-ий. с.в. от их мат. ожид.
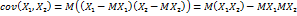 .
.
Для дискр: 
Для непрер: 
Некоррелированность CВ.
Если 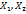 - независимы, то они некоррелируемы, т.е.
- независимы, то они некоррелируемы, т.е. 
Матрица ковариации.

Коэффициент корреляции.
К.к. это 
Симметричность СВ относительно математического ожидания.
С.в. наз-ся симметрично распред. относительно мат. ожид. если  . В случ непрер.с.в.Х симметр-ть. <=> когда график плотности симметричен относительно прямой
. В случ непрер.с.в.Х симметр-ть. <=> когда график плотности симметричен относительно прямой  .
.
Асимметрия.
 . Для симметрично распред. относительно мат. ожид. с.в. Х асимметрия равна 0. Если A>0 то кривая распределения (плотность) более полога справа от моды с.в., и наоборот если A<0
. Для симметрично распред. относительно мат. ожид. с.в. Х асимметрия равна 0. Если A>0 то кривая распределения (плотность) более полога справа от моды с.в., и наоборот если A<0
Эксцесс.
 . Эксцесс характеризует островершинность или плосковершинность распределения. Для нормального распред.
. Эксцесс характеризует островершинность или плосковершинность распределения. Для нормального распред. 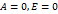 . Остальные распределения сравниваются с нормальным: если Е>0 – более островершинные и наоборот для Е<0.
. Остальные распределения сравниваются с нормальным: если Е>0 – более островершинные и наоборот для Е<0.
Мода.
Модой  наз-ся значение с.в. Х, принимаемое с наибольшей вероятностью по сравн. с двумя соседними знач. В случ. непрер. с.в. Х, мода – точка (локального) максимума плотн. Если мода единственна, то распределение наз-ся унимодальным, иначе – полимодальным.
наз-ся значение с.в. Х, принимаемое с наибольшей вероятностью по сравн. с двумя соседними знач. В случ. непрер. с.в. Х, мода – точка (локального) максимума плотн. Если мода единственна, то распределение наз-ся унимодальным, иначе – полимодальным.
|
|
|
Медиана.
Медианой  с.в. Х наз-ся такое ее знач.
с.в. Х наз-ся такое ее знач.  для которого
для которого 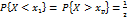 . Используя фун. распред. это равенство можно переписать так же как
. Используя фун. распред. это равенство можно переписать так же как 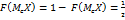
Квантиль.
К. уровня  с.в. Х наз-ся число
с.в. Х наз-ся число  удвл. нерав.:
удвл. нерав.: 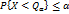 и
и  где
где  .
.  -квантиль наз-ся медианой с.в. Х
-квантиль наз-ся медианой с.в. Х
Сходимость почти наверное
Последоват. с.в.  сход к нулю с вероятностью 1 (почти наверное) если
сход к нулю с вероятностью 1 (почти наверное) если 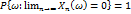 , т.е.
, т.е.  . Из сход. почти наверное следует сход. по. вероятн.
. Из сход. почти наверное следует сход. по. вероятн.
Сходимость по вероятности
Если последоват. с.в.  удвл. условию
удвл. условию  , то говорят о сход-ти этой послед. к нулю по вероятн.
, то говорят о сход-ти этой послед. к нулю по вероятн. 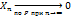 . Из сход. по вер. следует слабая сход.
. Из сход. по вер. следует слабая сход.
|
|
|


