Решение задачи оптимального использования ресурса с помощью надстройки “Поиск решения” в среде MS Excel

ЛАБОРАТОРНАЯ РАБОТА № 2

По дисциплине «Имитационное моделирование»

Модели оптимального распределения ресурса

Цель занятия:

- ознакомиться с математическими моделями оптимального распределения ресурсов;

- освоить методы построения моделей линейного программирования;

- освоить методы решения задач оптимального распределения ресурсов с помощью программы MS Excel.

Немного теории

Довольно часто в управлении возникают задачи оптимального рас­пределения ресурсов, планирования производства, организации рабо­ты транспорта и т.д. В таких практических задачах "расходы" и "дохо­ды" линейно зависят от количества закупленных или средств (например, суммарная стоимость партии товаров линейно за­висит от количества единиц товара; оплата перевозок линейно зависит от веса перевозимого груза и т.д.).

Задачи, решаемые с помощью специальных методов нахождения оптимального решения в зонах "линейных ограничений", получили название задач линейного программирования. Полное название та­ких задач не совсем удачно, так как слово "программирование" пре­дусматривает только машинное средство достижения оптимумов (ча­сто из-за большой трудоемкости вычислений), но не смысл самого метода.

Чтобы стала понятной идея линейной оптимизации, рассмотрим пример постановки задачи и формирования математической модели. Для изготовления двух видов продукции П₁ и П₂ используются три вида сырья: с₁ с₂ и с₃. Запасы сырья на складе в количестве единиц сырья, затрачиваемых на изготовление единицы продукции, приведе­ны в табл. 1.

Таблица 1 - Затраты и запасы сырья

Вид сырья	Запас сырья	Количество единиц сырья на изготовление единицы продукции
П1	П2
C 1 C2 C3   сз

 

Прибыль от реализации единицы продукции П₁ составляет 50 руб., а продукции П₂ — 40 руб.

Необходимо составить такой план выпуска продукции, чтобы при ее реализации получить максимальную прибыль.

Обозначим через x₁ количество единиц продукции П₁, а через х₂ — количество единиц продукции П₂. Тогда, учитывая количество единиц сырья, расходуемое на изготовление единицы продукции, а также запасы сырья, получим систему ограничений:

,

которая показывает, что количество сырья, расходуемое на изготовление продукции, не может превысить имеющихся запасов.

Конечную цель решаемой задачи — получение максимальной при­были от реализации продукции — выразим как функцию двух пере­менных x₁ и x₂. Реализация x₁ единиц продукции П₁ дает прибыль 50х₁, реализация x₂ единиц продукции П₂ дает 40х₂ рублей прибыли. Сум­марная прибыль будет

Необходимо найти такие неотрицательные значения x₁ и x₂, при кото­рых функция L достигает максимума. Условиями не оговорена неделимость единицы проекции, поэтому x₁ и x₂ могут быть и дробными числами.

 

Решение задачи оптимального использования ресурса с помощью надстройки “Поиск решения” в среде MS Excel

 

Ознакомимся с методами решения задач линейного программирования с помощью MS Excel. Пусть дана общая задача линейного программирования в виде:

 

- целевая функция,

- неравенства ограничения,

- условие не отрицательности.

1. Для решения задачи внесем необходимые надписи в ячейки 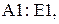А2:А4. Отметим, что содержание этих надписей не оказывает никакого влияния на решение задачи.

2. Зададим адреса ячеек, в которых будет помещен результат решения (изменяемые ячейки). Оптимальные значения . Оптимальное значение целевой функции - .

3. Введем исходные данные задачи (рис. 1):

 

	А	В	С	D	E
	Переменные			Значения целевой функции	Ограничения
	Значения
	Коэффициент целевой функции
	Коэффициент ограничений		3,5
			0,5

 

Рис. 1 – Исходные данные

 

- в ячейки 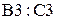значения коэффициентов целевой функции:

- в ячейки 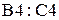введем значения ограничений, взятых из системы неравенств-ограничений;

- в ячейки 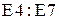введем значения правых частей ограничений

4. Ввести зависимость для целевой функции. Это можно сделать, введя в ячейку D2 формулу: =СУММПРОИЗВ(В2:С2;В3:С3). А можно использовать панель инструментов. Для этого поместим курсор в ячейку D2. Затем поместим курсор на кнопку «Мастер функций» на панели инструментов - появляется диалоговое окно «Мастер функций»; в окне «Категория» выбрать «Математические», а в окне «Функций» - СУММПРОИЗВ.

В строку «Массив 1» ввести В2:С2;

В строку «Массив 2 «ввести В3:С3.

Массив 1 будет использоваться при вводе зависимостей для ограничений, поэтому на этот массив надо сделать абсолютную ссылку, т.е. представить в виде $B$2: $С$2. Окончательно в ячейке D2 будет запись

= СУММПРОИЗВ ($B$2: $С$2; В3: С3).

5. Ввести зависимости для ограничений.

Поместим курсор в ячейку D4 и введем формулу: = СУММПРОИЗВ ($B$2:$С$2; В4:С4).

Скопируем формулу, введенную в ячейку D4 в ячейки D5, D6, D7. Так, чтобы скопировать в D5 необходимо:

- поместить курсор в ячейку D4;

- на панели инструментов нажать кнопку «Копировать в буфер».

- на панели инструментов нажать кнопку «Вставить из буфера».

В ячейке D5 будет запись = СУММПРОИЗВ ($B$2: $С$2; В5: С5).

Аналогично проделать для ячеек D6 и D7.

6. Ввести команду «Поиск решения», для чего выполнить операции главного меню: «Сервис» ® «Поиск решения».

- после появления диалогового окна «Поиск решения» выполнить следующие действия:

- в поле с именем «Установить целевую ячейку» ввести абсолютный адрес: $D$2.

- для группы «Равной» выбрать вариант поиска решений «Максимальному значению».

- в поле с именем «Изменения ячеек» ввести абсолютный адрес ячеек $B$2: $С$2.

Добавить четыре ограничения. Для задания первого ограничения нажать кнопку с надписью «Добавить»:

- в появившемся дополнительном окне выбрать ячейку $D$4, которая должна отобразиться в поле «Ссылка на ячейку»;

- в качестве знака ограничения выбрать нестрогое неравенство «< =»;

- в качестве правой части ограничения выбрать ячейку $E$4;

- для действия первого ограничения в диалоговом окне «Поиск решения» нажать кнопку «Добавить.

Аналогично вводятся оставшиеся три ограничения. Окончательно в окне «Ограничения» будет следующая запись:

$D$4 < = $E$4

$D$5 < = $E$5

$D$6 < = $E$6

$D$7 > = $E$7

Нажать кнопку «Параметры». В дополнительном окне параметры поиска выбрать отметки «Линейная модель» и «Неотрицательные значения». Далее нажать «ОК» и в окне «Поиск решения» кнопку «Выполнить».

После выполнения расчетов будет получено количественное решение, которое имеет вид (рис.2):

 

	А	В	С	D	E
	Переменные			Значения целевой функции	Ограничения
	Значения
	Коэффициенты целевой функции
	Коэффициент ограничений		3,5
			0,5

 

Рис. 2 – Результаты решения.

 

Таким образом, в результате решения задачи получен оптимальный план со значениями , что обеспечивает максимальное значение целевой функции, равной 2300 ед.

 

12	Поделиться:

Воспользуйтесь поиском по сайту: