Критерии оценки помехоустойчивости информационных систем

Под помехоустойчивостью понимают способность информационной системы противостоять вредному действию помех. В результате действия помех принятое сообщение будет в какой-то мере отличаться от переданного. Поэтому помехоустойчивость можно характеризовать как степень соответствия принятого сообщения переданному при заданной помехе. При сравнении нескольких систем та из них будет более помехоустойчивой, которая при одинаковой помехе обеспечит меньшее различие между принятым и переданным сообщениями.

Имеется несколько способов введения количественных характеристик помехоустойчивости. Рассмотрим сначала способы описания помехоустойчивости дискретных систем. Эти системы характерны тем, что все возможные сигналы конечной длительности образуют дискретное конечное множество; пусть общее число возможных сигналов равно N. Действие шумов сводится к тому, что некоторые символы в сигнале подменяются другими, в результате чего вместо переданного (например, i- го) сигнала принимается другой (например, k- й) сигнал. Помехоустойчивость системы связи наиболее полно может быть охарактеризована набором вероятностей { P_ik } того, что при передаче i- го сигнала будет принят k- й (i,k= 1,2,..., N); и если мы хотим задать требования к помехоустойчивости системы с учетом ценности каждого из сообщений в отдельности, то задание всей матрицы { P_ik } необходимо.

Однако сравнение систем по их матрицам { P_ik } (которые можно назвать «стохастическими матрицами трансформации сообщений» связано с рядом затруднений, а часто и не необходимо: достаточно ввести более простые характеристики помехоустойчивости. К таким простым параметрам относится, например, средняя вероятность ошибочного приема, Р _ош.ср.:

(9.2)

где p_i – вероятность передачи i- го сигнала.

Другим собирательным параметром, характеризующим помехоустойчивость системы, может служить остаточная средняя неопределенность относительно переданного сообщения, т.е. энтропия

Н₀ = -(1 – Р _ош.ср.) log (1 – P _ош._ср.) – Р _ош.ср. log Р _ош.ср. (9.3)

Для непрерывных систем связи описание помехоустойчивости требует специфического подхода, так как множество возможных сигналов даже конечной длительности несчетно. Действие шумов в линии связи сводится к тому, что вместо отправленного сигнала x(t) на выходе премника наблюдается другая функция времени, y(t). Чем ближе y(t) к x(t) при заданном шуме, тем более устойчива система по отношению к данной помехе. Для количественного описания помехоустойчивости необходимо ввести меру различия двух функций x(t) и y(t). Чаще всего в качестве такой меры принимается средний квадрат разности сравниваемых функций:

(9.4)

«Расстояние» между функциями x(t) и y(t) может быть также определено с помощью так называемой абсолютной ошибки

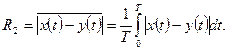(9.5)

Другим способом является «частотно-взвешенный эффективный критерий» [4]. Идея этого критерия состоит в том, чтобы придавать различным частотным компонентам разности х и у разные веса. Это эквивалентно пропусканию разности x(t) – y(t) через фильтр с определенной переходной функцией h(t); выходной сигнал такого фильтра выразится как

(9.6)

«Расстояние» между функциями x(t) и y(t) определится как средняя мощность сигнала на выходе рассматриваемого гипотетического фильтра:

(9.7)

Введенные выше меры различия отправляемого и принимаемого сигналов могут служить основой для характеристики помехоустойчивости систем. Например, система может считаться достаточно помехоустойчивой, если «расстояние» между отправленным сигналом и сигналом на выходе системы не превышает заданной величины.

В качестве меры помехоустойчивости могут быть приняты и другие числовые характеристики, например, логарифм обратной величины среднеквадратичной ошибки в непрерывном случае, минус логарифм вероятности ошибки в дискретном случае, различным способом введенные понятия эквивалентного отношения сигнала к шуму и пр.