Способы повышения помехоустойчивости информационных систем

В настоящее время известно большое число способов повышения помехоустойчивости систем.

Простым и часто применяемым способом повышения помехоустойчивости передачи является увеличение отношения сигнал/помеха за счет увеличения мощности передатчика. Однако этот метод, несмотря на свою простоту может оказаться экономически невыгодным, так как связан с существенным ростом сложности и стоймости оборудования. Помимо того, увеличение мощности передачи сопровождается усилением мешающего действия данного канала на другие.

Важным способом повышения помехоустойчивости передачи непрерывных сигналов является рациональный выбор вида модуляции сигналов. Применяя виды модуляции, обеспечивающие значительное расширение полосы частот сигнала, можно добиться существенного повышения помехоустойчивости передачи.

Радикальным способом повышения помехоустойчивости передачи дискретных сигналов является использование специальных помехоустойчивых кодов. Такие коды позволяют обнаруживать и устранять искажения в кодовых комбинациях за счет введения в код дополнительных, избыточных символов. Кодирование сопровождается увеличением времени передачи или частоты передачи символов кода. Это приводит к расширению спектра сигнала.

Ниже рассматриваются основные положения теории помехоустойчивого кодирования.

Разновидности помехоустойчивых кодов. Высокие требования к достовер­ности передачи, обработки и хранения информации в современных телекоммуникационных системах диктуют необходимость такого кодирования информации, которое обеспечивало бы воз­можность обнаружения и исправления ошибки.

Кодирование должно осуществляться так, чтобы сигнал, соответствующий принятой последо­вательности символов, после воздействия на него пред­полагаемой в канале помехи оставался ближе к сигналу, соответствующему конкретной переданной последователь­ности символов, чем к сигналам, соответствующим дру­гим возможным последовательностям. (Степень близости обычно определяется по числу разрядов, в которых последовательности отличаются друг от друга.)

Это достигается ценой введения при кодировании избыточности, которая позволяет так выбрать передавае­мые последовательности символов, чтобы они удовлет­воряли дополнительным условиям, проверка которых на приемной стороне дает возможность обнаружить и испра­вить ошибки.

Коды, обладающие таким свойством, называют поме­хоустойчивыми. Они используются как для исправления ошибок (корректирующие коды), так и для их обнаруже­ния.

У подавляющего большинства существующих в нас­тоящее время помехоустойчивых кодов указанные усло­вия являются следствием их алгебраической структуры. В связи с этим их называют алгебраическими кодами. (В отличие, например, от кодов Вагнера, корректирующее действие которых базируется на оценке вероятности искажения каждого символа.)

Алгебраические коды можно подразделить на два больших класса: блоковые и непрерывные.

В случае блоковых кодов процедура кодирования заключается в сопоставлении каждой букве сообщения (или последовательности из k символов, соответствую­щей этой букве) блока из п символов. В операциях по преобразованию принимают участие только указан­ные k символов, и выходная последовательность не за­висит от других символов в передаваемом сообщении.

Блоковый код называют равномерным, если п остается постоянным для всех букв сообщения.

Различают разделимые и неразделимые блоковые коды. При кодировании разделимыми кодами выходные последовательности состоят из символов, роль которых может быть отчетливо разграничена. Это инфор­мационные символы, совпадающие с символами после­довательности, поступающей на вход кодера канала, и избыточные (проверочные) символы, вводимые в исход­ную последовательность кодером канала и служащие для обнаружения и исправления ошибок.

При кодировании неразделимыми кодами раз­делить символы выходной последовательности на инфор­мационные и проверочные невозможно.

Непрерывными (древовидными) называют такие ко­ды, в которых введение избыточных символов в коди­руемую последовательность информационных символов осуществляется непрерывно, без разделения ее на неза­висимые блоки. Непрерывные коды также могут быть разделимыми и неразделимыми.

Наиболее простыми в отношении технической реали­зации кодами этого класса являются сверточные (рекуррентные) коды.

Принципы помехоустойчивого кодирования блоками конечной длины. Пусть некоторая последовательность элементарных символов, со­держащая п разрядов, представляет кодовое слово. Если в любом из разрядов кодового слова возможное число различных элементар­ных символов составляет т, можно построить код, состоящий из т^п слов. В том случае, когда все возможные кодовые слова используются для передачи сообщений от источника, код называется простым (при­митивным) или кодом без избыточности. Такой код использовать для кодирования в канале с помехами нецелесообразно. Для придания ко­ду корректирующих свойств в него необходимо ввести избыточность, т.е. использовать для передачи сообщений лишь часть М из числа т^п кодовых слов. Количественно избыточность кода по аналогии с вели­чиной избыточности источника сообщений может быть определена как χ = 1 — log M/(n log m); при этом величину 1 — х = log M/(n log m) = R называют относительной скоростью кода. Число т в теории кодиро­вания называют основанием кода. Простейшими и в то же время наи­более широко используемыми на практике являются двоичные коды, у которых т = 2.

Возможность использования в системе связи кодовых блоков, имеющих одинаковую длительность, существенно упрощает технику пе­редачи дискретных сообщений. Множество всех возможных кодовых блоков длины п можно представить векторами линейного пространства размерности т^п, если под операцией сложения понимать поразрядное сложение по модулю т. В частности, при т = 2, когда символами кода являются 0 и 1, в линейном пространстве можно ввести широко исполь­зуемое в теории кодирования понятие — расстояние Хемминга между кодовыми блоками, под которым понимается поразрядная разность (или сумма) по модулю 2 между двумя любыми векторами пространства 2 ^п. Расстояние Хемминга оказывается равным числу разрядов, в которых символы этих кодовых блоков не совпадают.

Расстояние Хемминга между кодовыми блоками позволяет ввести еще один важный параметр в теории кодирования:

Определение. Наименьшее из расстояний Хемминга между лю­быми парами используемых кодовых слов называется кодовым рассто­янием для кода К и обозначается через d(K).

Рассмотрим принципы помехоустойчивого кодирования на основе блочных равномерных кодов, полагая, что в системе связи принятие ре­шения о переданном сообщении осуществляется по результатам распо­знавания каждого кодового слова из переданной последовательности. При использовании кода без избыточности (примитивного кода, для ко­торого d(K) = 1) появление ошибки в любом из принятых слов останет­ся незамеченным, поскольку трансформация символа хотя бы в одном разряде приводит к используемому кодовому слову. Возможность фик­сации ошибки в кодовом слове появляется только в том случае, когда в процессе кодирования вводится определенная избыточность. Как уже отмечалось, в этом случае из возможного N = mⁿ числа кодовых бло­ков для передачи сообщений от источника используются лишь часть М < N кодовых слов. Будем называть используемые для кодирова­ния блоки разрешенными, а остальные (N — М) блоков — запрещен­ными. В отсутствие помех на выходе канала могут появиться только разрешенные блоки. При передаче по каналу с помехами часть кодо­вых символов может быть принята с ошибками, при этом чаще всего принятый кодовый блок оказывается запрещенным, что свидетельству­ет о наличии ошибки при передаче.

Существует ненулевая вероятность того, что комбинация ошибочно принятых символов преобразует переданное слово в другое разрешен­ное и наличие ошибки останется незамеченным. Разумеется, при раз­работке помехоустойчивого кода стремятся к тому, чтобы вероятность такого события оказалась весьма малой. При декодировании с испра­влением ошибок принятые запрещенные кодовые блоки преобразуются декодером в разрешенные по определенным правилам, установленным для данной системы. Эти правила зависят от свойств канала связи и определяются в соответствии с выбранным статистическим критери­ем. В частности, таковым может быть правило исправления ошибочно принятого блока в наиболее вероятный разрешенный. Конечно, мо­жет оказаться, что наиболее вероятный кодовый блок не соответствует переданному слову. Тем не менее, при удачно разработанном коде достаточно большой избыточности может быть обеспечена высокая ве­роятность исправления ошибки.

При декодировании с исправлением ошибок можно воспользоваться определением кода как множества М пар, состоящих из кодовых слов и соответствующих им групп , за­прещенных блоков. Таким образом, все множество N последо­вательностей конечной длины п разбивается на М непересекающихся подмножеств. Если принятый кодовый блок принадлежит подмножеству Bj, принимается решение, что передавалось кодовое слово . Очевид­но, что при декодировании по критерию максимума правильной вероят­ности в подмножество Bj, помимо слова bj, необходимо включить все те запрещенные кодовые блоки, при приеме которых наиболее вероят­ным является разрешенное кодовое слово bj.

Выбор наилучшего правила, по которому осуществляется декоди­рование с исправлением ошибки, зависит от специфических свойств канала передачи. Действительно, границы между подмножествами , при которых обеспечивается максимум правильной вероятности испра­вления искаженного блока, могут существенным образом зависеть от статистических характеристик канала передачи. Рассмотрим процеду­ру выбора правила исправления ошибок на примере симметричного канала без памяти. Допустим, что в результате прохождения по та­кому каналу кодового слова из-за воздействия помех в q разрядах произошла ошибка, в результате чего на выходе канала был принят блок bj. Пусть d(i,j) есть расстояние Хемминга между блоками и bj, так что q = d(i,j). Тогда вероятность перехода на выходе кана­ла слова bi в блок bj

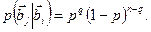(9.12)

Отсюда следует, что в двоичном симметричном канале без памяти при заданных п и т вероятность зависит только от расстояния d(i,j). Отметим, что при вероятности ошибочного приема одного раз­ряда р < 0,5 значение вероятности (9.12) монотонно убывает с увеличе­нием расстояния d(i,j). Следовательно, вероятность приема блока тем меньше, чем больше его расстояние от переданного слова . Если в качестве правила принятия решения о переданном слове при деко­дировании с исправлением ошибки в симметричном канале без памяти выбрать правило декодирования по максимуму вероятности , то в таком канале ошибочный блок следует декодировать как раз­решенное кодовое слово , которое находится на наименьшем рассто­янии от . Декодирование по наименьшему расстоянию (называемое также алгоритмом Хемминга) при равновероятной передаче всех кодо­вых слов является оптимальным для симметричного канала без памяти.

При таком алгоритме декодирования исправляющая способность кода характеризуется следующей теоремой:

Код К при декодировании по наименьшему расстоянию исправляет любые q и менее ошибок в каждом кодовом слове тогда и только тогда, когда кодовое расстояние d(K) ≥ 2q + 1.

Покажем, что действительно переданное слово при d(K) ≥ 2 q +1 по расстоянию оказывается ближе к принятому блоку , чем любое другое кодовое слово. Допустим обратное, т.е. существует кодовое слово , для которого d(k,j) < d(i,j). Тогда в соответствии с те­оремой треугольника справедливо следующее неравенство: d(k, i) £ d(k,j) + d(i,j), или d(k,i) £ 2d(i,j). Однако, по условиям теоремы d(i,j) £ q < d(K)/2 и, следовательно, d(k,i) < d(K), что противоречит определению кодового расстояния.

Обратно, пусть кодовое расстояние d(K) = d £ 2q и , — такие кодовые слова, что d(i, j) = d. Тогда, заменив в q разрядов на соот­ветствующие разряды из , получим вектор , для которого , d(k,j) = d - q £ q. Отсюда следует, что d{i, к) = q, d(k,j) £ q. Сле­довательно, при декодировании слово может быть отождествлено со словом и ошибка не будет исправлена.

Отметим большую значимость кодового расстояния d(K) как ос­новного показателя исправляющих возможностей кода. Поскольку ве­роятность появления каких-либо ошибок кратности q определяется би­номиальным законом

(9.13)

оказываются справедливыми следующие оценки вероятности ошибоч­ного декодирования р_од при исправлении ошибок:

(9.14)

 

Задача помехоустойчивого кодирования состоит в поиске кода, об­ладающего максимально достижимым кодовым расстоянием d(K), или точнее, максимизации кодового расстояния при заданных п — числе символов в кодовом слове и М — числе кодовых слов. Несмотря на то, что для многих значений п и М величина максимально достижимого d[K) получена, в общем виде задача помехоустойчивого кодирования решения не имеет. Реализация процедуры помехоустойчивого коди­рования на первый взгляд не вызывает труда. В память кодера запи­сываются кодовые слова и правило, по которому каждое из состояний источника отождествляется с соответствующим словом, посылаемым в канал. Это правило известно и на декодере. Декодер, приняв блок, искаженный помехой, сравнивает его со всеми М кодовыми словами и отыскивает то из них, которое по Хемминговому расстоянию бли­же остальных к принятому блоку. Можно показать, однако, что даже при умеренных п этот алгоритм декодирования на практике не реализу­ем из-за гигантского объема необходимой памяти и соответствующей системы логической обработки. Поэтому применение достаточно эф­фективных кодов при табличном методе кодирования и декодирования технически невозможно. Это приводит к тому, что одним из основных направлений современной теории кодирования является поиск таких кодов, для которых кодирование и декодирование осуществляются не перебором таблицы, а в результате определенных регулярных правил, основанных на алгебраической теории. К числу таких кодов относятся линейные блочные, в частности, циклические коды.

Наиболее характерной ситуацией использования кодирования является передача дискретных сообщений в реальном времени при ограниченной мощности передатчика. Это означает, что n -символьное кодовое слово должно быть передано за время, равное времени выдачи k символов источником сообщения. Если это ус­ловие не выполняется, то кодирование не имеет смысла, посколь­ку последовательность передаваемых символов сообщения может быть считана с меньшей скоростью и в результате характеристики помехоустойчивости могут быть улучшены за счет увеличения энергии передаваемых символов.

Пусть мощность передатчика равна Р,а длительность сообщения, содержащего k символов, равна T_w. Тогда энергия сигнала, приходящаяся на слово сообще­ния, равна PT_w.

В случае блокового избыточного кодирования имеющаяся энергия распределяется на п символов, поэтому энергия, прихо­дящаяся на кодовый символ, равна PT_w / n. Так как n > k,то при ис­пользовании кодирования энергия, приходящаяся на символ, уменьшается. Это приводит к тому, что в системе с избыточным кодированием вероятность ошибки на символ оказывается выше, чем в системе без кодирования. Если код обладает высокой кор­ректирующей способностью, то благодаря наличию избыточных символов эти потери «отыгрываются» и обеспечивается дополни­тельный выигрыш, который принято называть энергетическим вы­игрышем кодирования (ЭВК). ЭВК является количественной мерой эффективности кодирования. Его значения оценивают, сопостав­ляя энергетические затраты на передачу одного бита при фикси­рованных вероятностях ошибочного приема либо символа, либо бита сообщения в системах с кодированием и без кодирования.

 

Контрольные вопросы

 

1. Какие критерии применяются для оценки помехоустойчивости систем передачи информации с непрерывными сигналами?

2. Какие критерии применяются для оценки помехоустойчивости систем передачи информации с дискретными сигналами?

3. Перечислите известные способы повышения помехоустойчивости передачи.

4. Какие коды называют помехоустойчивыми?

5. За счет чего помехоустойчивый код получает способность обнаруживать и исправлять ошибки?

6. Что подразумевают под кратностью ошибки?

7. Как определяется минимальное кодовое расстояние?

8. Запишите соотношения, связывающие минимальное кодовое расстояние с числом обнаруживаемых и исправляемых ошибок.

9. Назовите основные показатели качества корректирующего кода.

 

⇐ Предыдущая123

Поделиться:

Воспользуйтесь поиском по сайту: