 |
Элементарные преобразования матриц
|
|
|
|
Транспонирование матриц
Определение 1.3. Матрица  , полученная из данной матрицы
, полученная из данной матрицы  заменой каждой ее строки столбцом с тем же номером, называется матрицей, транспонированной относительно данной, т.е. если
заменой каждой ее строки столбцом с тем же номером, называется матрицей, транспонированной относительно данной, т.е. если
 , то
, то  . (1.2)
. (1.2)
Отмети, что если A – матрица размера m ´ n, то матрица AТ имеет размер n ´ m. Операция нахождения матрицы, транспонированной к данной, называется транспонированием матрицы.
Пример 1.2. Пусть дана матрица  . Тогда транспонированная матрица примет вид
. Тогда транспонированная матрица примет вид  .
.
,
Линейные операции над матрицами
Линейными действиями над матрицами называются сложение и вычитание матриц, умножение матрицы на число. Сложение и вычитание матриц определяются только для матриц одинаковых размеров.
Определение 1.4. Суммой двух матриц  и
и  одной размерности называется матрица
одной размерности называется матрица  той же размерности, каждый элемент которой равен сумме соответствующих элементов исходных матриц, т.е.
той же размерности, каждый элемент которой равен сумме соответствующих элементов исходных матриц, т.е.
 . (1.3)
. (1.3)
Под суммой A+B+C трех матриц A, B и С понимается матрица, полученная в результате последовательного сложения этих матриц, т.е. A+B+C =(A+B) +C. Таким же образом можно определить сумму матриц для большего числа слагаемых.
Аналогично определяется разность матриц.
Определение 1.5. Произведением матрицы  на число k называется матрица
на число k называется матрица  той же размерности, в которой каждый элемент матрицы
той же размерности, в которой каждый элемент матрицы  умножен на это число, т.е.
умножен на это число, т.е.
 . (1.4)
. (1.4)
Пример 1.3. Найти матрицу  , где
, где
 ,
,  .
.
Решение.
 ,
,
Определение 1.6. Матрица  называется противоположной матрице A.
называется противоположной матрице A.
Таким образом, разность двух матриц можно определить так:  .
.
Линейные операции над матрицами обладают следующими свойствами, которые примем без доказательства:
1.  ; 5.
; 5.  ;
;
2.  ; 6.
; 6. 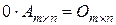 ;
;
3.  ; 7.
; 7.  ;
;
4.  ; 8.
; 8.  ;
;
9. 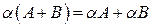 ;
;
10.  .
.
где A, B и С – матрицы одних и тех же размеров; O – нулевая матрица, (- A) – матрица, противоположная матрице A; a и b - любые действительные числа.
|
|
|
Произведение матриц
Определение 1.7. Матрицы A и B называются согласованными, если число столбцов («ширина») первой матрицы равно числу строк («высоте») второй матрицы.
Определение 1.8. Произведением матрицы  на матрицу
на матрицу 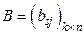 называется матрица
называется матрица  , каждый элемент которой определяется следующим образом:
, каждый элемент которой определяется следующим образом:
 . (1.5)
. (1.5)
Произведение AB рассматривают как результат умножения матрицы A на матрицу B слева или умножение матрицы B на матрицу A справа.
Пример 1.4. Найти произведения AB и BA для следующих матриц:
 и
и 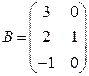 .
.
Решение. Так как матрица A имеет размерность 2´3, а матрица B – размерность 3´2, то эти матрицы согласованны и результатом произведения AB будет матрица C размерности 2´2.

 .
.
Так как матрица B имеет размерность 3´2, а матрица A - размерность 2´3, то эти матрицы согласованны и результатом произведения будет матрица D размерности 3´3.

 .
.
,
Произведение матриц можно находить с помощью программы Excel пакета Microsoft Office.
Надо отметить, что результатом произведения двух ненулевых матриц может быть нулевая матрица.
Как видно из примера 1.4. AB ¹ BA.
Определение 1.9. Если для двух матриц  и
и  выполняется равенство AB = BA, то такие матрицы называются перестановочными, или коммутативными.
выполняется равенство AB = BA, то такие матрицы называются перестановочными, или коммутативными.
Произведение матриц обладает следующими свойствами, которые примем без доказательства:
1.  , единичная матрица E играет роль единицы;
, единичная матрица E играет роль единицы;
2.  , нулевая матрица O играет роль нуля;
, нулевая матрица O играет роль нуля;
3.  ;
;
4.  ; 6.
; 6. 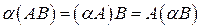 ;
;
5.  ; 7.
; 7.  .
.
где A, B и С – согласованные матрицы; a и b - любые действительные числа.
Определение 1.10. Целой положительной степенью  квадратной матрицы A называется произведение k матриц, каждая из которых равна A, т.е.
квадратной матрицы A называется произведение k матриц, каждая из которых равна A, т.е.
 . (1.6)
. (1.6)
Матрица  имеет тот же порядок, что и матрица A.
имеет тот же порядок, что и матрица A.
Нулевой степенью квадратной матрицы 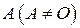 называется единичная матрица того же порядка, что и A, т.е.
называется единичная матрица того же порядка, что и A, т.е.  . Первой степенью
. Первой степенью  матрицы A называется сама матрица A, т.е.
матрицы A называется сама матрица A, т.е.  . Далее
. Далее  ,
,  и т.д.
и т.д.
|
|
|
Пример 1.5. Дана матрица  . Найти
. Найти  .
.
Решение. Согласно формулы (1.6) имеем

 .
.
,
Определение 1.11. Пусть  - некоторый многочлен степени n, тогда многочленом от матрицы A называется матрица
- некоторый многочлен степени n, тогда многочленом от матрицы A называется матрица
 , (1.7)
, (1.7)
где  − единичная матрица той же размерности, что и матрица
− единичная матрица той же размерности, что и матрица  .
.
Пусть дан многочлен  . Если
. Если  является нулевой матрицей, т.е.
является нулевой матрицей, т.е.  , то матрица A называется корнем многочлена
, то матрица A называется корнем многочлена  .
.
Пример 1.6. Найти многочлен  , если
, если  и
и  .
.
Решение. В соответствии с определением многочлена от матрицы получаем

 .,
.,
Элементарные преобразования матриц
Элементарными преобразованиями матриц являются:
- перестановка местами двух параллельных рядов матрицы;
- умножение всех элементов ряда матрицы на число, отличное от нуля;
- прибавление ко всем элементам ряда матрицы соответствующих элементов параллельного ряда, умноженных на одно и то же число.
Определение 1.12. Две матрицы A и B называются эквивалентными, если одна из них получается из другой с помощью элементарных преобразований. Записывается
A~ B.
При помощи элементарных преобразований любую матрицу можно привести к эквивалентной ей ступенчатой матрице.
Пример 1.7. Привести данную матрицу к трапециевидной:

Решение. Сначала переставим местами первую и вторую строки, т.к. первый элемент второй строки равен 1.
 ~
~
[первую строку умножаем на (-2) и складываем со второй строкой;
первую строку умножаем на 3 и складываем с четвертой строкой]
~  ~
~
[делим третью строку на 2 и переставляем вторую и третью строки местами]
~ 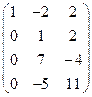 ~
~
[вторую строку умножаем на (-7) и складываем с третьей строкой;
вторую строку умножаем на 5 и складываем с четвертой строкой]
~  ~
~
[сначала разделим третью строку на 18,
а потом умножим на 21 и сложим с четвертой строкой]
~  .,
.,
2. ОПРЕДЕЛИТЕЛИ
2.1. Основные понятия
Квадратной матрице A порядка n можно сопоставить число 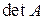 (или
(или  , или
, или  ), называемое ее определителем.
), называемое ее определителем.
Для матрицы первого порядка, т.е.  , определителем будет
, определителем будет  .
.
Определение 2.1. Определителем 2-го порядка матрицы  называется число, записанное в виде квадратной таблицы и вычисляемое, согласно указанному правилу
называется число, записанное в виде квадратной таблицы и вычисляемое, согласно указанному правилу
 . (2.1)
. (2.1)
Пример 2.1. Найти определители 2-го порядка.
|
|
|
Решение.
1)  ;
;
2)  .
.
,
Определение 2.2. Определителем 3-го порядка матрицы  называется число, записанное в виде квадратной таблицы и вычисляемое, согласно указанному правилу
называется число, записанное в виде квадратной таблицы и вычисляемое, согласно указанному правилу
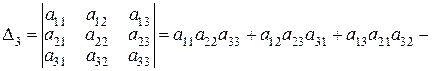
 . (2.2)
. (2.2)
Заметим, что каждое слагаемое алгебраической суммы в правой части представляет собой произведение элементов определителя, взятых по одному и только по одному из каждой строки и каждого столбца. Этому произведению приписывается соответствующий знак. Чтобы помнить, какие произведения следует брать со знаком плюс, какие – со знаком минус, можно пользоваться правилом, которое называется правилом треугольника (правило Саррюса).
Схематическое изображение правила треугольника имеет следующий вид:

«+» «-»
Пример 2.2. Найти определитель 3-го порядка.
 .
.
,
Для более удобного вычисления определителя 3-го порядка можно применить правило приписывания к определителю справа первых двух ее столбцов.
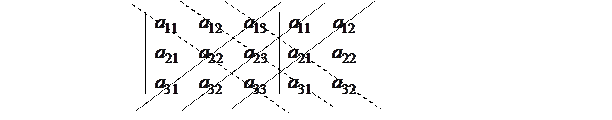
«-» «-» «-» «+» «+» «+»
Определитель матрицы A также называют детерминантом. Правило вычисления детерминанта для матрицы n -го порядка является довольно сложным для восприятия и применения. Однако известны методы, позволяющие реализовать вычисление определителей высоких порядков на основе определителей низших порядков. Один из методов основан на свойстве разложения определителя по элементам некоторого ряда (строки или столбца), который рассмотрим несколько позже. При этом заметим, что определители невысоких порядков (1-го, 2-го и 3-го) желательно вычислять согласно определению.
Определение 2.3. Минором Mij некоторого элемента  называется определитель, полученный из исходного вычеркиванием i -ой строки и j -го столбца, на пересечении которых находится выбранный элемент.
называется определитель, полученный из исходного вычеркиванием i -ой строки и j -го столбца, на пересечении которых находится выбранный элемент.
Пример 2.3. Для определителя  минор элемента
минор элемента  будет
будет  , а минор элемента
, а минор элемента  будет
будет  . Для определителя 2-го порядка
. Для определителя 2-го порядка 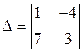 минор элемента
минор элемента  будет
будет  .
.
,
Определение 2.4. Алгебраическим дополнением Aij некоторого элемента  называется его минор, взятый со знаком
называется его минор, взятый со знаком  , т.е.
, т.е.
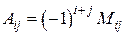 . (2.3)
. (2.3)
Пример 2.4. Для определителя  алгебраическое дополнение элемента
алгебраическое дополнение элемента  будет
будет  , а алгебраическое дополнение элемента
, а алгебраическое дополнение элемента  будет
будет  .
.
|
|
|
Каждый определитель состоит из строк и столбцов. В дальнейшем строки и столбцы будем называть рядами определителя.
Определение 2.5. Определителем матрицы n-го порядка

называется число, равное сумме произведений элементов его произвольного ряда на их алгебраические дополнения, т.е. справедлива одна из формул:
 , (2.4)
, (2.4)
называемая разложением определителя по i-ой строке, или
 , (2.5)
, (2.5)
называемая разложением определителя по j-ому столбцу.
Пример 2.5. Найти определитель 3-го порядка, используя разложение по второй строке.
 ,
,
Свойства определителей
Сформулируем основные свойства определителей, присущие определителям всех порядков. Некоторые из этих свойств докажем с использованием определителей 3-го порядка.
Свойство 1. При транспонировании значение определителя не изменяется.
Доказательство.
В определителе 3-го порядка каждую строку заменим столбцом с тем же номером, получим новый определитель.

= [полученное выражение можно сравнить с определением 2.2.] =  .
.
,
Свойство 2. Если поменять местами два параллельных ряда определителя, то он изменит знак на противоположный.
Доказательство. (Провести самостоятельно).
Свойство 3. Определитель с двумя одинаковыми параллельными рядами равен нулю.
Доказательство. (Провести самостоятельно).
Свойство 4. Если определитель содержит нулевой ряд, то его значение равно нулю.
Доказательство. (Провести самостоятельно).
Свойство 5. Если какой-либо ряд содержит общий множитель, то его можно вынести за знак определителя
Доказательство. Пусть, например, в определителе элементы второй строки имею множитель k, тогда

 ,
,
Свойство 6. Определитель, у которого элементы двух параллельных рядов соответственно пропорциональны, равен нулю.
Доказательство. (Провести самостоятельно).
Свойство 7. Если элементы какого-либо ряда определителя представляют собой сумму двух слагаемых, то определитель может быть разложен на сумму двух соответствующих определителей.
Доказательство. Пусть, например, в определителе элементы второго столбца представляют собой сумму двух слагаемых, тогда


[раскроим скобки и сгруппируем слагаемые]


 .,
.,
Свойство 8. Если к элементам какого-либо ряда определителя прибавить соответствующие элементы параллельного ряда, умноженные на одно и то же число, то его значение не изменится.
Доказательство. (Провести самостоятельно).
Свойство 9. Сумма произведений элементов какого-либо ряда определителя на алгебраические дополнения соответствующих элементов параллельного ряда равна нулю.
|
|
|
Доказательство. Покажем, например, что
 .
.



 .
.
,
|
|
|
12 |


