 |
Приложение определителей в геометрии
|
|
|
|
1. Площадь треугольника с вершинами 
, 
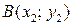и 
вычисляется по формуле:
. (2.6)
2. Условие, при котором три точки 
, 
и 
лежат на одой прямой:
. (2.7)
3. Уравнение прямой, проходящей через две точки и :
. (2.8)
4. Условие, при котором три прямые 
, 
и 
пересекаются в одной точке:
. (2.9)
Пример 2.8. Даны точки 
и 
. На прямой 
выбрать точку 
так, чтобы площадь треугольника 
была равна 4 кв.ед.
Решение. Пусть тоска имеет координаты 
и 
, т.е.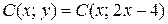 
. Сначала по формуле (2.6) находим площадь 
:
.
По условию 
. Далее получаем два уравнения:
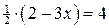или 
;
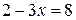или 
;
или 
.
В результате имеем две точки 
и 
.
,
3. СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
3.1. Основные понятия
Определение 3.1. Системой линейных уравнений (СЛУ), содержащей m уравнений и n неизвестных, называется система вида
(3.1)
где числа 
называются коэффициентами системы, числа 
- свободными членами.
Коэффициенты обозначаются буквой a с двумя индексами i и j; первый индекс (i) указывает номер уравнения, второй (j) – номер неизвестной, к которой относится данный коэффициент. Число m уравнений может быть больше, равно или меньше числа n неизвестных.
Определение 3.2. Решением СЛУ называется упорядоченная совокупность n чисел:
,
подстановка которых вместо 
соответственно 
обращает в тождество каждое из уравнений этой системы.
Всякое решение системы можно записать в виде матрицы-столбца
.
Допускается и такая запись: 
или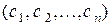 
.
Определение 3.3. СЛУ называется неоднородной, если среди свободных членов имеются отличные от нуля. Если все свободные члены равны нулю, линейная система называется однородной.
Определение 3.4. Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет ни одного решения.
|
|
|
Отметим, что однородная система всегда совместна, так как она имеет нулевое решение 
, которое называется нулевым или тривиальным.
Определение 3.5. Совместная система называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.
Решить СЛУ – это значит выяснить, совместна она или несовместна. Если система совместна, найти все ее решения.
Определение 3.6. Две системы называются эквивалентными (равносильными), если любое решение одной из них является также решением другой и обратно, т.е. если они имеют одно и то же множество решений. Любые две несовместные системы считаются эквивалентными.
Элементарными преобразованиями линейной системы называются следующие преобразования: 1) перестановка местами двух уравнений системы; 2) умножение уравнения системы на число, отличное от нуля; 3) прибавление к одному уравнению системы другого ее уравнения, умноженного на любое число, отличное от нуля.
Линейную систему можно записать в матричной форме.
Рассмотрим СЛУ:
Матрица, составленная из коэффициентов линейных уравнений системы
называется основной матрицей системы.
Матрица, полученная из основной присоединением столбца из свободных членов
называется расширенной матрицей системы.
Матрицы-столбцы, составленные из неизвестных и свободных членов имеют вид:
, 
.
Поскольку матрица A согласована с матрицей X, то можно найти произведение
.
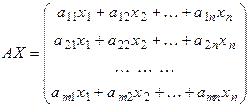Элементы этой матрицы-столбца являются левые части уравнения системы (3.1), поэтому на основании определения равенства матриц имеем:
. (3.2)
Таким образом, СЛУ (5.1) можно записать в виде одного матричного уравнения (3.2), которое называется матричной формой.
Методы решения систем линейных уравнений
Формулы Крамера
Данный метод используется только для так называемых квадратных систем уравнений, т.е. когда число уравнений равно числу неизвестных.
|
|
|
Рассмотрим систему n линейных уравнений с n неизвестными
Определитель системы обозначим 
:
.
Обозначим через 
определитель, полученный заменой в определителе 
столбца из коэффициентов при неизвестной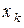 
столбцом свободных членов системы, т.е.
.
Теорема 3.1. (Теорема Крамера) Если определитель системы отличен от нуля, то система имеет единственное решение, которое находится по формулам
, (3.3)
где - определитель системы, - определитель, полученный заменой в определители системы столбца из коэффициентов при неизвестной 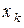столбцом свободных членов.
Данную теорему примем без доказательства.
Формулы (3.3) называются формулами Крамера.
Из теоремы Крамера следует: если однородная система имеет решение, то ее определитель равен нулю.
Пример 3.1. Решить СЛУ по формулам Крамера
Решение. Находим и определители 
:
; 
;
; 
.
Далее получаем решение:
.
,
Метод Гаусса
Метод Гаусса является исторически первым наиболее распространенным точным методом решения системы линейных уравнений. Сущность этого метода состоит в том, что посредством элементарных преобразований данная система приводится к специальному виду, из которого все решения системы непосредственно усматриваются.
Рассмотрим СЛУ (3.4), содержащую m уравнений и n неизвестных:
(3.4)
Метод Гаусса или метод последовательного исключения неизвестных, применяемый для решения системы (3.4), состоит в следующем.
Пусть в системе коэффициент 
, который называется разрешающим коэффициентом. Если 
, то на первое место можно поставить уравнение, в котором коэффициент при неизвестной 
отличен от нуля. Умножаем первое уравнение системы (3.4) на 
и прибавляем ко второму, получаем уравнение, в котором коэффициент при обращается в нуль. Умножаем первое уравнение на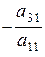 
и прибавляем к третьему, получаем уравнение, также не содержащее члена с . Аналогичным путем преобразуем все остальные уравнения. Если в 
-ом уравнении коэффициент при равен нулю, то это уравнение записываем в новую систему без изменений. В результате преобразований придем к системе, эквивалентной исходной системе уравнений:
|
|
|
(3.5)
где 
- некоторые новые коэффициенты при неизвестных, 
- новые свободные члены.
Предполагая, что 
, который становится разрешающим коэффициентом, и, оставляя неизменными первые два уравнения системы (3.5), преобразуем ее так, чтобы в каждом из остальных уравнений коэффициент при 
обратился в нуль. Продолжая этот процесс, систему (3.5) можно привести к одной из следующих систем:
1)
(3.6)
где 
и 
.
2)
(3.7)
где 
и 
.
3)
(3.8)
где 
.
Запись системы, полученной после преобразований, называют ступенчатой (в частности, при - треугольной).
Система (3.6) имеет единственное решение. Из последнего уравнения 
находим 
: 
. Из предпоследнего уравнения находим 
, затем из третьего от конца - 
. Двигаясь, таким образом, снизу вверх, найдем значения всех неизвестные.
Процесс преобразования системы (3.4) к одному из видов (3.6), (3.7) или (3.8) называют прямым ходом метода Гаусса, а описанную только что процедуру движения снизу вверх по уравнениям системы (3.6) с целью получения значений неизвестных – обратным ходом.
Система (3.7) имеет бесчисленное множество решений. Из последнего уравнения можно выразить одно из неизвестных (например, 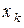) через остальные 
неизвестных (
), входящих в это уравнение. Полученное значение 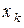подставляем в предпоследнее уравнение и находим выражение для 
через эти неизвестные и т.д. И, наконец, выражаем через . В результате система (3.7) будет приведена к виду
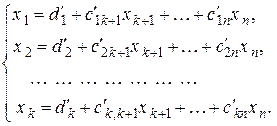(3.9)
Полученная система представляет собой общее решение исходной системы. Неизвестные , стоящие в правой части равенств, называются свободными, а 
- базисными. Свободным неизвестным можно придавать любые числовые значения и по формулам (3.9) находить соответствующие значения базисных неизвестных. Каждый раз будет получаться определенное частное решение исходной системы. Заметим, что частное решение, получаемое из общего при нулевых значениях свободных неизвестных, называются базисным решением системы, которое играет исключительную роль в математическом программировании.
Система (3.8) не имеет решений, так как эта система несовместна, т.е. никакие значения неизвестных не могут удовлетворять ее последнему уравнению.
|
|
|
Итак, метод последовательного исключения неизвестных применим к любой системе линейных уравнений. Решая систему этим методом, преобразования можно совершать не над самими уравнениями, а над расширенной матрицей.
Пример 3.2. Решить систему уравнений
Решение. Составляем расширенную матрицу:
.
Сначала поменяем местами первую и третью строки, чтобы первый элемент (для удобства) был равен 1. Этот элемент будет разрешающим.
~ 
~
[вторую и третью строки умножим на (-1)]
~ 
~ 
.
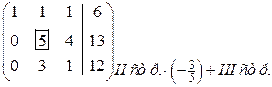По коэффициентам последней матрицы составляем систему, равносильную исходной системе:
.
Из последнего уравнения находим 
, из второго – 
и из первого – 
. Итак, исходная система имеет единственное решение 
.
,
Пример 3.3. Решить систему уравнений
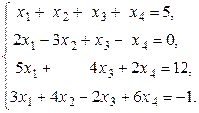
Решение. Составляем расширенную матрицу и преобразуем ее:
~ 
~ 
.
Система несовместна, так как последняя матрица содержит строку (третья строка), соответствующую уравнению, в котором все коэффициенты при неизвестных равны нулю, а свободный член отличен от нуля.
,
Пример 3.4. Решить систему уравнений
.
Решение. Составляем расширенную матрицу и преобразуем ее:
~ 
~ 
~
~ 
.
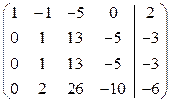Исходная система свелась к ступенчатой:
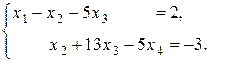
Из последнего уравнения за базисную неизвестную выберем, например, и выразим через свободные неизвестные 
: 
. Подставляем в первое уравнение и выражаем , которое становится базисной неизвестной:
.
Таким образом, получаем общее решение системы:
Пусть 
, где 
- любые действительные числа. Тогда получаем следующее решение
,
где - любые действительные числа.
,
|
|
|
12 |
